Quentin Chu
Estimating the Hallucination Rate of Generative AI
Jun 11, 2024



Abstract:This work is about estimating the hallucination rate for in-context learning (ICL) with Generative AI. In ICL, a conditional generative model (CGM) is prompted with a dataset and asked to make a prediction based on that dataset. The Bayesian interpretation of ICL assumes that the CGM is calculating a posterior predictive distribution over an unknown Bayesian model of a latent parameter and data. With this perspective, we define a \textit{hallucination} as a generated prediction that has low-probability under the true latent parameter. We develop a new method that takes an ICL problem -- that is, a CGM, a dataset, and a prediction question -- and estimates the probability that a CGM will generate a hallucination. Our method only requires generating queries and responses from the model and evaluating its response log probability. We empirically evaluate our method on synthetic regression and natural language ICL tasks using large language models.
Mixed-Curvature Decision Trees and Random Forests
Jun 07, 2024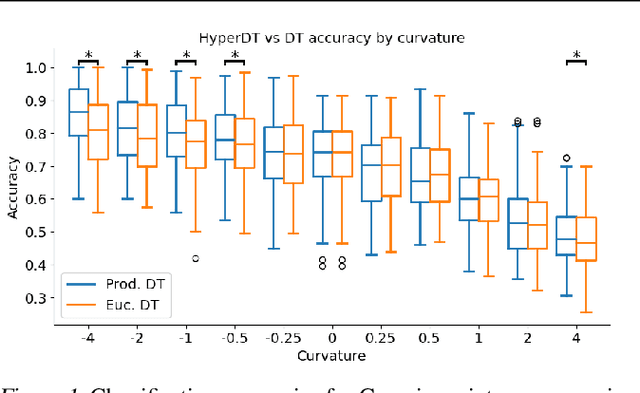

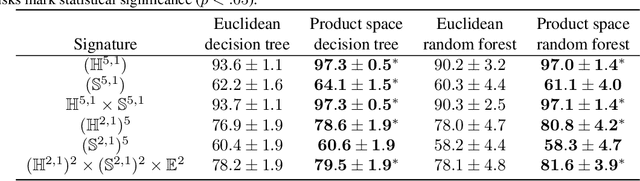
Abstract:We extend decision tree and random forest algorithms to mixed-curvature product spaces. Such spaces, defined as Cartesian products of Euclidean, hyperspherical, and hyperbolic manifolds, can often embed points from pairwise distances with much lower distortion than in single manifolds. To date, all classifiers for product spaces fit a single linear decision boundary, and no regressor has been described. Our method overcomes these limitations by enabling simple, expressive classification and regression in product manifolds. We demonstrate the superior accuracy of our tool compared to Euclidean methods operating in the ambient space for component manifolds covering a wide range of curvatures, as well as on a selection of product manifolds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge