Transcoders Find Interpretable LLM Feature Circuits

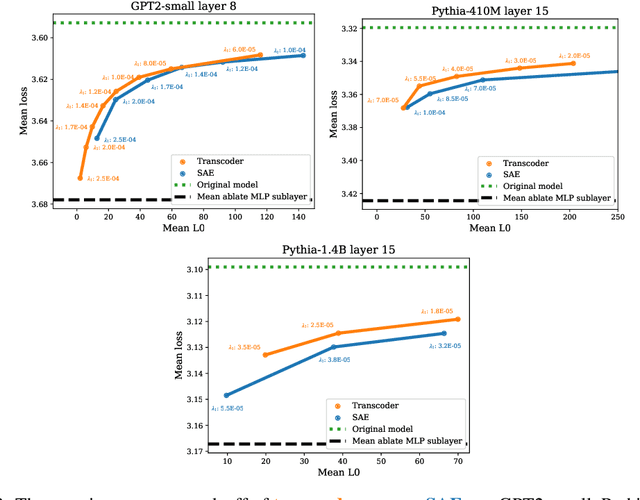
A key goal in mechanistic interpretability is circuit analysis: finding sparse subgraphs of models corresponding to specific behaviors or capabilities. However, MLP sublayers make fine-grained circuit analysis on transformer-based language models difficult. In particular, interpretable features -- such as those found by sparse autoencoders (SAEs) -- are typically linear combinations of extremely many neurons, each with its own nonlinearity to account for. Circuit analysis in this setting thus either yields intractably large circuits or fails to disentangle local and global behavior. To address this we explore transcoders, which seek to faithfully approximate a densely activating MLP layer with a wider, sparsely-activating MLP layer. We successfully train transcoders on language models with 120M, 410M, and 1.4B parameters, and find them to perform at least on par with SAEs in terms of sparsity, faithfulness, and human-interpretability. We then introduce a novel method for using transcoders to perform weights-based circuit analysis through MLP sublayers. The resulting circuits neatly factorize into input-dependent and input-invariant terms. Finally, we apply transcoders to reverse-engineer unknown circuits in the model, and we obtain novel insights regarding the greater-than circuit in GPT2-small. Our results suggest that transcoders can prove effective in decomposing model computations involving MLPs into interpretable circuits. Code is available at https://github.com/jacobdunefsky/transcoder_circuits.

Mixed-Curvature Decision Trees and Random Forests

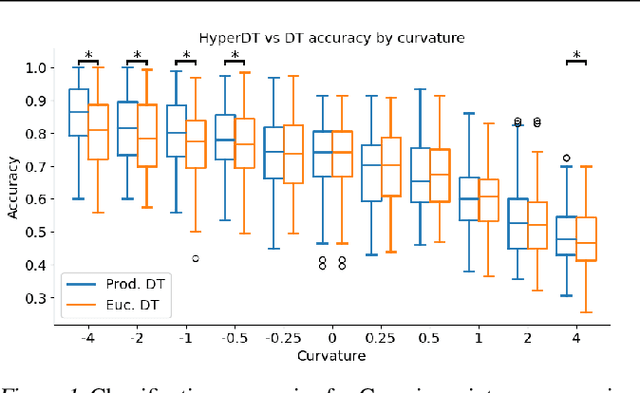
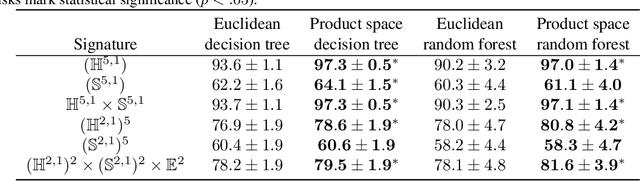
We extend decision tree and random forest algorithms to mixed-curvature product spaces. Such spaces, defined as Cartesian products of Euclidean, hyperspherical, and hyperbolic manifolds, can often embed points from pairwise distances with much lower distortion than in single manifolds. To date, all classifiers for product spaces fit a single linear decision boundary, and no regressor has been described. Our method overcomes these limitations by enabling simple, expressive classification and regression in product manifolds. We demonstrate the superior accuracy of our tool compared to Euclidean methods operating in the ambient space for component manifolds covering a wide range of curvatures, as well as on a selection of product manifolds.

Variational Pseudo Marginal Methods for Jet Reconstruction in Particle Physics

Reconstructing jets, which provide vital insights into the properties and histories of subatomic particles produced in high-energy collisions, is a main problem in data analyses in collider physics. This intricate task deals with estimating the latent structure of a jet (binary tree) and involves parameters such as particle energy, momentum, and types. While Bayesian methods offer a natural approach for handling uncertainty and leveraging prior knowledge, they face significant challenges due to the super-exponential growth of potential jet topologies as the number of observed particles increases. To address this, we introduce a Combinatorial Sequential Monte Carlo approach for inferring jet latent structures. As a second contribution, we leverage the resulting estimator to develop a variational inference algorithm for parameter learning. Building on this, we introduce a variational family using a pseudo-marginal framework for a fully Bayesian treatment of all variables, unifying the generative model with the inference process. We illustrate our method's effectiveness through experiments using data generated with a collider physics generative model, highlighting superior speed and accuracy across a range of tasks.

Fast hyperboloid decision tree algorithms

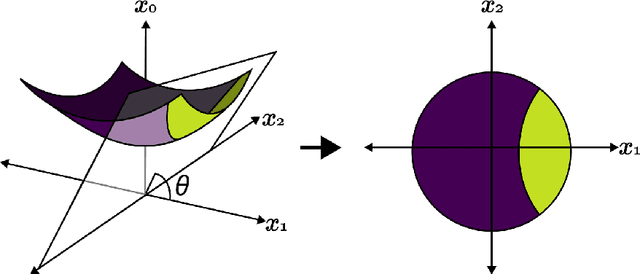
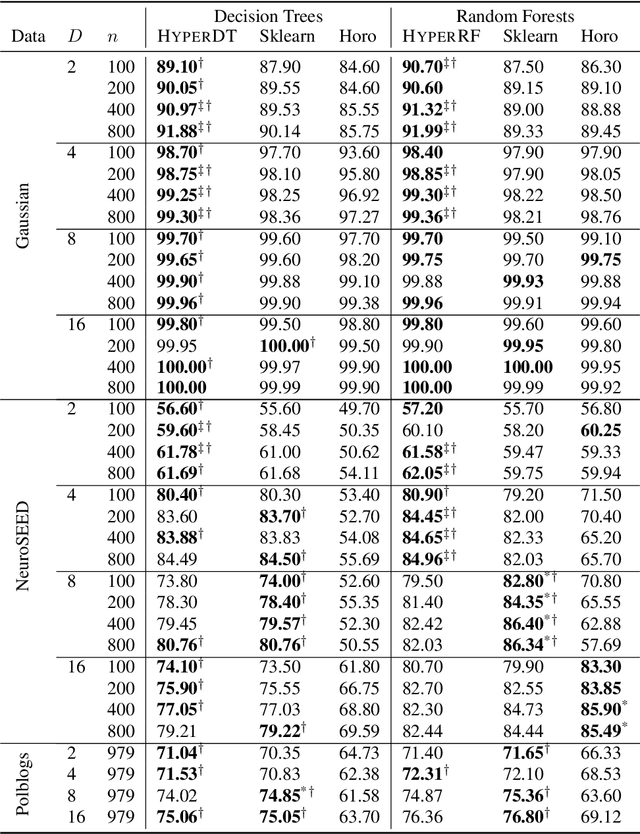
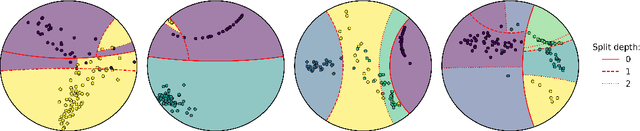
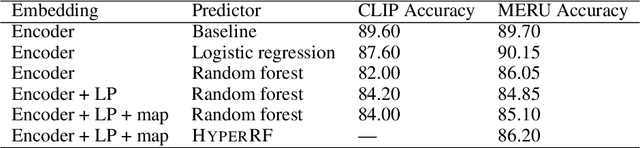
Hyperbolic geometry is gaining traction in machine learning for its effectiveness at capturing hierarchical structures in real-world data. Hyperbolic spaces, where neighborhoods grow exponentially, offer substantial advantages and consistently deliver state-of-the-art results across diverse applications. However, hyperbolic classifiers often grapple with computational challenges. Methods reliant on Riemannian optimization frequently exhibit sluggishness, stemming from the increased computational demands of operations on Riemannian manifolds. In response to these challenges, we present hyperDT, a novel extension of decision tree algorithms into hyperbolic space. Crucially, hyperDT eliminates the need for computationally intensive Riemannian optimization, numerically unstable exponential and logarithmic maps, or pairwise comparisons between points by leveraging inner products to adapt Euclidean decision tree algorithms to hyperbolic space. Our approach is conceptually straightforward and maintains constant-time decision complexity while mitigating the scalability issues inherent in high-dimensional Euclidean spaces. Building upon hyperDT we introduce hyperRF, a hyperbolic random forest model. Extensive benchmarking across diverse datasets underscores the superior performance of these models, providing a swift, precise, accurate, and user-friendly toolkit for hyperbolic data analysis.