Variational Pseudo Marginal Methods for Jet Reconstruction in Particle Physics

Reconstructing jets, which provide vital insights into the properties and histories of subatomic particles produced in high-energy collisions, is a main problem in data analyses in collider physics. This intricate task deals with estimating the latent structure of a jet (binary tree) and involves parameters such as particle energy, momentum, and types. While Bayesian methods offer a natural approach for handling uncertainty and leveraging prior knowledge, they face significant challenges due to the super-exponential growth of potential jet topologies as the number of observed particles increases. To address this, we introduce a Combinatorial Sequential Monte Carlo approach for inferring jet latent structures. As a second contribution, we leverage the resulting estimator to develop a variational inference algorithm for parameter learning. Building on this, we introduce a variational family using a pseudo-marginal framework for a fully Bayesian treatment of all variables, unifying the generative model with the inference process. We illustrate our method's effectiveness through experiments using data generated with a collider physics generative model, highlighting superior speed and accuracy across a range of tasks.

Variational Combinatorial Sequential Monte Carlo Methods for Bayesian Phylogenetic Inference

Bayesian phylogenetic inference is often conducted via local or sequential search over topologies and branch lengths using algorithms such as random-walk Markov chain Monte Carlo (MCMC) or Combinatorial Sequential Monte Carlo (CSMC). However, when MCMC is used for evolutionary parameter learning, convergence requires long runs with inefficient exploration of the state space. We introduce Variational Combinatorial Sequential Monte Carlo (VCSMC), a powerful framework that establishes variational sequential search to learn distributions over intricate combinatorial structures. We then develop nested CSMC, an efficient proposal distribution for CSMC and prove that nested CSMC is an exact approximation to the (intractable) locally optimal proposal. We use nested CSMC to define a second objective, VNCSMC which yields tighter lower bounds than VCSMC. We show that VCSMC and VNCSMC are computationally efficient and explore higher probability spaces than existing methods on a range of tasks.

AutoML using Metadata Language Embeddings

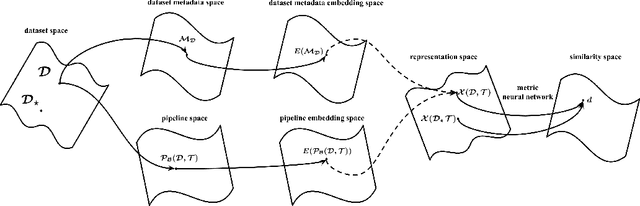
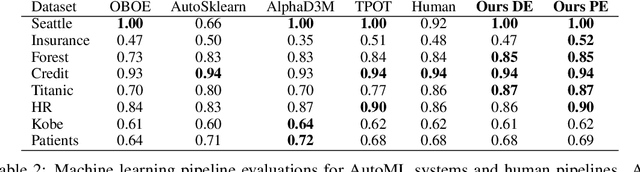
As a human choosing a supervised learning algorithm, it is natural to begin by reading a text description of the dataset and documentation for the algorithms you might use. We demonstrate that the same idea improves the performance of automated machine learning methods. We use language embeddings from modern NLP to improve state-of-the-art AutoML systems by augmenting their recommendations with vector embeddings of datasets and of algorithms. We use these embeddings in a neural architecture to learn the distance between best-performing pipelines. The resulting (meta-)AutoML framework improves on the performance of existing AutoML frameworks. Our zero-shot AutoML system using dataset metadata embeddings provides good solutions instantaneously, running in under one second of computation. Performance is competitive with AutoML systems OBOE, AutoSklearn, AlphaD3M, and TPOT when each framework is allocated a minute of computation. We make our data, models, and code publicly available.

Particle Smoothing Variational Objectives

A body of recent work has focused on constructing a variational family of filtered distributions using Sequential Monte Carlo (SMC). Inspired by this work, we introduce Particle Smoothing Variational Objectives (SVO), a novel backward simulation technique and smoothed approximate posterior defined through a subsampling process. SVO augments support of the proposal and boosts particle diversity. Recent literature argues that increasing the number of samples K to obtain tighter variational bounds may hurt the proposal learning, due to a signal-to-noise ratio (SNR) of gradient estimators decreasing at the rate $\mathcal{O}(1/\sqrt{K})$. As a second contribution, we develop theoretical and empirical analysis of the SNR in filtering SMC, which motivates our choice of biased gradient estimators. We prove that introducing bias by dropping Categorical terms from the gradient estimate or using Gumbel-Softmax mitigates the adverse effect on the SNR. We apply SVO to three nonlinear latent dynamics tasks and provide statistics to rigorously quantify the predictions of filtered and smoothed objectives. SVO consistently outperforms filtered objectives when given fewer Monte Carlo samples on three nonlinear systems of increasing complexity.

A Novel Variational Family for Hidden Nonlinear Markov Models

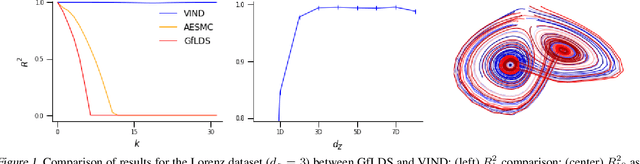
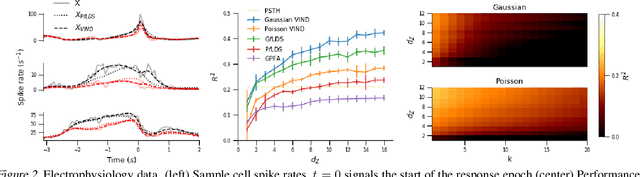
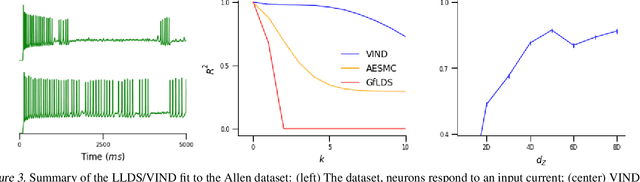
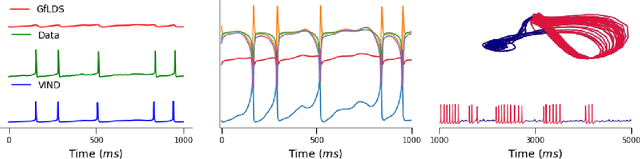
Latent variable models have been widely applied for the analysis and visualization of large datasets. In the case of sequential data, closed-form inference is possible when the transition and observation functions are linear. However, approximate inference techniques are usually necessary when dealing with nonlinear dynamics and observation functions. Here, we propose a novel variational inference framework for the explicit modeling of time series, Variational Inference for Nonlinear Dynamics (VIND), that is able to uncover nonlinear observation and transition functions from sequential data. The framework includes a structured approximate posterior, and an algorithm that relies on the fixed-point iteration method to find the best estimate for latent trajectories. We apply the method to several datasets and show that it is able to accurately infer the underlying dynamics of these systems, in some cases substantially outperforming state-of-the-art methods.