Variational Pseudo Marginal Methods for Jet Reconstruction in Particle Physics

Reconstructing jets, which provide vital insights into the properties and histories of subatomic particles produced in high-energy collisions, is a main problem in data analyses in collider physics. This intricate task deals with estimating the latent structure of a jet (binary tree) and involves parameters such as particle energy, momentum, and types. While Bayesian methods offer a natural approach for handling uncertainty and leveraging prior knowledge, they face significant challenges due to the super-exponential growth of potential jet topologies as the number of observed particles increases. To address this, we introduce a Combinatorial Sequential Monte Carlo approach for inferring jet latent structures. As a second contribution, we leverage the resulting estimator to develop a variational inference algorithm for parameter learning. Building on this, we introduce a variational family using a pseudo-marginal framework for a fully Bayesian treatment of all variables, unifying the generative model with the inference process. We illustrate our method's effectiveness through experiments using data generated with a collider physics generative model, highlighting superior speed and accuracy across a range of tasks.

Exact and Approximate Hierarchical Clustering Using A*

Hierarchical clustering is a critical task in numerous domains. Many approaches are based on heuristics and the properties of the resulting clusterings are studied post hoc. However, in several applications, there is a natural cost function that can be used to characterize the quality of the clustering. In those cases, hierarchical clustering can be seen as a combinatorial optimization problem. To that end, we introduce a new approach based on A* search. We overcome the prohibitively large search space by combining A* with a novel \emph{trellis} data structure. This combination results in an exact algorithm that scales beyond previous state of the art, from a search space with $10^{12}$ trees to $10^{15}$ trees, and an approximate algorithm that improves over baselines, even in enormous search spaces that contain more than $10^{1000}$ trees. We empirically demonstrate that our method achieves substantially higher quality results than baselines for a particle physics use case and other clustering benchmarks. We describe how our method provides significantly improved theoretical bounds on the time and space complexity of A* for clustering.

Hierarchical clustering in particle physics through reinforcement learning

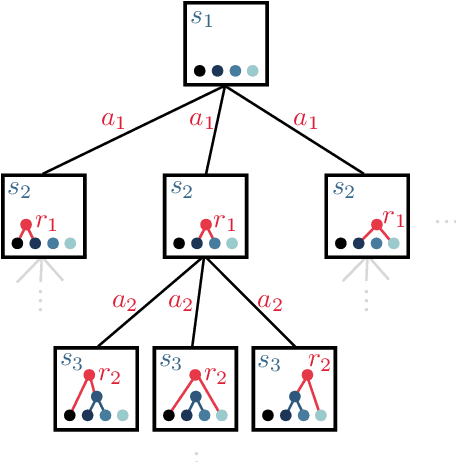
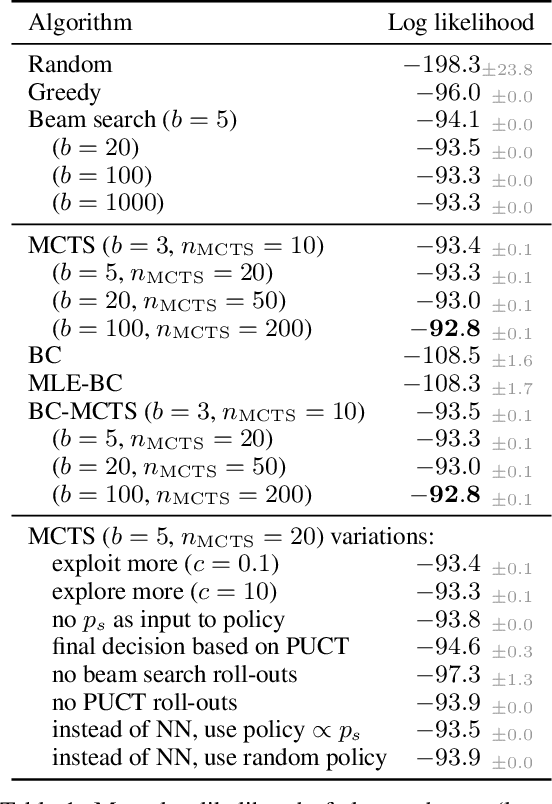
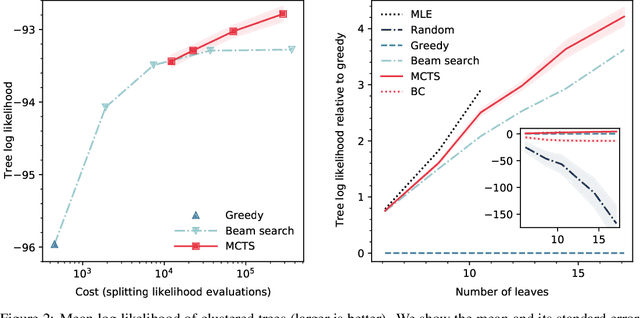
Particle physics experiments often require the reconstruction of decay patterns through a hierarchical clustering of the observed final-state particles. We show that this task can be phrased as a Markov Decision Process and adapt reinforcement learning algorithms to solve it. In particular, we show that Monte-Carlo Tree Search guided by a neural policy can construct high-quality hierarchical clusterings and outperform established greedy and beam search baselines.

Compact Representation of Uncertainty in Hierarchical Clustering

Hierarchical clustering is a fundamental task often used to discover meaningful structures in data, such as phylogenetic trees, taxonomies of concepts, subtypes of cancer, and cascades of particle decays in particle physics. When multiple hierarchical clusterings of the data are possible, it is useful to represent uncertainty in the clustering through various probabilistic quantities. Existing approaches represent uncertainty for a range of models; however, they only provide approximate inference. This paper presents dynamic-programming algorithms and proofs for exact inference in hierarchical clustering. We are able to compute the partition function, MAP hierarchical clustering, and marginal probabilities of sub-hierarchies and clusters. Our method supports a wide range of hierarchical models and only requires a cluster compatibility function. Rather than scaling with the number of hierarchical clusterings of $n$ elements ($\omega(n n! / 2^{n-1})$), our approach runs in time and space proportional to the significantly smaller powerset of $n$. Despite still being large, these algorithms enable exact inference in small-data applications and are also interesting from a theoretical perspective. We demonstrate the utility of our method and compare its performance with respect to existing approximate methods.