Maximum a Posteriori Inference for Factor Graphs via Benders' Decomposition

Many Bayesian statistical inference problems come down to computing a maximum a-posteriori (MAP) assignment of latent variables. Yet, standard methods for estimating the MAP assignment do not have a finite time guarantee that the algorithm has converged to a fixed point. Previous research has found that MAP inference can be represented in dual form as a linear programming problem with a non-polynomial number of constraints. A Lagrangian relaxation of the dual yields a statistical inference algorithm as a linear programming problem. However, the decision as to which constraints to remove in the relaxation is often heuristic. We present a method for maximum a-posteriori inference in general Bayesian factor models that sequentially adds constraints to the fully relaxed dual problem using Benders' decomposition. Our method enables the incorporation of expressive integer and logical constraints in clustering problems such as must-link, cannot-link, and a minimum number of whole samples allocated to each cluster. Using this approach, we derive MAP estimation algorithms for the Bayesian Gaussian mixture model and latent Dirichlet allocation. Empirical results show that our method produces a higher optimal posterior value compared to Gibbs sampling and variational Bayes methods for standard data sets and provides certificate of convergence.

Cost-aware Generalized $α$-investing for Multiple Hypothesis Testing

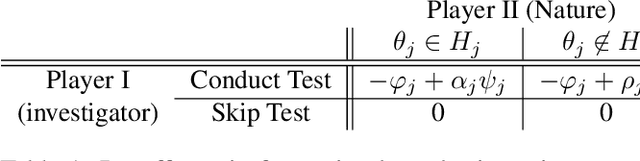
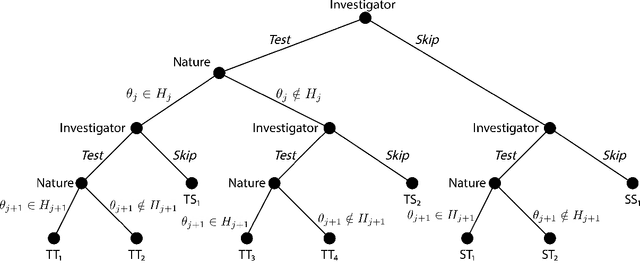
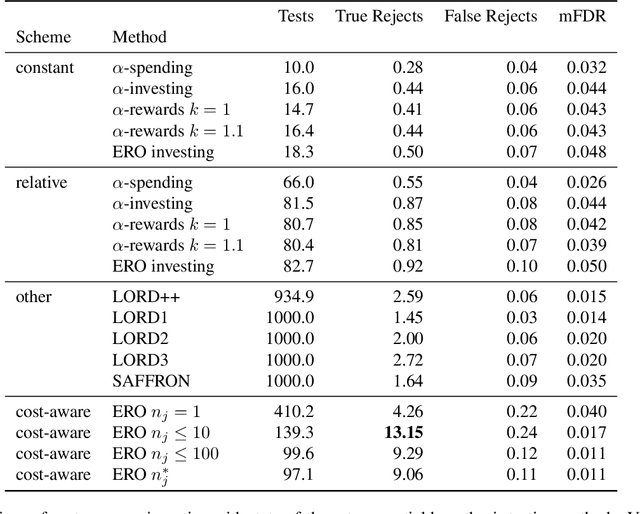
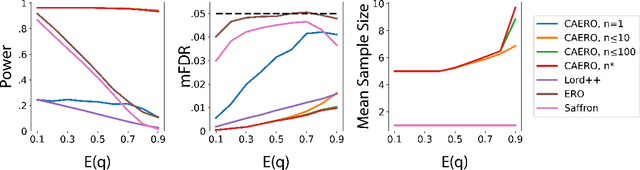
We consider the problem of sequential multiple hypothesis testing with nontrivial data collection cost. This problem appears, for example, when conducting biological experiments to identify differentially expressed genes in a disease process. This work builds on the generalized $\alpha$-investing framework that enables control of the false discovery rate in a sequential testing setting. We make a theoretical analysis of the long term asymptotic behavior of $\alpha$-wealth which motivates a consideration of sample size in the $\alpha$-investing decision rule. Using the game theoretic principle of indifference, we construct a decision rule that optimizes the expected return (ERO) of $\alpha$-wealth and provides an optimal sample size for the test. We show empirical results that a cost-aware ERO decision rule correctly rejects more false null hypotheses than other methods. We extend cost-aware ERO investing to finite-horizon testing which enables the decision rule to hedge against the risk of unproductive tests. Finally, empirical tests on a real data set from a biological experiment show that cost-aware ERO produces actionable decisions as to which tests to conduct and if so at what sample size.

Doubly Non-Central Beta Matrix Factorization for DNA Methylation Data

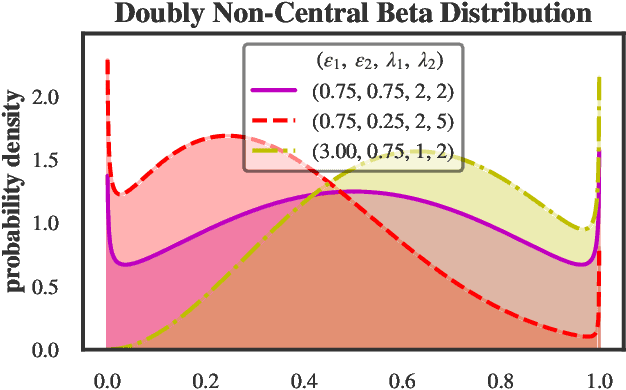
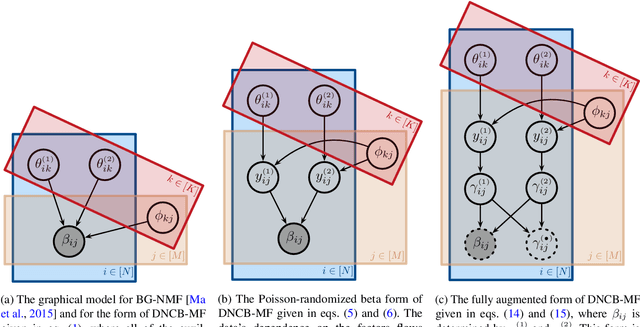
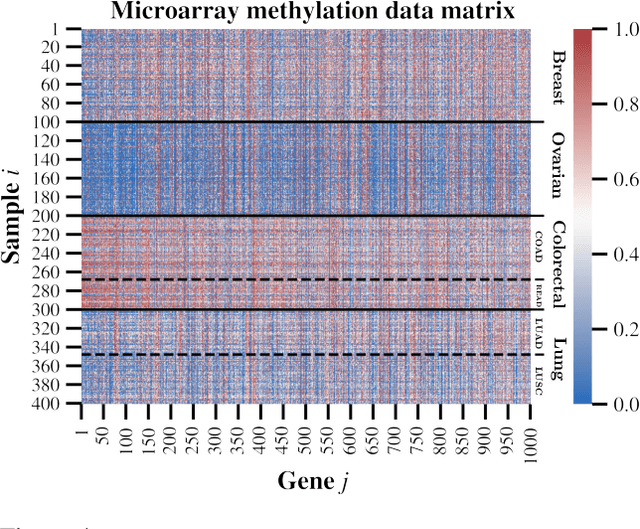
We present a new non-negative matrix factorization model for $(0,1)$ bounded-support data based on the doubly non-central beta (DNCB) distribution, a generalization of the beta distribution. The expressiveness of the DNCB distribution is particularly useful for modeling DNA methylation datasets, which are typically highly dispersed and multi-modal; however, the model structure is sufficiently general that it can be adapted to many other domains where latent representations of $(0,1)$ bounded-support data are of interest. Although the DNCB distribution lacks a closed-form conjugate prior, several augmentations let us derive an efficient posterior inference algorithm composed entirely of analytic updates. Our model improves out-of-sample predictive performance on both real and synthetic DNA methylation datasets over state-of-the-art methods in bioinformatics. In addition, our model yields meaningful latent representations that accord with existing biological knowledge.

Exact and Approximate Hierarchical Clustering Using A*

Hierarchical clustering is a critical task in numerous domains. Many approaches are based on heuristics and the properties of the resulting clusterings are studied post hoc. However, in several applications, there is a natural cost function that can be used to characterize the quality of the clustering. In those cases, hierarchical clustering can be seen as a combinatorial optimization problem. To that end, we introduce a new approach based on A* search. We overcome the prohibitively large search space by combining A* with a novel \emph{trellis} data structure. This combination results in an exact algorithm that scales beyond previous state of the art, from a search space with $10^{12}$ trees to $10^{15}$ trees, and an approximate algorithm that improves over baselines, even in enormous search spaces that contain more than $10^{1000}$ trees. We empirically demonstrate that our method achieves substantially higher quality results than baselines for a particle physics use case and other clustering benchmarks. We describe how our method provides significantly improved theoretical bounds on the time and space complexity of A* for clustering.

Compact Representation of Uncertainty in Hierarchical Clustering

Hierarchical clustering is a fundamental task often used to discover meaningful structures in data, such as phylogenetic trees, taxonomies of concepts, subtypes of cancer, and cascades of particle decays in particle physics. When multiple hierarchical clusterings of the data are possible, it is useful to represent uncertainty in the clustering through various probabilistic quantities. Existing approaches represent uncertainty for a range of models; however, they only provide approximate inference. This paper presents dynamic-programming algorithms and proofs for exact inference in hierarchical clustering. We are able to compute the partition function, MAP hierarchical clustering, and marginal probabilities of sub-hierarchies and clusters. Our method supports a wide range of hierarchical models and only requires a cluster compatibility function. Rather than scaling with the number of hierarchical clusterings of $n$ elements ($\omega(n n! / 2^{n-1})$), our approach runs in time and space proportional to the significantly smaller powerset of $n$. Despite still being large, these algorithms enable exact inference in small-data applications and are also interesting from a theoretical perspective. We demonstrate the utility of our method and compare its performance with respect to existing approximate methods.

Maximum a-Posteriori Estimation for the Gaussian Mixture Model via Mixed Integer Nonlinear Programming

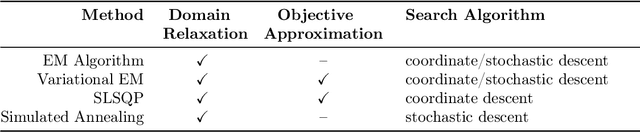
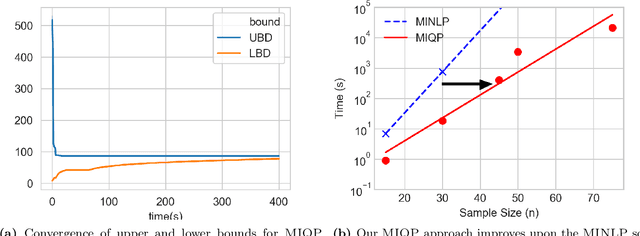
We present a global optimization approach for solving the classical maximum a-posteriori (MAP) estimation problem for the Gaussian mixture model. Our approach formulates the MAP estimation problem as a mixed-integer nonlinear optimization problem (MINLP). Our method provides a certificate of global optimality, can accommodate side constraints, and is extendable to other finite mixture models. We propose an approximation to the MINLP hat transforms it into a mixed integer quadratic program (MIQP) which preserves global optimality within desired accuracy and improves computational aspects. Numerical experiments compare our method to standard estimation approaches and show that our method finds the globally optimal MAP for some standard data sets, providing a benchmark for comparing estimation methods.

A Deterministic Global Optimization Method for Variational Inference

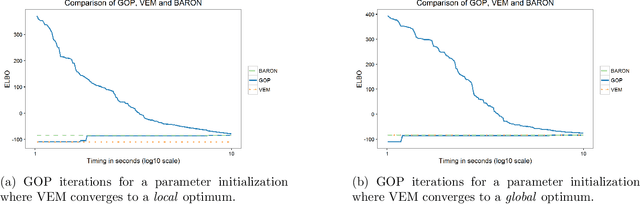
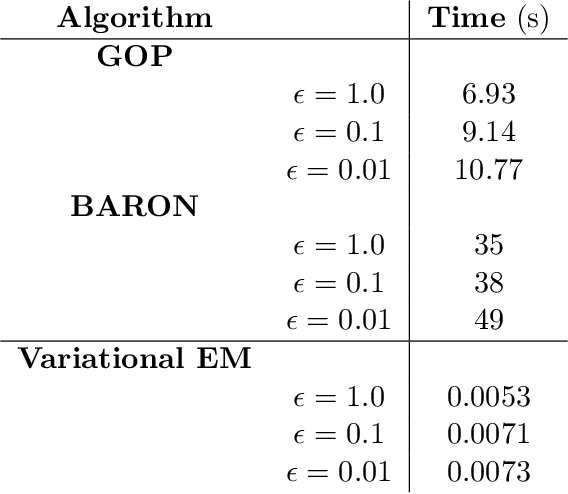
Variational inference methods for latent variable statistical models have gained popularity because they are relatively fast, can handle large data sets, and have deterministic convergence guarantees. However, in practice it is unclear whether the fixed point identified by the variational inference algorithm is a local or a global optimum. Here, we propose a method for constructing iterative optimization algorithms for variational inference problems that are guaranteed to converge to the $\epsilon$-global variational lower bound on the log-likelihood. We derive inference algorithms for two variational approximations to a standard Bayesian Gaussian mixture model (BGMM). We present a minimal data set for empirically testing convergence and show that a variational inference algorithm frequently converges to a local optimum while our algorithm always converges to the globally optimal variational lower bound. We characterize the loss incurred by choosing a non-optimal variational approximation distribution suggesting that selection of the approximating variational distribution deserves as much attention as the selection of the original statistical model for a given data set.

A global optimization algorithm for sparse mixed membership matrix factorization

Mixed membership factorization is a popular approach for analyzing data sets that have within-sample heterogeneity. In recent years, several algorithms have been developed for mixed membership matrix factorization, but they only guarantee estimates from a local optimum. Here, we derive a global optimization (GOP) algorithm that provides a guaranteed $\epsilon$-global optimum for a sparse mixed membership matrix factorization problem. We test the algorithm on simulated data and find the algorithm always bounds the global optimum across random initializations and explores multiple modes efficiently.

Variational inference for rare variant detection in deep, heterogeneous next-generation sequencing data

The detection of rare variants is important for understanding the genetic heterogeneity in mixed samples. Recently, next-generation sequencing (NGS) technologies have enabled the identification of single nucleotide variants (SNVs) in mixed samples with high resolution. Yet, the noise inherent in the biological processes involved in next-generation sequencing necessitates the use of statistical methods to identify true rare variants. We propose a novel Bayesian statistical model and a variational expectation-maximization (EM) algorithm to estimate non-reference allele frequency (NRAF) and identify SNVs in heterogeneous cell populations. We demonstrate that our variational EM algorithm has comparable sensitivity and specificity compared with a Markov Chain Monte Carlo (MCMC) sampling inference algorithm, and is more computationally efficient on tests of low coverage ($27\times$ and $298\times$) data. Furthermore, we show that our model with a variational EM inference algorithm has higher specificity than many state-of-the-art algorithms. In an analysis of a directed evolution longitudinal yeast data set, we are able to identify a time-series trend in non-reference allele frequency and detect novel variants that have not yet been reported. Our model also detects the emergence of a beneficial variant earlier than was previously shown, and a pair of concomitant variants.