Pitchaya Wiratchotisatian
Maximum a-Posteriori Estimation for the Gaussian Mixture Model via Mixed Integer Nonlinear Programming
Nov 08, 2019
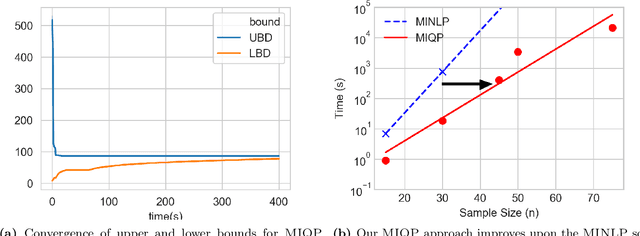

Abstract:We present a global optimization approach for solving the classical maximum a-posteriori (MAP) estimation problem for the Gaussian mixture model. Our approach formulates the MAP estimation problem as a mixed-integer nonlinear optimization problem (MINLP). Our method provides a certificate of global optimality, can accommodate side constraints, and is extendable to other finite mixture models. We propose an approximation to the MINLP hat transforms it into a mixed integer quadratic program (MIQP) which preserves global optimality within desired accuracy and improves computational aspects. Numerical experiments compare our method to standard estimation approaches and show that our method finds the globally optimal MAP for some standard data sets, providing a benchmark for comparing estimation methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge