DiversiTree: Computing Diverse Sets of Near-Optimal Solutions to Mixed-Integer Optimization Problems

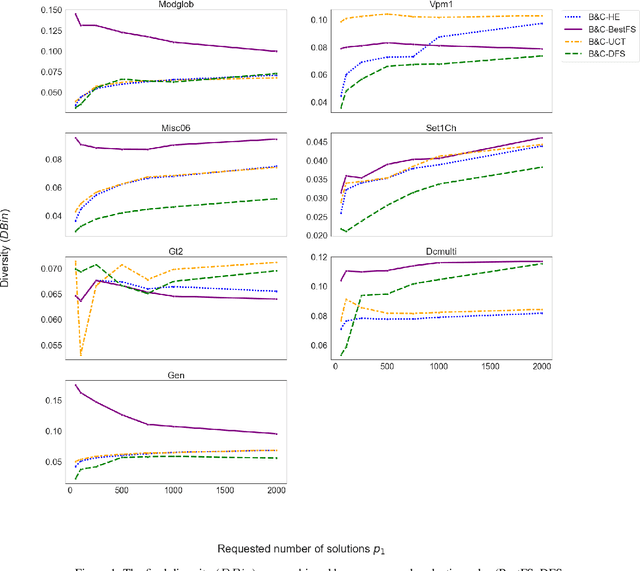
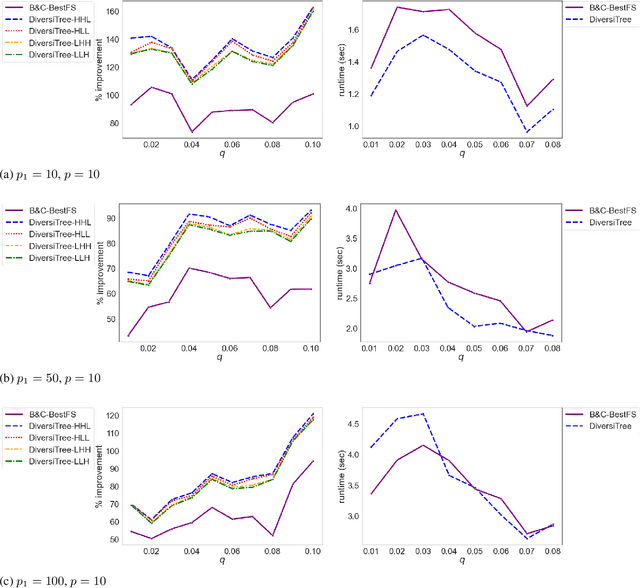
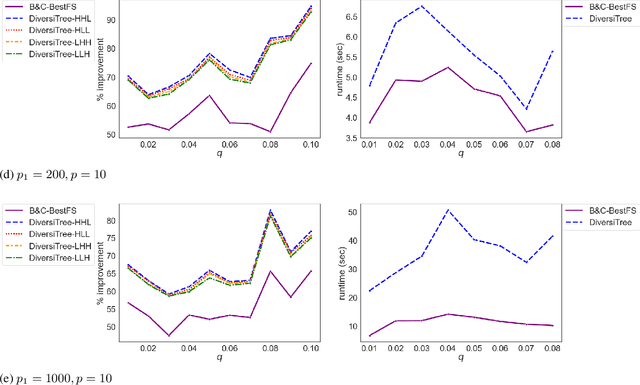
While most methods for solving mixed-integer optimization problems seek a single optimal solution, finding a diverse set of near-optimal solutions can often be more useful. State of the art methods for generating diverse near-optimal solutions usually take a two-phase approach, first finding a set of near-optimal solutions and then finding a diverse subset. In contrast, we present a method of finding a set of diverse solutions by emphasizing diversity within the search for near-optimal solutions. Specifically, within a branch-and-bound framework, we investigate parameterized node selection rules that explicitly consider diversity. Our results indicate that our approach significantly increases diversity of the final solution set. When compared with existing methods for finding diverse near-optimal sets, our method runs with similar run-time as regular node selection methods and gives a diversity improvement of up to 140%. In contrast, popular node selection rules such as best-first search gives an improvement of no more than 40%. Further, we find that our method is most effective when diversity is emphasized more in node selection when deeper in the tree and when the solution set has grown large enough.

Maximum a-Posteriori Estimation for the Gaussian Mixture Model via Mixed Integer Nonlinear Programming

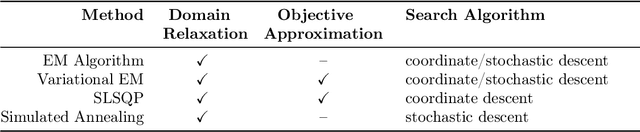
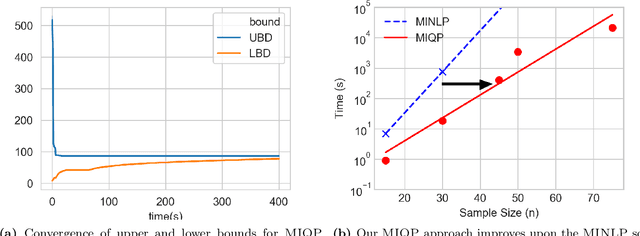
We present a global optimization approach for solving the classical maximum a-posteriori (MAP) estimation problem for the Gaussian mixture model. Our approach formulates the MAP estimation problem as a mixed-integer nonlinear optimization problem (MINLP). Our method provides a certificate of global optimality, can accommodate side constraints, and is extendable to other finite mixture models. We propose an approximation to the MINLP hat transforms it into a mixed integer quadratic program (MIQP) which preserves global optimality within desired accuracy and improves computational aspects. Numerical experiments compare our method to standard estimation approaches and show that our method finds the globally optimal MAP for some standard data sets, providing a benchmark for comparing estimation methods.

A Deterministic Global Optimization Method for Variational Inference

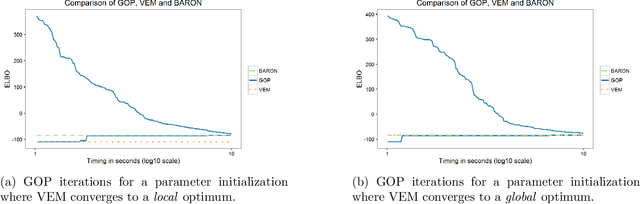
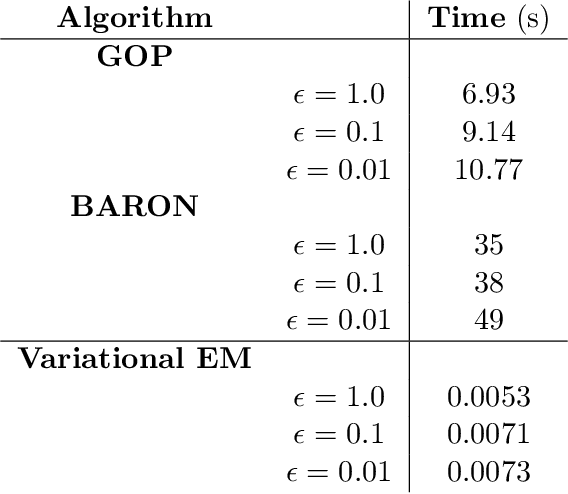
Variational inference methods for latent variable statistical models have gained popularity because they are relatively fast, can handle large data sets, and have deterministic convergence guarantees. However, in practice it is unclear whether the fixed point identified by the variational inference algorithm is a local or a global optimum. Here, we propose a method for constructing iterative optimization algorithms for variational inference problems that are guaranteed to converge to the $\epsilon$-global variational lower bound on the log-likelihood. We derive inference algorithms for two variational approximations to a standard Bayesian Gaussian mixture model (BGMM). We present a minimal data set for empirically testing convergence and show that a variational inference algorithm frequently converges to a local optimum while our algorithm always converges to the globally optimal variational lower bound. We characterize the loss incurred by choosing a non-optimal variational approximation distribution suggesting that selection of the approximating variational distribution deserves as much attention as the selection of the original statistical model for a given data set.