A Primer on Causality in Data Science

Many questions in Data Science are fundamentally causal in that our objective is to learn the effect of some exposure (randomized or not) on an outcome interest. Even studies that are seemingly non-causal (e.g. prediction or prevalence estimation) have causal elements, such as differential censoring or measurement. As a result, we, as Data Scientists, need to consider the underlying causal mechanisms that gave rise to the data, rather than simply the pattern or association observed in the data. In this work, we review the "Causal Roadmap", a formal framework to augment our traditional statistical analyses in an effort to answer the causal questions driving our research. Specific steps of the Roadmap include clearly stating the scientific question, defining of the causal model, translating the scientific question into a causal parameter, assessing the assumptions needed to translate the causal parameter into a statistical estimand, implementation of statistical estimators including parametric and semi-parametric methods, and interpretation of our findings. Throughout we focus on the effect of an exposure occurring at a single time point and provide extensions to more advanced settings.

A Deterministic Global Optimization Method for Variational Inference

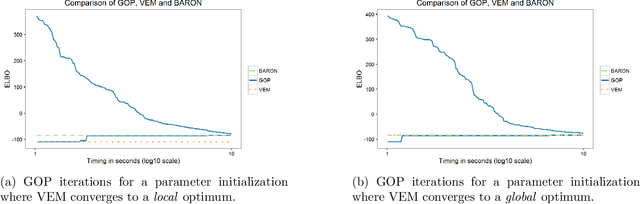
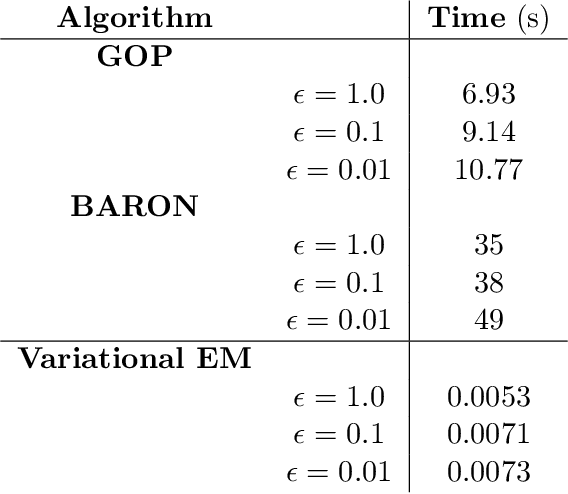
Variational inference methods for latent variable statistical models have gained popularity because they are relatively fast, can handle large data sets, and have deterministic convergence guarantees. However, in practice it is unclear whether the fixed point identified by the variational inference algorithm is a local or a global optimum. Here, we propose a method for constructing iterative optimization algorithms for variational inference problems that are guaranteed to converge to the $\epsilon$-global variational lower bound on the log-likelihood. We derive inference algorithms for two variational approximations to a standard Bayesian Gaussian mixture model (BGMM). We present a minimal data set for empirically testing convergence and show that a variational inference algorithm frequently converges to a local optimum while our algorithm always converges to the globally optimal variational lower bound. We characterize the loss incurred by choosing a non-optimal variational approximation distribution suggesting that selection of the approximating variational distribution deserves as much attention as the selection of the original statistical model for a given data set.