Cost-aware Generalized $α$-investing for Multiple Hypothesis Testing

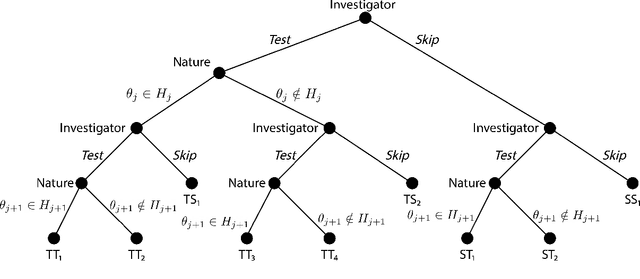
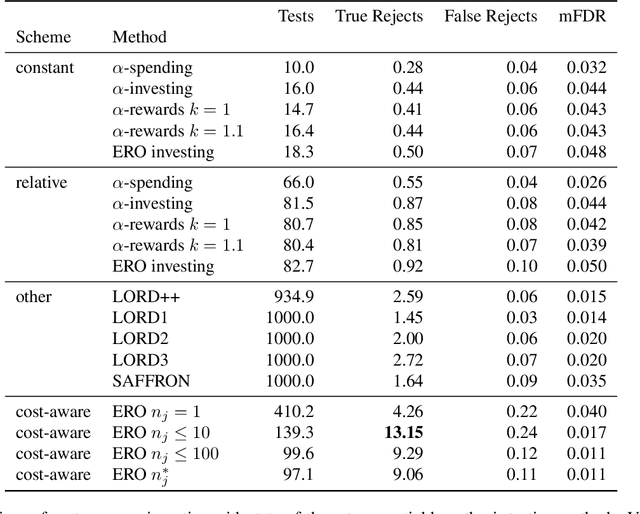
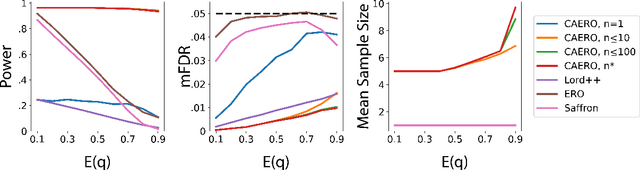
We consider the problem of sequential multiple hypothesis testing with nontrivial data collection cost. This problem appears, for example, when conducting biological experiments to identify differentially expressed genes in a disease process. This work builds on the generalized $\alpha$-investing framework that enables control of the false discovery rate in a sequential testing setting. We make a theoretical analysis of the long term asymptotic behavior of $\alpha$-wealth which motivates a consideration of sample size in the $\alpha$-investing decision rule. Using the game theoretic principle of indifference, we construct a decision rule that optimizes the expected return (ERO) of $\alpha$-wealth and provides an optimal sample size for the test. We show empirical results that a cost-aware ERO decision rule correctly rejects more false null hypotheses than other methods. We extend cost-aware ERO investing to finite-horizon testing which enables the decision rule to hedge against the risk of unproductive tests. Finally, empirical tests on a real data set from a biological experiment show that cost-aware ERO produces actionable decisions as to which tests to conduct and if so at what sample size.