Monty Hall and Optimized Conformal Prediction to Improve Decision-Making with LLMs

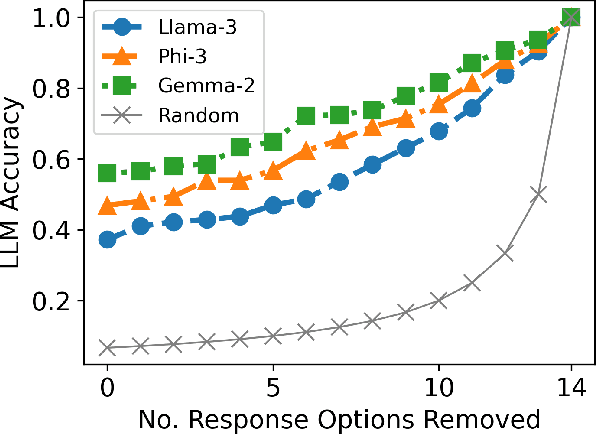
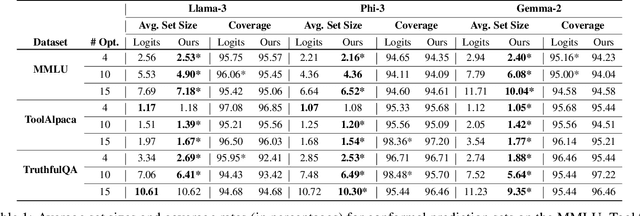
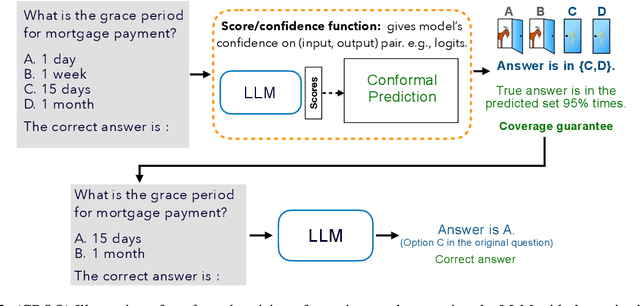
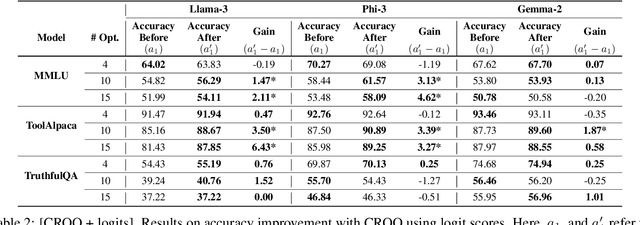
Large language models (LLMs) are empowering decision-making in several applications, including tool or API usage and answering multiple-choice questions (MCQs). However, they often make overconfident, incorrect predictions, which can be risky in high-stakes settings like healthcare and finance. To mitigate these risks, recent works have used conformal prediction (CP), a model-agnostic framework for distribution-free uncertainty quantification. CP transforms a \emph{score function} into prediction sets that contain the true answer with high probability. While CP provides this coverage guarantee for arbitrary scores, the score quality significantly impacts prediction set sizes. Prior works have relied on LLM logits or other heuristic scores, lacking quality guarantees. We address this limitation by introducing CP-OPT, an optimization framework to learn scores that minimize set sizes while maintaining coverage. Furthermore, inspired by the Monty Hall problem, we extend CP's utility beyond uncertainty quantification to improve accuracy. We propose \emph{conformal revision of questions} (CROQ) to revise the problem by narrowing down the available choices to those in the prediction set. The coverage guarantee of CP ensures that the correct choice is in the revised question prompt with high probability, while the smaller number of choices increases the LLM's chances of answering it correctly. Experiments on MMLU, ToolAlpaca, and TruthfulQA datasets with Gemma-2, Llama-3 and Phi-3 models show that CP-OPT significantly reduces set sizes while maintaining coverage, and CROQ improves accuracy over the standard inference, especially when paired with CP-OPT scores. Together, CP-OPT and CROQ offer a robust framework for improving both the safety and accuracy of LLM-driven decision-making.

Semiparametric Efficient Inference in Adaptive Experiments

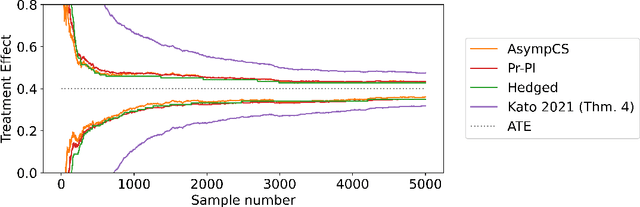
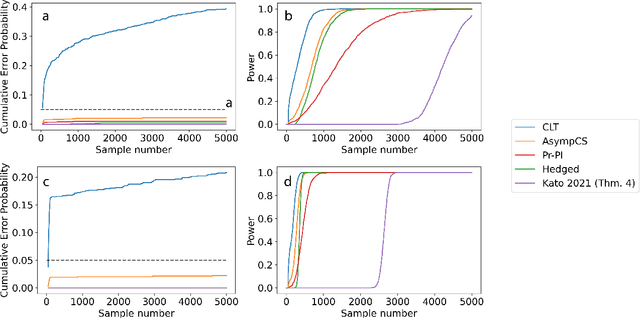
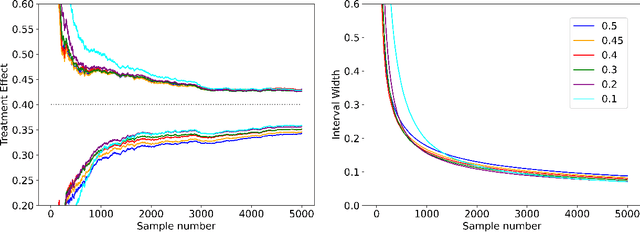
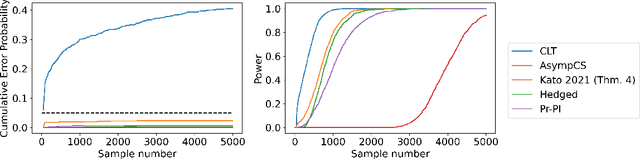
We consider the problem of efficient inference of the Average Treatment Effect in a sequential experiment where the policy governing the assignment of subjects to treatment or control can change over time. We first provide a central limit theorem for the Adaptive Augmented Inverse-Probability Weighted estimator, which is semiparametric efficient, under weaker assumptions than those previously made in the literature. This central limit theorem enables efficient inference at fixed sample sizes. We then consider a sequential inference setting, deriving both asymptotic and nonasymptotic confidence sequences that are considerably tighter than previous methods. These anytime-valid methods enable inference under data-dependent stopping times (sample sizes). Additionally, we use propensity score truncation techniques from the recent off-policy estimation literature to reduce the finite sample variance of our estimator without affecting the asymptotic variance. Empirical results demonstrate that our methods yield narrower confidence sequences than those previously developed in the literature while maintaining time-uniform error control.

Cost-aware Generalized $α$-investing for Multiple Hypothesis Testing

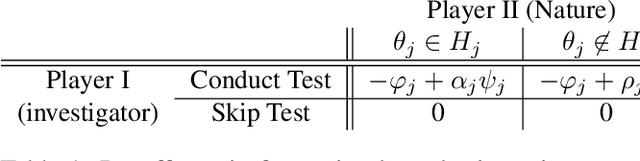
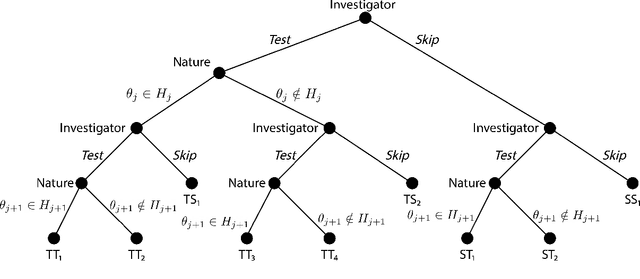
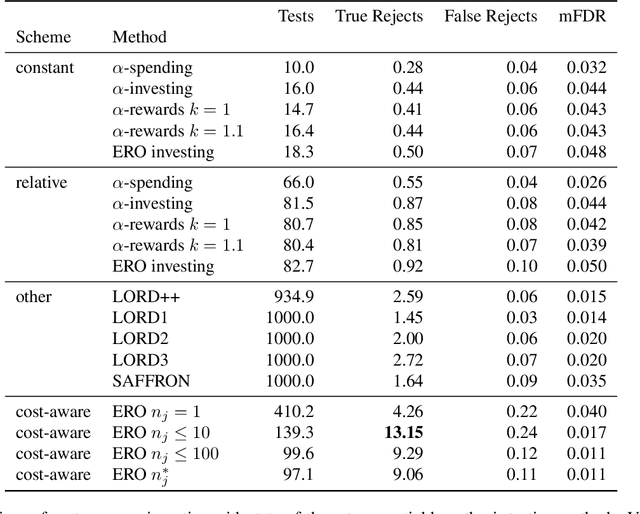
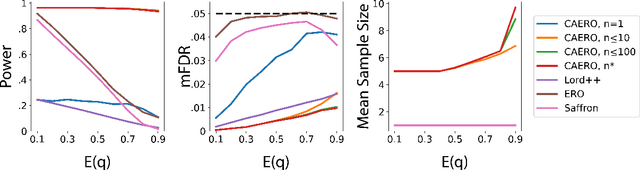
We consider the problem of sequential multiple hypothesis testing with nontrivial data collection cost. This problem appears, for example, when conducting biological experiments to identify differentially expressed genes in a disease process. This work builds on the generalized $\alpha$-investing framework that enables control of the false discovery rate in a sequential testing setting. We make a theoretical analysis of the long term asymptotic behavior of $\alpha$-wealth which motivates a consideration of sample size in the $\alpha$-investing decision rule. Using the game theoretic principle of indifference, we construct a decision rule that optimizes the expected return (ERO) of $\alpha$-wealth and provides an optimal sample size for the test. We show empirical results that a cost-aware ERO decision rule correctly rejects more false null hypotheses than other methods. We extend cost-aware ERO investing to finite-horizon testing which enables the decision rule to hedge against the risk of unproductive tests. Finally, empirical tests on a real data set from a biological experiment show that cost-aware ERO produces actionable decisions as to which tests to conduct and if so at what sample size.