Multimodal Datasets with Controllable Mutual Information

We introduce a framework for generating highly multimodal datasets with explicitly calculable mutual information between modalities. This enables the construction of benchmark datasets that provide a novel testbed for systematic studies of mutual information estimators and multimodal self-supervised learning techniques. Our framework constructs realistic datasets with known mutual information using a flow-based generative model and a structured causal framework for generating correlated latent variables.

Neural Quasiprobabilistic Likelihood Ratio Estimation with Negatively Weighted Data

Motivated by real-world situations found in high energy particle physics, we consider a generalisation of the likelihood-ratio estimation task to a quasiprobabilistic setting where probability densities can be negative. By extension, this framing also applies to importance sampling in a setting where the importance weights can be negative. The presence of negative densities and negative weights, pose an array of challenges to traditional neural likelihood ratio estimation methods. We address these challenges by introducing a novel loss function. In addition, we introduce a new model architecture based on the decomposition of a likelihood ratio using signed mixture models, providing a second strategy for overcoming these challenges. Finally, we demonstrate our approach on a pedagogical example and a real-world example from particle physics.

Transforming the Bootstrap: Using Transformers to Compute Scattering Amplitudes in Planar N = 4 Super Yang-Mills Theory

We pursue the use of deep learning methods to improve state-of-the-art computations in theoretical high-energy physics. Planar N = 4 Super Yang-Mills theory is a close cousin to the theory that describes Higgs boson production at the Large Hadron Collider; its scattering amplitudes are large mathematical expressions containing integer coefficients. In this paper, we apply Transformers to predict these coefficients. The problem can be formulated in a language-like representation amenable to standard cross-entropy training objectives. We design two related experiments and show that the model achieves high accuracy (> 98%) on both tasks. Our work shows that Transformers can be applied successfully to problems in theoretical physics that require exact solutions.

Robust Anomaly Detection for Particle Physics Using Multi-Background Representation Learning

Anomaly, or out-of-distribution, detection is a promising tool for aiding discoveries of new particles or processes in particle physics. In this work, we identify and address two overlooked opportunities to improve anomaly detection for high-energy physics. First, rather than train a generative model on the single most dominant background process, we build detection algorithms using representation learning from multiple background types, thus taking advantage of more information to improve estimation of what is relevant for detection. Second, we generalize decorrelation to the multi-background setting, thus directly enforcing a more complete definition of robustness for anomaly detection. We demonstrate the benefit of the proposed robust multi-background anomaly detection algorithms on a high-dimensional dataset of particle decays at the Large Hadron Collider.

Advances in machine-learning-based sampling motivated by lattice quantum chromodynamics

Sampling from known probability distributions is a ubiquitous task in computational science, underlying calculations in domains from linguistics to biology and physics. Generative machine-learning (ML) models have emerged as a promising tool in this space, building on the success of this approach in applications such as image, text, and audio generation. Often, however, generative tasks in scientific domains have unique structures and features -- such as complex symmetries and the requirement of exactness guarantees -- that present both challenges and opportunities for ML. This Perspective outlines the advances in ML-based sampling motivated by lattice quantum field theory, in particular for the theory of quantum chromodynamics. Enabling calculations of the structure and interactions of matter from our most fundamental understanding of particle physics, lattice quantum chromodynamics is one of the main consumers of open-science supercomputing worldwide. The design of ML algorithms for this application faces profound challenges, including the necessity of scaling custom ML architectures to the largest supercomputers, but also promises immense benefits, and is spurring a wave of development in ML-based sampling more broadly. In lattice field theory, if this approach can realize its early promise it will be a transformative step towards first-principles physics calculations in particle, nuclear and condensed matter physics that are intractable with traditional approaches.

Normalizing flows for lattice gauge theory in arbitrary space-time dimension

Applications of normalizing flows to the sampling of field configurations in lattice gauge theory have so far been explored almost exclusively in two space-time dimensions. We report new algorithmic developments of gauge-equivariant flow architectures facilitating the generalization to higher-dimensional lattice geometries. Specifically, we discuss masked autoregressive transformations with tractable and unbiased Jacobian determinants, a key ingredient for scalable and asymptotically exact flow-based sampling algorithms. For concreteness, results from a proof-of-principle application to SU(3) lattice gauge theory in four space-time dimensions are reported.

Configurable calorimeter simulation for AI applications

A configurable calorimeter simulation for AI (COCOA) applications is presented, based on the Geant4 toolkit and interfaced with the Pythia event generator. This open-source project is aimed to support the development of machine learning algorithms in high energy physics that rely on realistic particle shower descriptions, such as reconstruction, fast simulation, and low-level analysis. Specifications such as the granularity and material of its nearly hermetic geometry are user-configurable. The tool is supplemented with simple event processing including topological clustering, jet algorithms, and a nearest-neighbors graph construction. Formatting is also provided to visualise events using the Phoenix event display software.

AI for Science: An Emerging Agenda

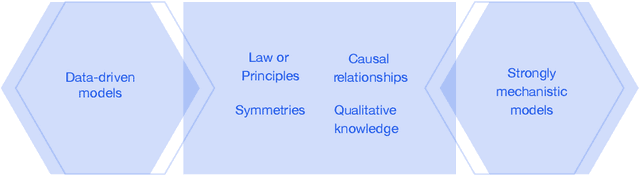
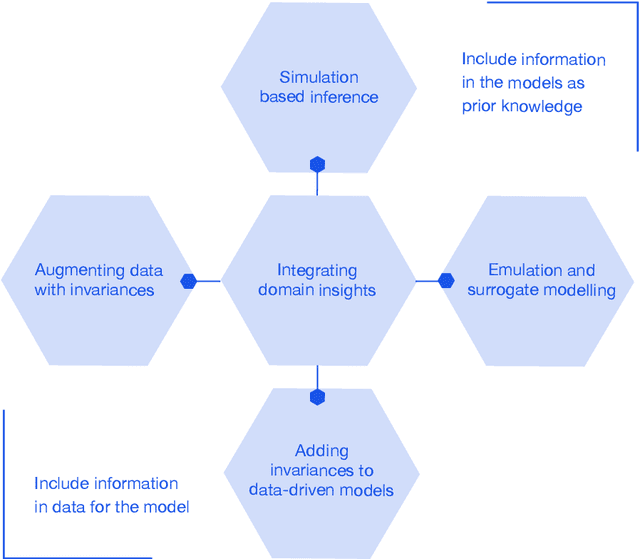
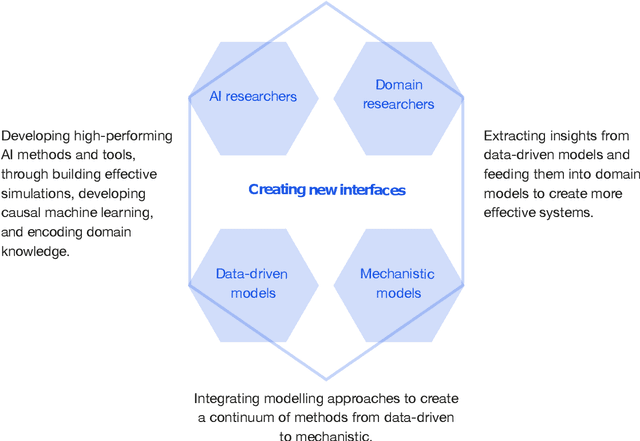
This report documents the programme and the outcomes of Dagstuhl Seminar 22382 "Machine Learning for Science: Bridging Data-Driven and Mechanistic Modelling". Today's scientific challenges are characterised by complexity. Interconnected natural, technological, and human systems are influenced by forces acting across time- and spatial-scales, resulting in complex interactions and emergent behaviours. Understanding these phenomena -- and leveraging scientific advances to deliver innovative solutions to improve society's health, wealth, and well-being -- requires new ways of analysing complex systems. The transformative potential of AI stems from its widespread applicability across disciplines, and will only be achieved through integration across research domains. AI for science is a rendezvous point. It brings together expertise from $\mathrm{AI}$ and application domains; combines modelling knowledge with engineering know-how; and relies on collaboration across disciplines and between humans and machines. Alongside technical advances, the next wave of progress in the field will come from building a community of machine learning researchers, domain experts, citizen scientists, and engineers working together to design and deploy effective AI tools. This report summarises the discussions from the seminar and provides a roadmap to suggest how different communities can collaborate to deliver a new wave of progress in AI and its application for scientific discovery.

Aspects of scaling and scalability for flow-based sampling of lattice QCD

Recent applications of machine-learned normalizing flows to sampling in lattice field theory suggest that such methods may be able to mitigate critical slowing down and topological freezing. However, these demonstrations have been at the scale of toy models, and it remains to be determined whether they can be applied to state-of-the-art lattice quantum chromodynamics calculations. Assessing the viability of sampling algorithms for lattice field theory at scale has traditionally been accomplished using simple cost scaling laws, but as we discuss in this work, their utility is limited for flow-based approaches. We conclude that flow-based approaches to sampling are better thought of as a broad family of algorithms with different scaling properties, and that scalability must be assessed experimentally.

Gauge-equivariant flow models for sampling in lattice field theories with pseudofermions

This work presents gauge-equivariant architectures for flow-based sampling in fermionic lattice field theories using pseudofermions as stochastic estimators for the fermionic determinant. This is the default approach in state-of-the-art lattice field theory calculations, making this development critical to the practical application of flow models to theories such as QCD. Methods by which flow-based sampling approaches can be improved via standard techniques such as even/odd preconditioning and the Hasenbusch factorization are also outlined. Numerical demonstrations in two-dimensional U(1) and SU(3) gauge theories with $N_f=2$ flavors of fermions are provided.