Exploring gauge-fixing conditions with gradient-based optimization

Lattice gauge fixing is required to compute gauge-variant quantities, for example those used in RI-MOM renormalization schemes or as objects of comparison for model calculations. Recently, gauge-variant quantities have also been found to be more amenable to signal-to-noise optimization using contour deformations. These applications motivate systematic parameterization and exploration of gauge-fixing schemes. This work introduces a differentiable parameterization of gauge fixing which is broad enough to cover Landau gauge, Coulomb gauge, and maximal tree gauges. The adjoint state method allows gradient-based optimization to select gauge-fixing schemes that minimize an arbitrary target loss function.

Practical applications of machine-learned flows on gauge fields

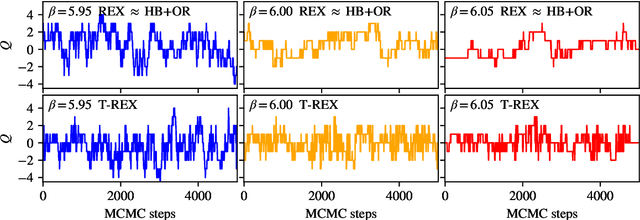
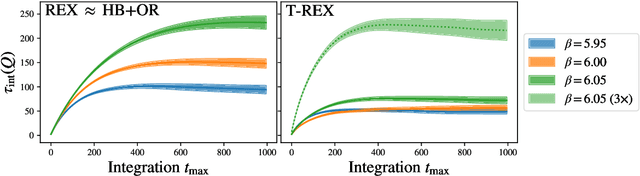
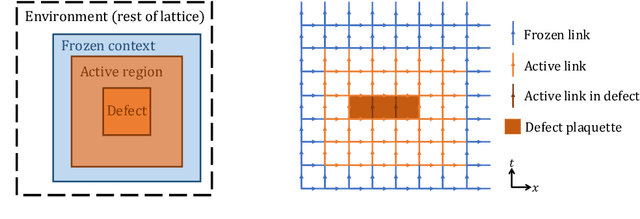
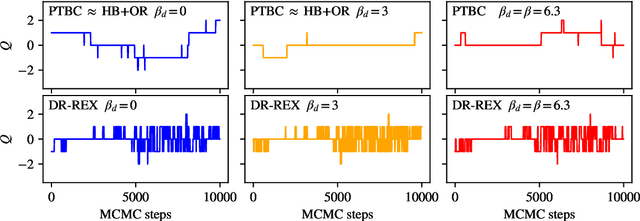
Normalizing flows are machine-learned maps between different lattice theories which can be used as components in exact sampling and inference schemes. Ongoing work yields increasingly expressive flows on gauge fields, but it remains an open question how flows can improve lattice QCD at state-of-the-art scales. We discuss and demonstrate two applications of flows in replica exchange (parallel tempering) sampling, aimed at improving topological mixing, which are viable with iterative improvements upon presently available flows.

Applications of flow models to the generation of correlated lattice QCD ensembles

Machine-learned normalizing flows can be used in the context of lattice quantum field theory to generate statistically correlated ensembles of lattice gauge fields at different action parameters. This work demonstrates how these correlations can be exploited for variance reduction in the computation of observables. Three different proof-of-concept applications are demonstrated using a novel residual flow architecture: continuum limits of gauge theories, the mass dependence of QCD observables, and hadronic matrix elements based on the Feynman-Hellmann approach. In all three cases, it is shown that statistical uncertainties are significantly reduced when machine-learned flows are incorporated as compared with the same calculations performed with uncorrelated ensembles or direct reweighting.

Advances in machine-learning-based sampling motivated by lattice quantum chromodynamics

Sampling from known probability distributions is a ubiquitous task in computational science, underlying calculations in domains from linguistics to biology and physics. Generative machine-learning (ML) models have emerged as a promising tool in this space, building on the success of this approach in applications such as image, text, and audio generation. Often, however, generative tasks in scientific domains have unique structures and features -- such as complex symmetries and the requirement of exactness guarantees -- that present both challenges and opportunities for ML. This Perspective outlines the advances in ML-based sampling motivated by lattice quantum field theory, in particular for the theory of quantum chromodynamics. Enabling calculations of the structure and interactions of matter from our most fundamental understanding of particle physics, lattice quantum chromodynamics is one of the main consumers of open-science supercomputing worldwide. The design of ML algorithms for this application faces profound challenges, including the necessity of scaling custom ML architectures to the largest supercomputers, but also promises immense benefits, and is spurring a wave of development in ML-based sampling more broadly. In lattice field theory, if this approach can realize its early promise it will be a transformative step towards first-principles physics calculations in particle, nuclear and condensed matter physics that are intractable with traditional approaches.

Normalizing flows for lattice gauge theory in arbitrary space-time dimension

Applications of normalizing flows to the sampling of field configurations in lattice gauge theory have so far been explored almost exclusively in two space-time dimensions. We report new algorithmic developments of gauge-equivariant flow architectures facilitating the generalization to higher-dimensional lattice geometries. Specifically, we discuss masked autoregressive transformations with tractable and unbiased Jacobian determinants, a key ingredient for scalable and asymptotically exact flow-based sampling algorithms. For concreteness, results from a proof-of-principle application to SU(3) lattice gauge theory in four space-time dimensions are reported.

Gauge-equivariant flow models for sampling in lattice field theories with pseudofermions

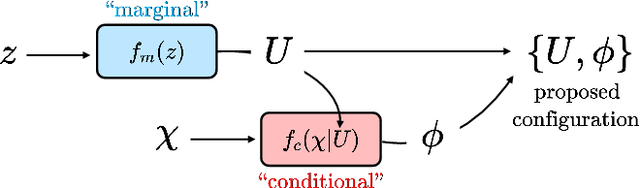
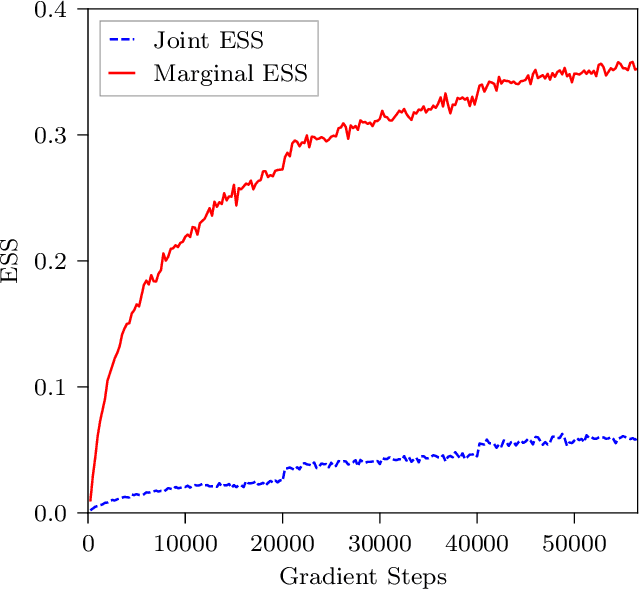
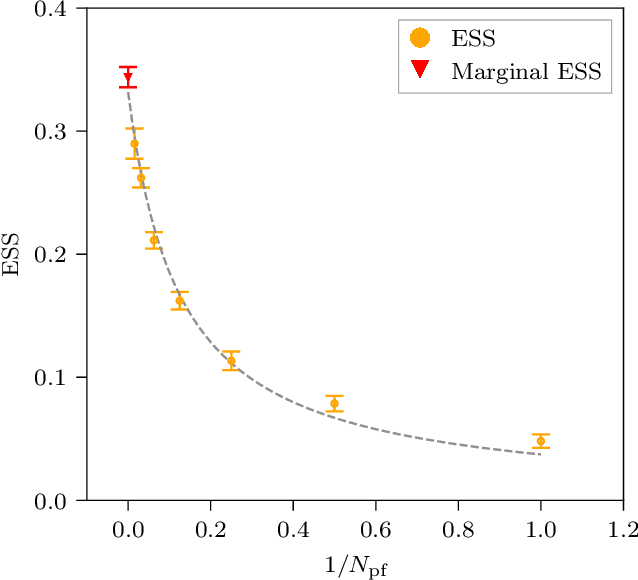
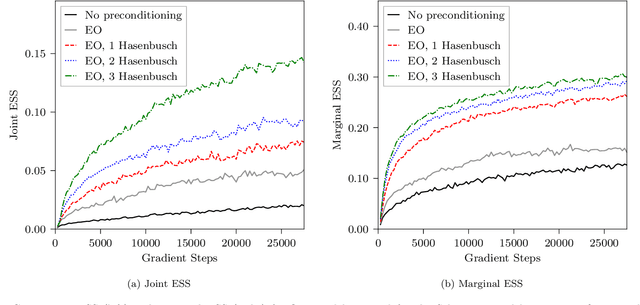
This work presents gauge-equivariant architectures for flow-based sampling in fermionic lattice field theories using pseudofermions as stochastic estimators for the fermionic determinant. This is the default approach in state-of-the-art lattice field theory calculations, making this development critical to the practical application of flow models to theories such as QCD. Methods by which flow-based sampling approaches can be improved via standard techniques such as even/odd preconditioning and the Hasenbusch factorization are also outlined. Numerical demonstrations in two-dimensional U(1) and SU(3) gauge theories with $N_f=2$ flavors of fermions are provided.

Flow-based sampling in the lattice Schwinger model at criticality

Recent results suggest that flow-based algorithms may provide efficient sampling of field distributions for lattice field theory applications, such as studies of quantum chromodynamics and the Schwinger model. In this work, we provide a numerical demonstration of robust flow-based sampling in the Schwinger model at the critical value of the fermion mass. In contrast, at the same parameters, conventional methods fail to sample all parts of configuration space, leading to severely underestimated uncertainties.

Flow-based sampling for multimodal distributions in lattice field theory

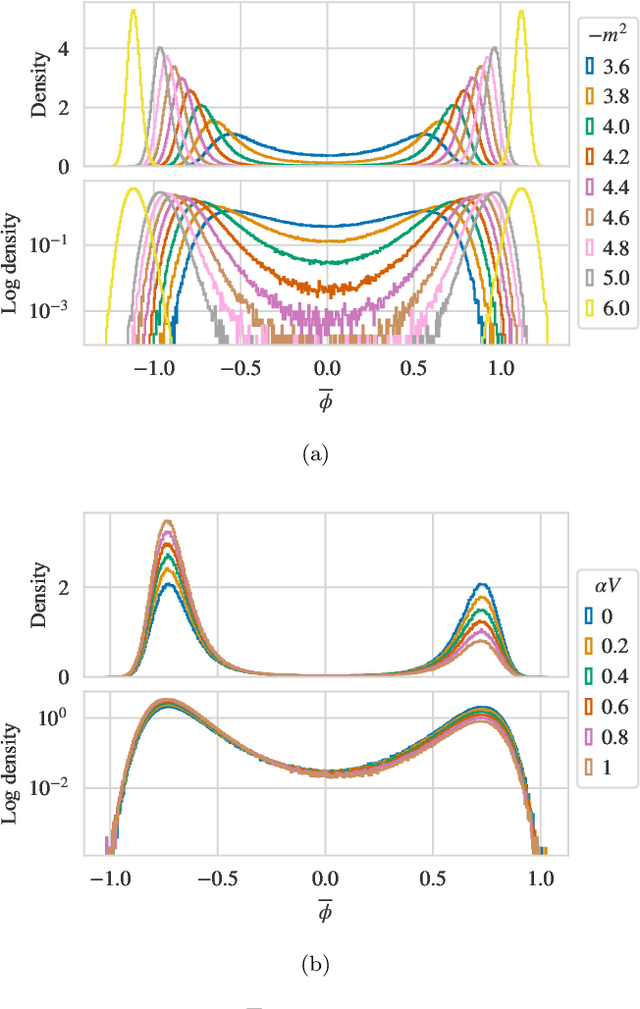
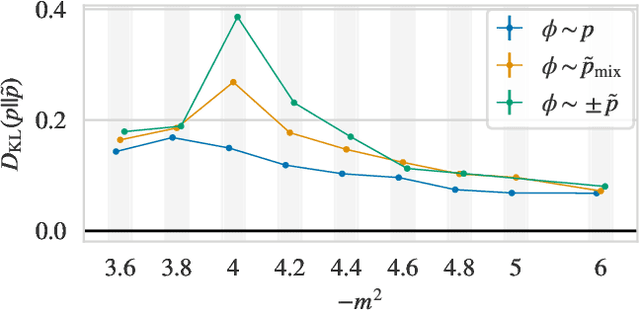
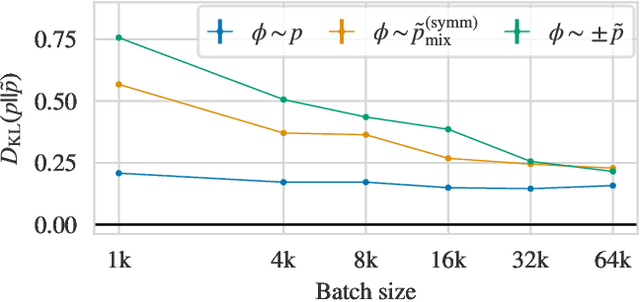
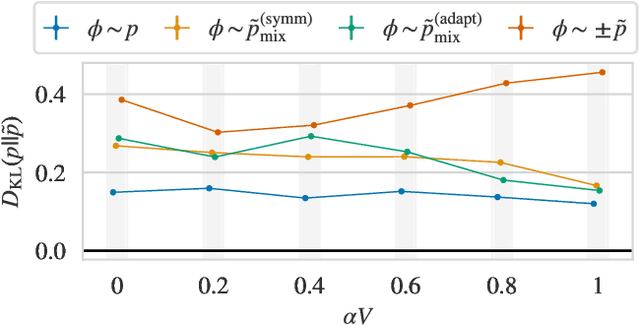
Recent results have demonstrated that samplers constructed with flow-based generative models are a promising new approach for configuration generation in lattice field theory. In this paper, we present a set of methods to construct flow models for targets with multiple separated modes (i.e. theories with multiple vacua). We demonstrate the application of these methods to modeling two-dimensional real scalar field theory in its symmetry-broken phase. In this context we investigate the performance of different flow-based sampling algorithms, including a composite sampling algorithm where flow-based proposals are occasionally augmented by applying updates using traditional algorithms like HMC.

Flow-based sampling for fermionic lattice field theories

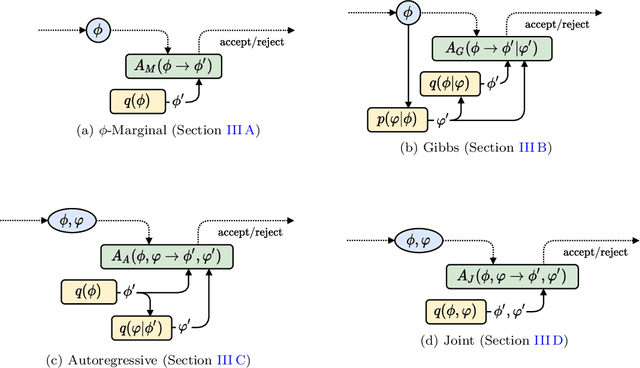
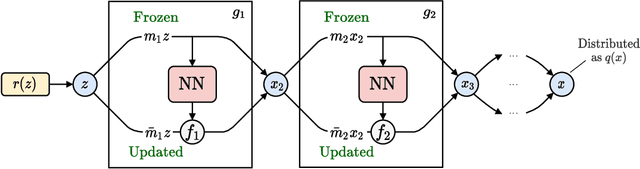
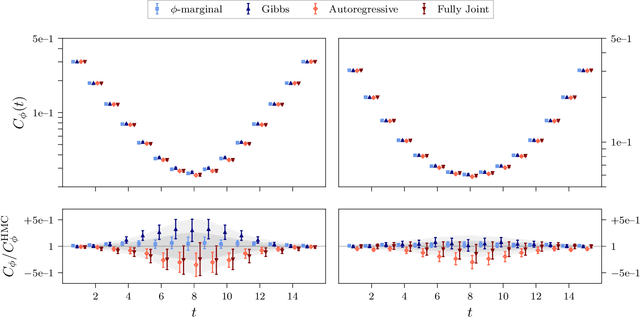
Algorithms based on normalizing flows are emerging as promising machine learning approaches to sampling complicated probability distributions in a way that can be made asymptotically exact. In the context of lattice field theory, proof-of-principle studies have demonstrated the effectiveness of this approach for scalar theories, gauge theories, and statistical systems. This work develops approaches that enable flow-based sampling of theories with dynamical fermions, which is necessary for the technique to be applied to lattice field theory studies of the Standard Model of particle physics and many condensed matter systems. As a practical demonstration, these methods are applied to the sampling of field configurations for a two-dimensional theory of massless staggered fermions coupled to a scalar field via a Yukawa interaction.

Machine Learning and Variational Algorithms for Lattice Field Theory

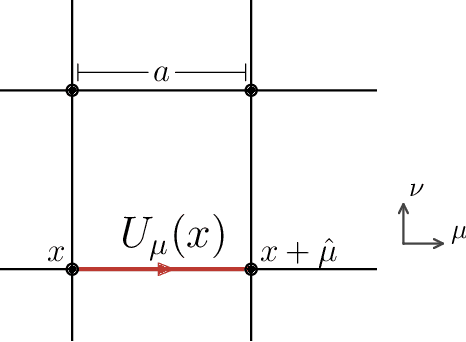
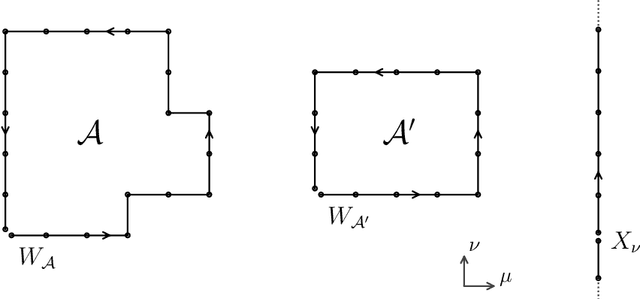
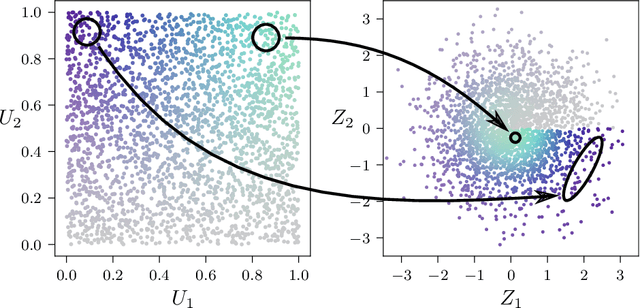
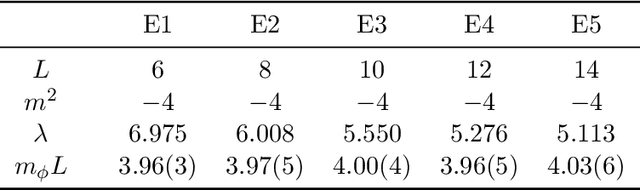
In lattice quantum field theory studies, parameters defining the lattice theory must be tuned toward criticality to access continuum physics. Commonly used Markov chain Monte Carlo (MCMC) methods suffer from critical slowing down in this limit, restricting the precision of continuum extrapolations. Further difficulties arise when measuring correlation functions of operators widely separated in spacetime: for most correlation functions, an exponentially severe signal-to-noise problem is encountered as the operators are taken to be widely separated. This dissertation details two new techniques to address these issues. First, we define a novel MCMC algorithm based on generative flow-based models. Such models utilize machine learning methods to describe efficient approximate samplers for distributions of interest. Independently drawn flow-based samples are then used as proposals in an asymptotically exact Metropolis-Hastings Markov chain. We address incorporating symmetries of interest, including translational and gauge symmetries. We secondly introduce an approach to "deform" Monte Carlo estimators based on contour deformations applied to the domain of the path integral. The deformed estimators associated with an observable give equivalent unbiased measurements of that observable, but generically have different variances. We define families of deformed manifolds for lattice gauge theories and introduce methods to efficiently optimize the choice of manifold (the "observifold"), minimizing the deformed observable variance. Finally, we demonstrate that flow-based MCMC can mitigate critical slowing down and observifolds can exponentially reduce variance in proof-of-principle applications to scalar $\phi^4$ theory and $\mathrm{U}(1)$ and $\mathrm{SU}(N)$ lattice gauge theories.