Jet Discrimination with Quantum Complete Graph Neural Network

Machine learning, particularly deep neural networks, has been widely utilized in high energy physics and has shown remarkable results in various applications. Moreover, the concept of machine learning has been extended to quantum computers, giving rise to a new research area known as quantum machine learning. In this paper, we propose a novel variational quantum circuit model, Quantum Complete Graph Neural Network (QCGNN), designed for learning complete graphs. We argue that QCGNN has a polynomial speedup against its classical counterpart, due to the property of quantum parallelism. In this paper, we study the application of QCGNN through the challenging jet discrimination, where the jets are represented with complete graphs. Subsequently, we conduct a comparative analysis with classical graph neural networks to establish a benchmark.

Flow-based sampling for multimodal distributions in lattice field theory

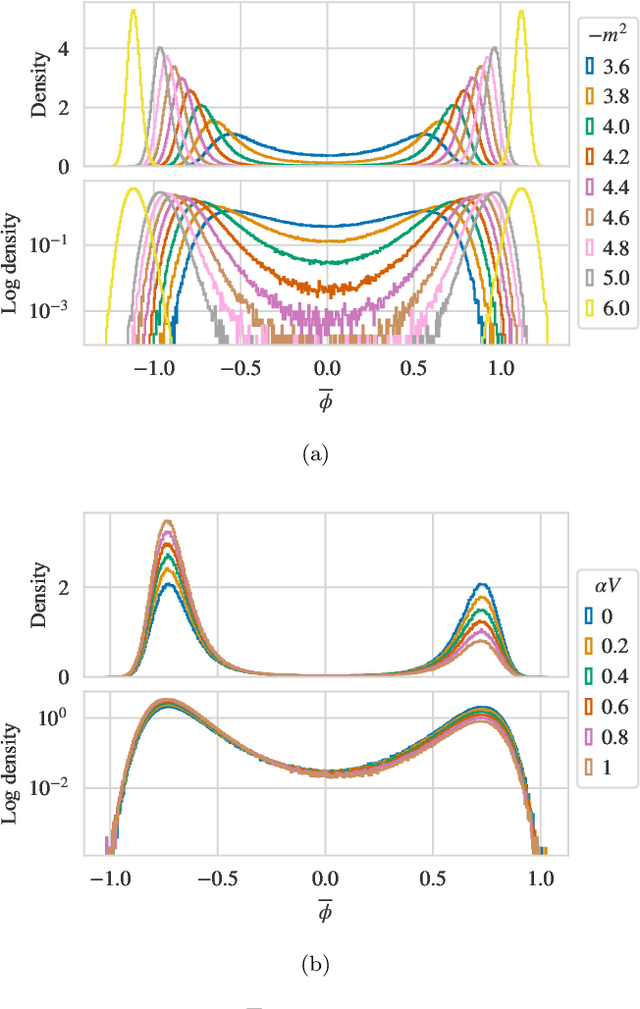
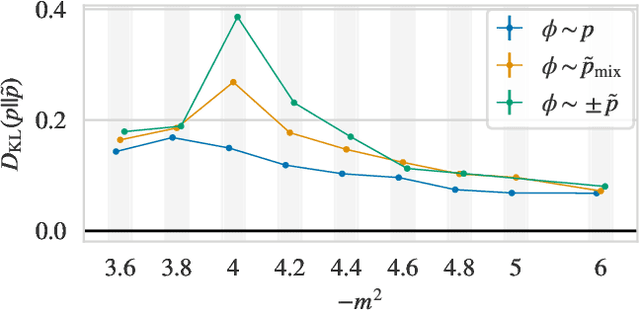
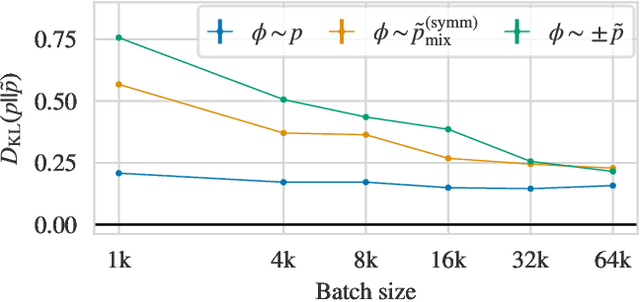
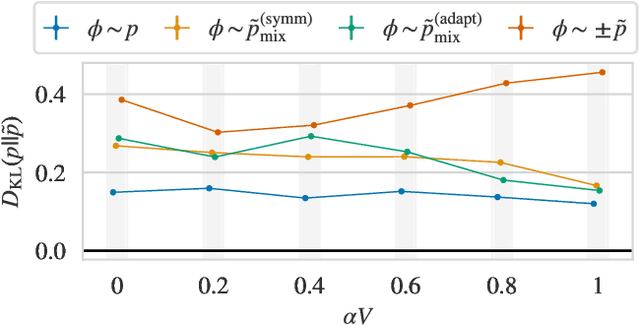
Recent results have demonstrated that samplers constructed with flow-based generative models are a promising new approach for configuration generation in lattice field theory. In this paper, we present a set of methods to construct flow models for targets with multiple separated modes (i.e. theories with multiple vacua). We demonstrate the application of these methods to modeling two-dimensional real scalar field theory in its symmetry-broken phase. In this context we investigate the performance of different flow-based sampling algorithms, including a composite sampling algorithm where flow-based proposals are occasionally augmented by applying updates using traditional algorithms like HMC.