RecurrentGemma: Moving Past Transformers for Efficient Open Language Models

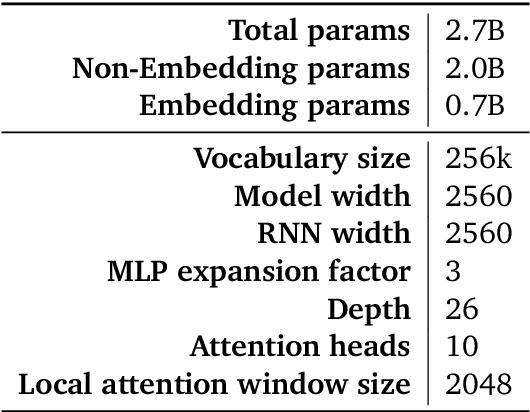
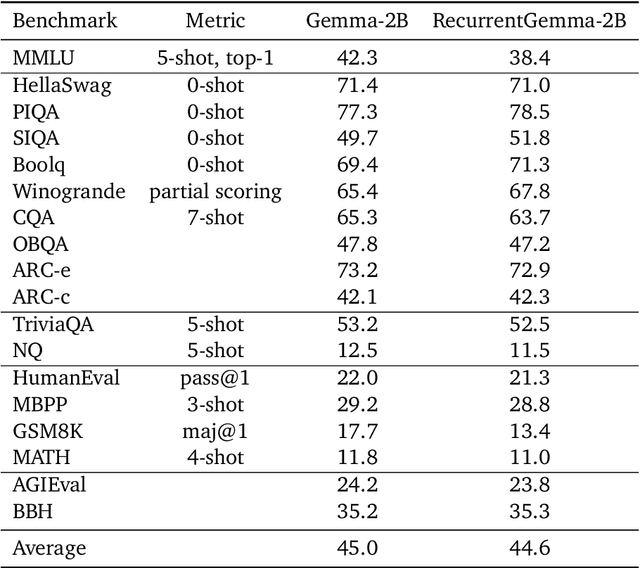
We introduce RecurrentGemma, an open language model which uses Google's novel Griffin architecture. Griffin combines linear recurrences with local attention to achieve excellent performance on language. It has a fixed-sized state, which reduces memory use and enables efficient inference on long sequences. We provide a pre-trained model with 2B non-embedding parameters, and an instruction tuned variant. Both models achieve comparable performance to Gemma-2B despite being trained on fewer tokens.

Griffin: Mixing Gated Linear Recurrences with Local Attention for Efficient Language Models

Recurrent neural networks (RNNs) have fast inference and scale efficiently on long sequences, but they are difficult to train and hard to scale. We propose Hawk, an RNN with gated linear recurrences, and Griffin, a hybrid model that mixes gated linear recurrences with local attention. Hawk exceeds the reported performance of Mamba on downstream tasks, while Griffin matches the performance of Llama-2 despite being trained on over 6 times fewer tokens. We also show that Griffin can extrapolate on sequences significantly longer than those seen during training. Our models match the hardware efficiency of Transformers during training, and during inference they have lower latency and significantly higher throughput. We scale Griffin up to 14B parameters, and explain how to shard our models for efficient distributed training.

Applications of flow models to the generation of correlated lattice QCD ensembles

Machine-learned normalizing flows can be used in the context of lattice quantum field theory to generate statistically correlated ensembles of lattice gauge fields at different action parameters. This work demonstrates how these correlations can be exploited for variance reduction in the computation of observables. Three different proof-of-concept applications are demonstrated using a novel residual flow architecture: continuum limits of gauge theories, the mass dependence of QCD observables, and hadronic matrix elements based on the Feynman-Hellmann approach. In all three cases, it is shown that statistical uncertainties are significantly reduced when machine-learned flows are incorporated as compared with the same calculations performed with uncorrelated ensembles or direct reweighting.

Normalizing flows for lattice gauge theory in arbitrary space-time dimension

Applications of normalizing flows to the sampling of field configurations in lattice gauge theory have so far been explored almost exclusively in two space-time dimensions. We report new algorithmic developments of gauge-equivariant flow architectures facilitating the generalization to higher-dimensional lattice geometries. Specifically, we discuss masked autoregressive transformations with tractable and unbiased Jacobian determinants, a key ingredient for scalable and asymptotically exact flow-based sampling algorithms. For concreteness, results from a proof-of-principle application to SU(3) lattice gauge theory in four space-time dimensions are reported.

Deep Transformers without Shortcuts: Modifying Self-attention for Faithful Signal Propagation

Skip connections and normalisation layers form two standard architectural components that are ubiquitous for the training of Deep Neural Networks (DNNs), but whose precise roles are poorly understood. Recent approaches such as Deep Kernel Shaping have made progress towards reducing our reliance on them, using insights from wide NN kernel theory to improve signal propagation in vanilla DNNs (which we define as networks without skips or normalisation). However, these approaches are incompatible with the self-attention layers present in transformers, whose kernels are intrinsically more complicated to analyse and control. And so the question remains: is it possible to train deep vanilla transformers? We answer this question in the affirmative by designing several approaches that use combinations of parameter initialisations, bias matrices and location-dependent rescaling to achieve faithful signal propagation in vanilla transformers. Our methods address various intricacies specific to signal propagation in transformers, including the interaction with positional encoding and causal masking. In experiments on WikiText-103 and C4, our approaches enable deep transformers without normalisation to train at speeds matching their standard counterparts, and deep vanilla transformers to reach the same performance as standard ones after about 5 times more iterations.

Aspects of scaling and scalability for flow-based sampling of lattice QCD

Recent applications of machine-learned normalizing flows to sampling in lattice field theory suggest that such methods may be able to mitigate critical slowing down and topological freezing. However, these demonstrations have been at the scale of toy models, and it remains to be determined whether they can be applied to state-of-the-art lattice quantum chromodynamics calculations. Assessing the viability of sampling algorithms for lattice field theory at scale has traditionally been accomplished using simple cost scaling laws, but as we discuss in this work, their utility is limited for flow-based approaches. We conclude that flow-based approaches to sampling are better thought of as a broad family of algorithms with different scaling properties, and that scalability must be assessed experimentally.

Deep Learning without Shortcuts: Shaping the Kernel with Tailored Rectifiers

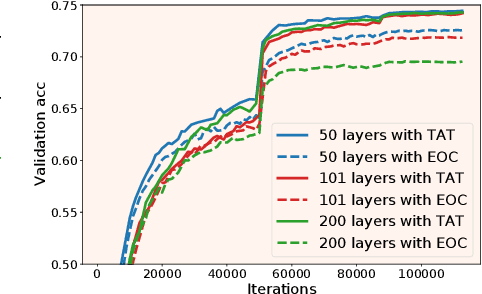
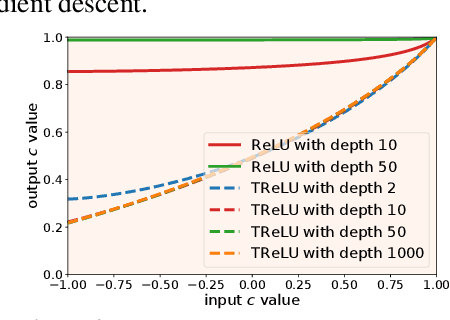
Training very deep neural networks is still an extremely challenging task. The common solution is to use shortcut connections and normalization layers, which are both crucial ingredients in the popular ResNet architecture. However, there is strong evidence to suggest that ResNets behave more like ensembles of shallower networks than truly deep ones. Recently, it was shown that deep vanilla networks (i.e. networks without normalization layers or shortcut connections) can be trained as fast as ResNets by applying certain transformations to their activation functions. However, this method (called Deep Kernel Shaping) isn't fully compatible with ReLUs, and produces networks that overfit significantly more than ResNets on ImageNet. In this work, we rectify this situation by developing a new type of transformation that is fully compatible with a variant of ReLUs -- Leaky ReLUs. We show in experiments that our method, which introduces negligible extra computational cost, achieves validation accuracies with deep vanilla networks that are competitive with ResNets (of the same width/depth), and significantly higher than those obtained with the Edge of Chaos (EOC) method. And unlike with EOC, the validation accuracies we obtain do not get worse with depth.

SyMetric: Measuring the Quality of Learnt Hamiltonian Dynamics Inferred from Vision

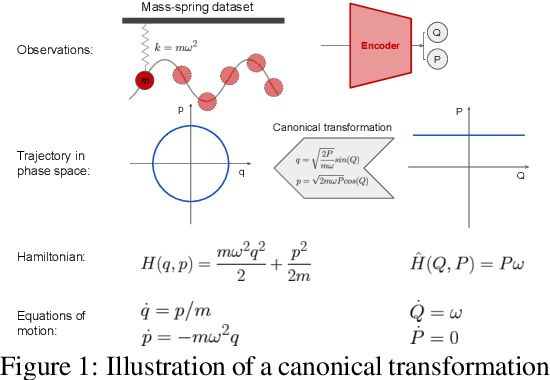
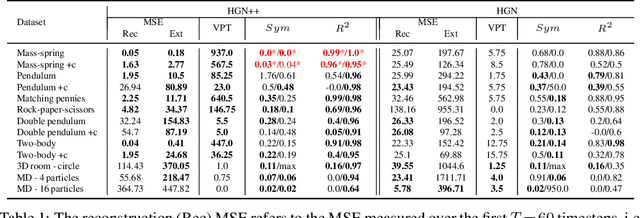
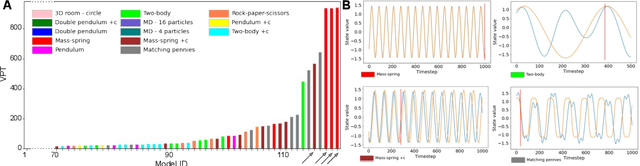
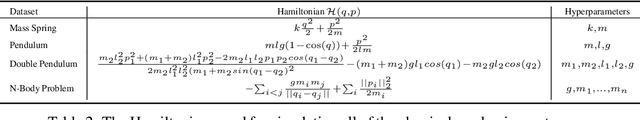
A recently proposed class of models attempts to learn latent dynamics from high-dimensional observations, like images, using priors informed by Hamiltonian mechanics. While these models have important potential applications in areas like robotics or autonomous driving, there is currently no good way to evaluate their performance: existing methods primarily rely on image reconstruction quality, which does not always reflect the quality of the learnt latent dynamics. In this work, we empirically highlight the problems with the existing measures and develop a set of new measures, including a binary indicator of whether the underlying Hamiltonian dynamics have been faithfully captured, which we call Symplecticity Metric or SyMetric. Our measures take advantage of the known properties of Hamiltonian dynamics and are more discriminative of the model's ability to capture the underlying dynamics than reconstruction error. Using SyMetric, we identify a set of architectural choices that significantly improve the performance of a previously proposed model for inferring latent dynamics from pixels, the Hamiltonian Generative Network (HGN). Unlike the original HGN, the new HGN++ is able to discover an interpretable phase space with physically meaningful latents on some datasets. Furthermore, it is stable for significantly longer rollouts on a diverse range of 13 datasets, producing rollouts of essentially infinite length both forward and backwards in time with no degradation in quality on a subset of the datasets.

Which priors matter? Benchmarking models for learning latent dynamics

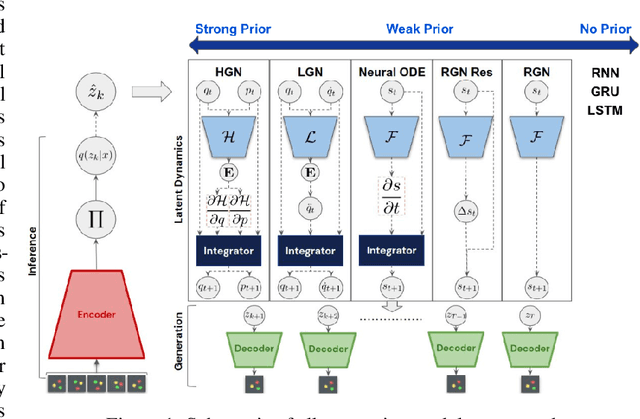
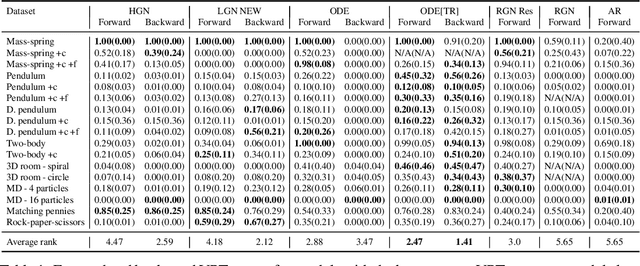
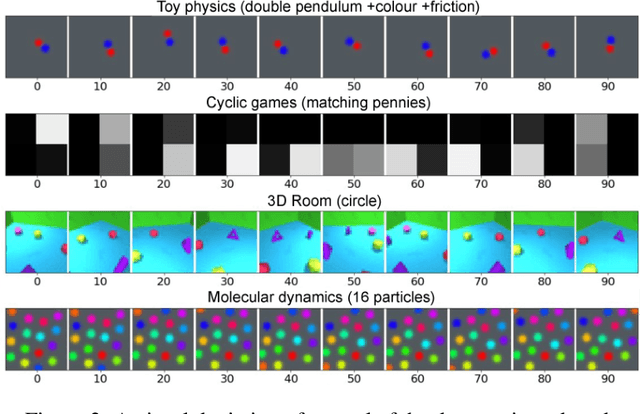
Learning dynamics is at the heart of many important applications of machine learning (ML), such as robotics and autonomous driving. In these settings, ML algorithms typically need to reason about a physical system using high dimensional observations, such as images, without access to the underlying state. Recently, several methods have proposed to integrate priors from classical mechanics into ML models to address the challenge of physical reasoning from images. In this work, we take a sober look at the current capabilities of these models. To this end, we introduce a suite consisting of 17 datasets with visual observations based on physical systems exhibiting a wide range of dynamics. We conduct a thorough and detailed comparison of the major classes of physically inspired methods alongside several strong baselines. While models that incorporate physical priors can often learn latent spaces with desirable properties, our results demonstrate that these methods fail to significantly improve upon standard techniques. Nonetheless, we find that the use of continuous and time-reversible dynamics benefits models of all classes.

Better, Faster Fermionic Neural Networks

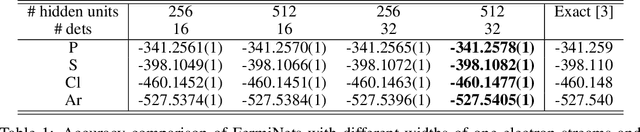
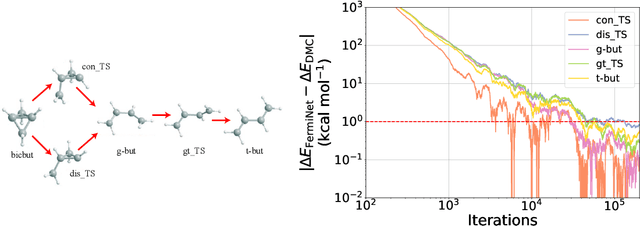
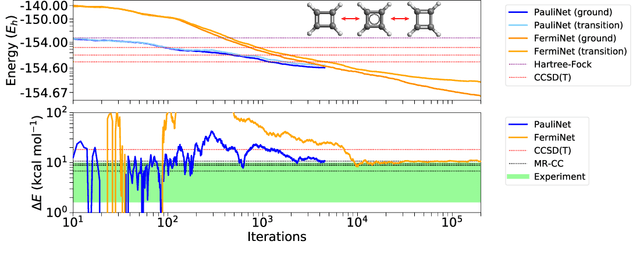
The Fermionic Neural Network (FermiNet) is a recently-developed neural network architecture that can be used as a wavefunction Ansatz for many-electron systems, and has already demonstrated high accuracy on small systems. Here we present several improvements to the FermiNet that allow us to set new records for speed and accuracy on challenging systems. We find that increasing the size of the network is sufficient to reach chemical accuracy on atoms as large as argon. Through a combination of implementing FermiNet in JAX and simplifying several parts of the network, we are able to reduce the number of GPU hours needed to train the FermiNet on large systems by an order of magnitude. This enables us to run the FermiNet on the challenging transition of bicyclobutane to butadiene and compare against the PauliNet on the automerization of cyclobutadiene, and we achieve results near the state of the art for both.