Normalizing flows for lattice gauge theory in arbitrary space-time dimension

Applications of normalizing flows to the sampling of field configurations in lattice gauge theory have so far been explored almost exclusively in two space-time dimensions. We report new algorithmic developments of gauge-equivariant flow architectures facilitating the generalization to higher-dimensional lattice geometries. Specifically, we discuss masked autoregressive transformations with tractable and unbiased Jacobian determinants, a key ingredient for scalable and asymptotically exact flow-based sampling algorithms. For concreteness, results from a proof-of-principle application to SU(3) lattice gauge theory in four space-time dimensions are reported.

Aspects of scaling and scalability for flow-based sampling of lattice QCD

Recent applications of machine-learned normalizing flows to sampling in lattice field theory suggest that such methods may be able to mitigate critical slowing down and topological freezing. However, these demonstrations have been at the scale of toy models, and it remains to be determined whether they can be applied to state-of-the-art lattice quantum chromodynamics calculations. Assessing the viability of sampling algorithms for lattice field theory at scale has traditionally been accomplished using simple cost scaling laws, but as we discuss in this work, their utility is limited for flow-based approaches. We conclude that flow-based approaches to sampling are better thought of as a broad family of algorithms with different scaling properties, and that scalability must be assessed experimentally.

Score-Based Diffusion meets Annealed Importance Sampling

More than twenty years after its introduction, Annealed Importance Sampling (AIS) remains one of the most effective methods for marginal likelihood estimation. It relies on a sequence of distributions interpolating between a tractable initial distribution and the target distribution of interest which we simulate from approximately using a non-homogeneous Markov chain. To obtain an importance sampling estimate of the marginal likelihood, AIS introduces an extended target distribution to reweight the Markov chain proposal. While much effort has been devoted to improving the proposal distribution used by AIS, by changing the intermediate distributions and corresponding Markov kernels, an underappreciated issue is that AIS uses a convenient but suboptimal extended target distribution. This can hinder its performance. We here leverage recent progress in score-based generative modeling (SGM) to approximate the optimal extended target distribution for AIS proposals corresponding to the discretization of Langevin and Hamiltonian dynamics. We demonstrate these novel, differentiable, AIS procedures on a number of synthetic benchmark distributions and variational auto-encoders.

Continual Repeated Annealed Flow Transport Monte Carlo

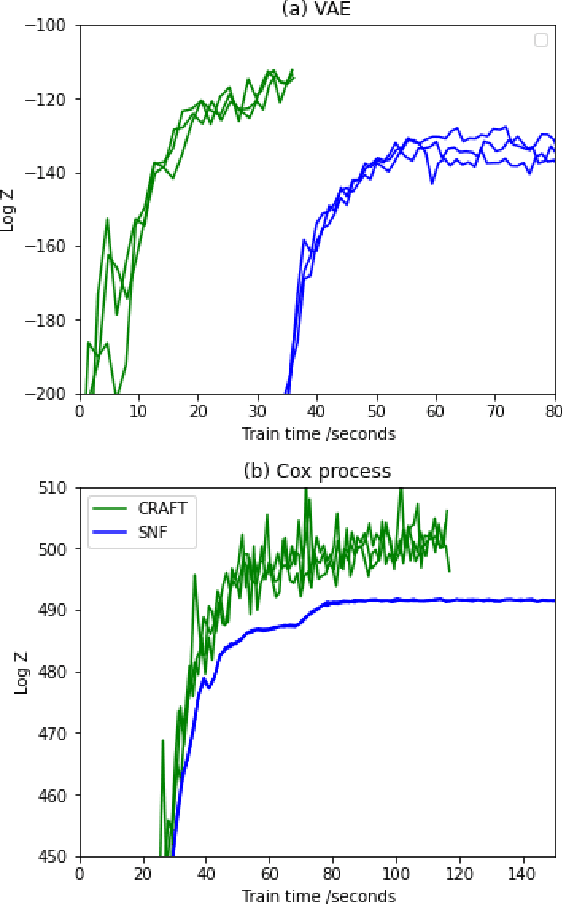
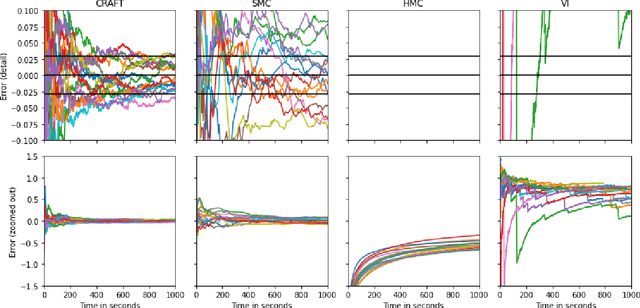
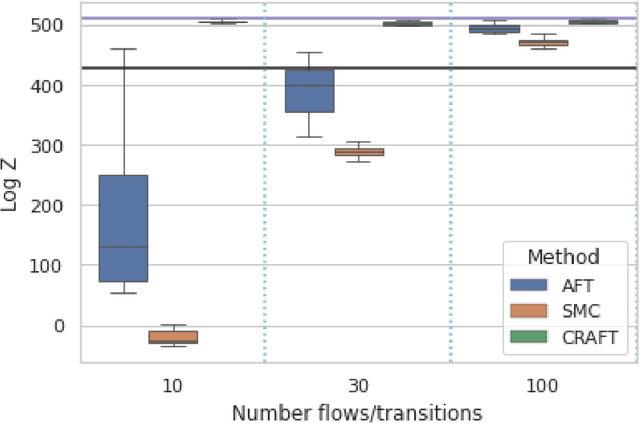
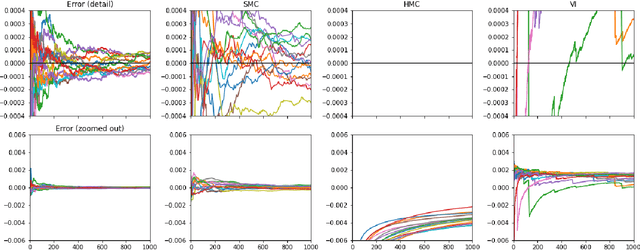
We propose Continual Repeated Annealed Flow Transport Monte Carlo (CRAFT), a method that combines a sequential Monte Carlo (SMC) sampler (itself a generalization of Annealed Importance Sampling) with variational inference using normalizing flows. The normalizing flows are directly trained to transport between annealing temperatures using a KL divergence for each transition. This optimization objective is itself estimated using the normalizing flow/SMC approximation. We show conceptually and using multiple empirical examples that CRAFT improves on Annealed Flow Transport Monte Carlo (Arbel et al., 2021), on which it builds and also on Markov chain Monte Carlo (MCMC) based Stochastic Normalizing Flows (Wu et al., 2020). By incorporating CRAFT within particle MCMC, we show that such learnt samplers can achieve impressively accurate results on a challenging lattice field theory example.

Annealed Flow Transport Monte Carlo

Annealed Importance Sampling (AIS) and its Sequential Monte Carlo (SMC) extensions are state-of-the-art methods for estimating normalizing constants of probability distributions. We propose here a novel Monte Carlo algorithm, Annealed Flow Transport (AFT), that builds upon AIS and SMC and combines them with normalizing flows (NF) for improved performance. This method transports a set of particles using not only importance sampling (IS), Markov chain Monte Carlo (MCMC) and resampling steps - as in SMC, but also relies on NF which are learned sequentially to push particles towards the successive annealed targets. We provide limit theorems for the resulting Monte Carlo estimates of the normalizing constant and expectations with respect to the target distribution. Additionally, we show that a continuous-time scaling limit of the population version of AFT is given by a Feynman--Kac measure which simplifies to the law of a controlled diffusion for expressive NF. We demonstrate experimentally the benefits and limitations of our methodology on a variety of applications.