Laser: Latent Set Representations for 3D Generative Modeling

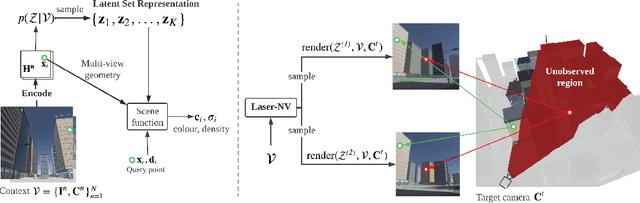
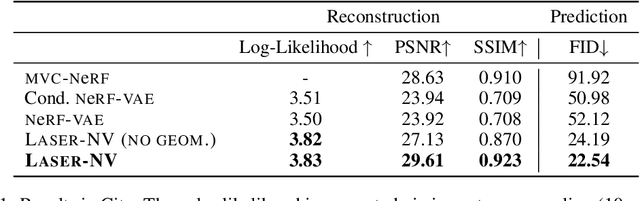
NeRF provides unparalleled fidelity of novel view synthesis: rendering a 3D scene from an arbitrary viewpoint. NeRF requires training on a large number of views that fully cover a scene, which limits its applicability. While these issues can be addressed by learning a prior over scenes in various forms, previous approaches have been either applied to overly simple scenes or struggling to render unobserved parts. We introduce Laser-NV: a generative model which achieves high modelling capacity, and which is based on a set-valued latent representation modelled by normalizing flows. Similarly to previous amortized approaches, Laser-NV learns structure from multiple scenes and is capable of fast, feed-forward inference from few views. To encourage higher rendering fidelity and consistency with observed views, Laser-NV further incorporates a geometry-informed attention mechanism over the observed views. Laser-NV further produces diverse and plausible completions of occluded parts of a scene while remaining consistent with observations. Laser-NV shows state-of-the-art novel-view synthesis quality when evaluated on ShapeNet and on a novel simulated City dataset, which features high uncertainty in the unobserved regions of the scene.

Score-Based Diffusion meets Annealed Importance Sampling

More than twenty years after its introduction, Annealed Importance Sampling (AIS) remains one of the most effective methods for marginal likelihood estimation. It relies on a sequence of distributions interpolating between a tractable initial distribution and the target distribution of interest which we simulate from approximately using a non-homogeneous Markov chain. To obtain an importance sampling estimate of the marginal likelihood, AIS introduces an extended target distribution to reweight the Markov chain proposal. While much effort has been devoted to improving the proposal distribution used by AIS, by changing the intermediate distributions and corresponding Markov kernels, an underappreciated issue is that AIS uses a convenient but suboptimal extended target distribution. This can hinder its performance. We here leverage recent progress in score-based generative modeling (SGM) to approximate the optimal extended target distribution for AIS proposals corresponding to the discretization of Langevin and Hamiltonian dynamics. We demonstrate these novel, differentiable, AIS procedures on a number of synthetic benchmark distributions and variational auto-encoders.

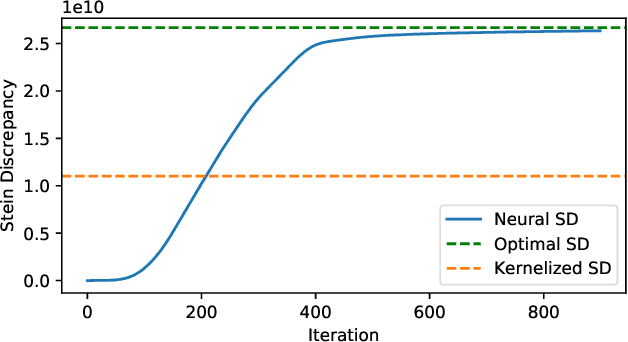
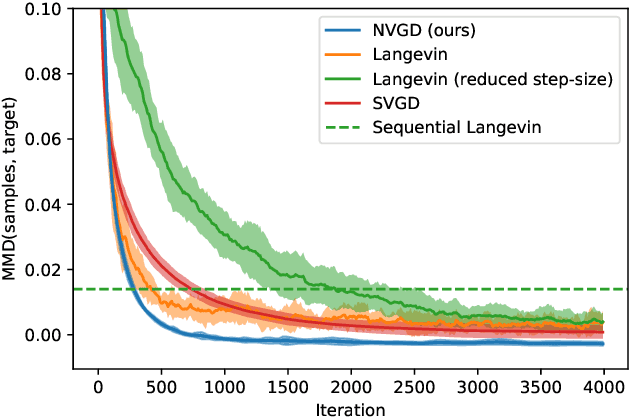
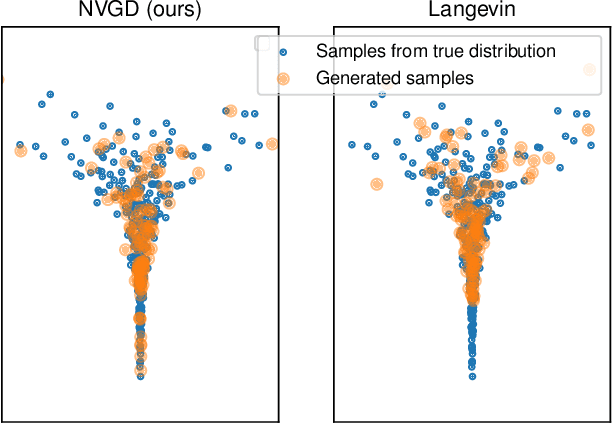
Neural Variational Gradient Descent

Particle-based approximate Bayesian inference approaches such as Stein Variational Gradient Descent (SVGD) combine the flexibility and convergence guarantees of sampling methods with the computational benefits of variational inference. In practice, SVGD relies on the choice of an appropriate kernel function, which impacts its ability to model the target distribution -- a challenging problem with only heuristic solutions. We propose Neural Variational Gradient Descent (NVGD), which is based on parameterizing the witness function of the Stein discrepancy by a deep neural network whose parameters are learned in parallel to the inference, mitigating the necessity to make any kernel choices whatsoever. We empirically evaluate our method on popular synthetic inference problems, real-world Bayesian linear regression, and Bayesian neural network inference.

NeRF-VAE: A Geometry Aware 3D Scene Generative Model

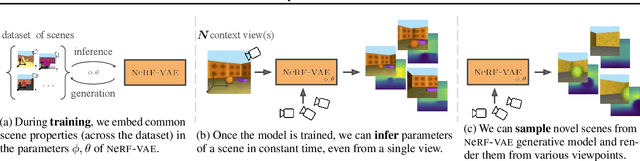
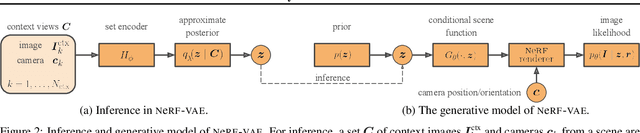
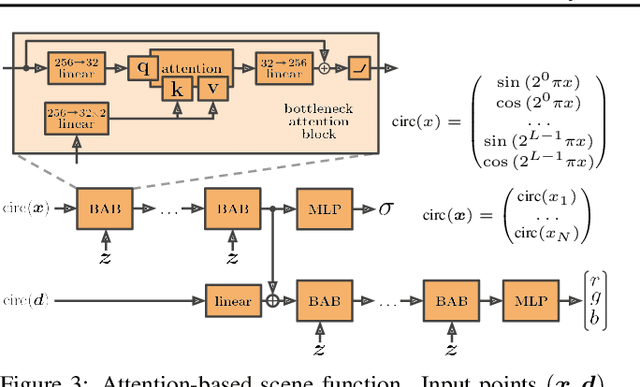
We propose NeRF-VAE, a 3D scene generative model that incorporates geometric structure via NeRF and differentiable volume rendering. In contrast to NeRF, our model takes into account shared structure across scenes, and is able to infer the structure of a novel scene -- without the need to re-train -- using amortized inference. NeRF-VAE's explicit 3D rendering process further contrasts previous generative models with convolution-based rendering which lacks geometric structure. Our model is a VAE that learns a distribution over radiance fields by conditioning them on a latent scene representation. We show that, once trained, NeRF-VAE is able to infer and render geometrically-consistent scenes from previously unseen 3D environments using very few input images. We further demonstrate that NeRF-VAE generalizes well to out-of-distribution cameras, while convolutional models do not. Finally, we introduce and study an attention-based conditioning mechanism of NeRF-VAE's decoder, which improves model performance.

Persistent Message Passing

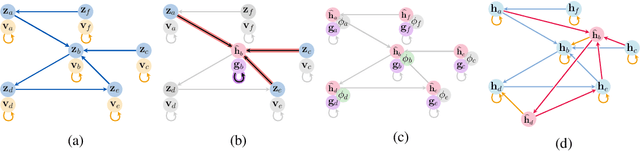
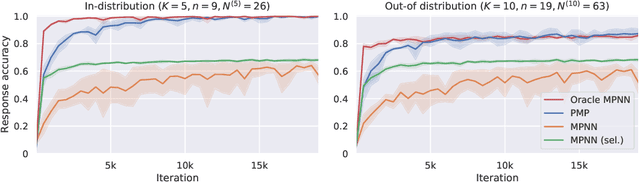
Graph neural networks (GNNs) are a powerful inductive bias for modelling algorithmic reasoning procedures and data structures. Their prowess was mainly demonstrated on tasks featuring Markovian dynamics, where querying any associated data structure depends only on its latest state. For many tasks of interest, however, it may be highly beneficial to support efficient data structure queries dependent on previous states. This requires tracking the data structure's evolution through time, placing significant pressure on the GNN's latent representations. We introduce Persistent Message Passing (PMP), a mechanism which endows GNNs with capability of querying past state by explicitly persisting it: rather than overwriting node representations, it creates new nodes whenever required. PMP generalises out-of-distribution to more than 2x larger test inputs on dynamic temporal range queries, significantly outperforming GNNs which overwrite states.

Learning deep kernels for exponential family densities

The kernel exponential family is a rich class of distributions,which can be fit efficiently and with statistical guarantees by score matching. Being required to choose a priori a simple kernel such as the Gaussian, however, limits its practical applicability. We provide a scheme for learning a kernel parameterized by a deep network, which can find complex location-dependent local features of the data geometry. This gives a very rich class of density models, capable of fitting complex structures on moderate-dimensional problems. Compared to deep density models fit via maximum likelihood, our approach provides a complementary set of strengths and tradeoffs: in empirical studies, the former can yield higher likelihoods, whereas the latter gives better estimates of the gradient of the log density, the score, which describes the distribution's shape.

Scalable Gaussian Processes on Discrete Domains

Kernel methods on discrete domains have shown great promise for many challenging tasks, e.g., on biological sequence data as well as on molecular structures. Scalable kernel methods like support vector machines offer good predictive performances but they often do not provide uncertainty estimates. In contrast, probabilistic kernel methods like Gaussian Processes offer uncertainty estimates in addition to good predictive performance but fall short in terms of scalability. We present the first sparse Gaussian Process approximation framework on discrete input domains. Our framework achieves good predictive performance as well as uncertainty estimates using different discrete optimization techniques. We present competitive results comparing our framework to support vector machine and full Gaussian Process baselines on synthetic data as well as on challenging real-world DNA sequence data.

Deep Self-Organization: Interpretable Discrete Representation Learning on Time Series

High-dimensional time series are common in many domains. Since human cognition is not optimized to work well in high-dimensional spaces, these areas could benefit from interpretable low-dimensional representations. However, most representation learning algorithms for time series data are difficult to interpret. This is due to non-intuitive mappings from data features to salient properties of the representation and non-smoothness over time. To address this problem, we propose a new representation learning framework building on ideas from interpretable discrete dimensionality reduction and deep generative modeling. This framework allows us to learn discrete representations of time series, which give rise to smooth and interpretable embeddings with superior clustering performance. We introduce a new way to overcome the non-differentiability in discrete representation learning and present a gradient-based version of the traditional self-organizing map algorithm that is more performant than the original. Furthermore, to allow for a probabilistic interpretation of our method, we integrate a Markov model in the representation space. This model uncovers the temporal transition structure, improves clustering performance even further and provides additional explanatory insights as well as a natural representation of uncertainty. We evaluate our model in terms of clustering performance and interpretability on static (Fashion-)MNIST data, a time series of linearly interpolated (Fashion-)MNIST images, a chaotic Lorenz attractor system with two macro states, as well as on a challenging real world medical time series application on the eICU data set. Our learned representations compare favorably with competitor methods and facilitate downstream tasks on the real world data.

Efficient and principled score estimation with Nyström kernel exponential families

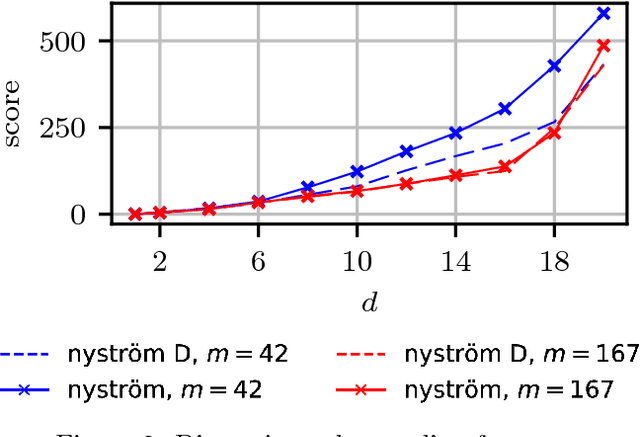
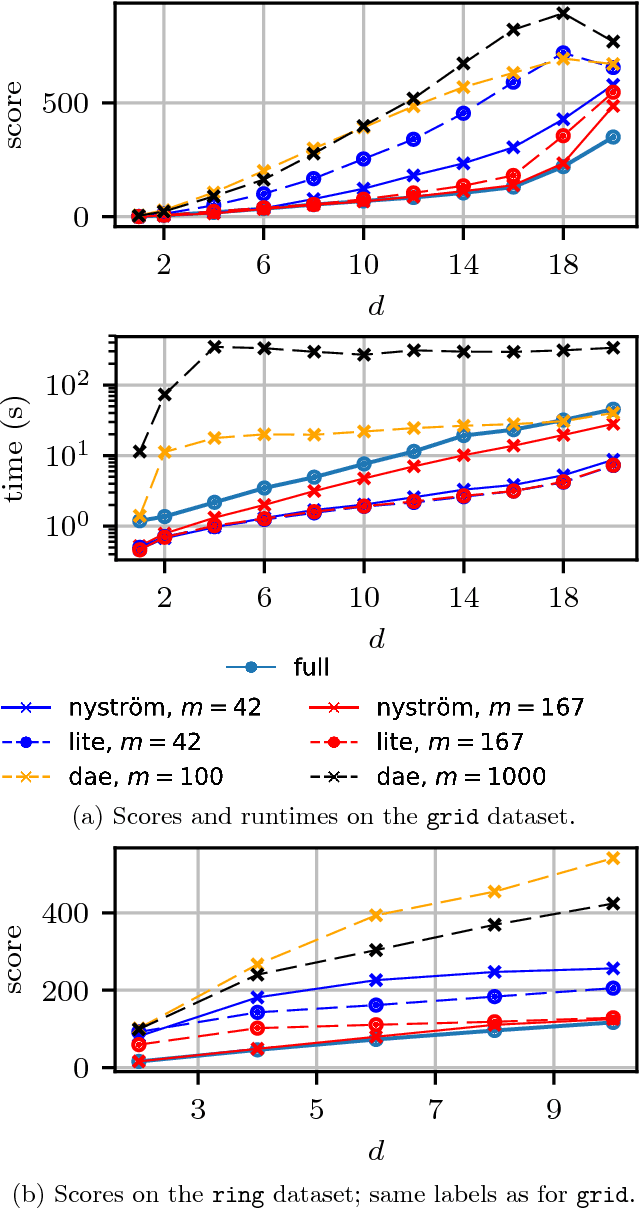
We propose a fast method with statistical guarantees for learning an exponential family density model where the natural parameter is in a reproducing kernel Hilbert space, and may be infinite-dimensional. The model is learned by fitting the derivative of the log density, the score, thus avoiding the need to compute a normalization constant. Our approach improves the computational efficiency of an earlier solution by using a low-rank, Nystr\"om-like solution. The new solution retains the consistency and convergence rates of the full-rank solution (exactly in Fisher distance, and nearly in other distances), with guarantees on the degree of cost and storage reduction. We evaluate the method in experiments on density estimation and in the construction of an adaptive Hamiltonian Monte Carlo sampler. Compared to an existing score learning approach using a denoising autoencoder, our estimator is empirically more data-efficient when estimating the score, runs faster, and has fewer parameters (which can be tuned in a principled and interpretable way), in addition to providing statistical guarantees.

Kernel Sequential Monte Carlo

We propose kernel sequential Monte Carlo (KSMC), a framework for sampling from static target densities. KSMC is a family of sequential Monte Carlo algorithms that are based on building emulator models of the current particle system in a reproducing kernel Hilbert space. We here focus on modelling nonlinear covariance structure and gradients of the target. The emulator's geometry is adaptively updated and subsequently used to inform local proposals. Unlike in adaptive Markov chain Monte Carlo, continuous adaptation does not compromise convergence of the sampler. KSMC combines the strengths of sequental Monte Carlo and kernel methods: superior performance for multimodal targets and the ability to estimate model evidence as compared to Markov chain Monte Carlo, and the emulator's ability to represent targets that exhibit high degrees of nonlinearity. As KSMC does not require access to target gradients, it is particularly applicable on targets whose gradients are unknown or prohibitively expensive. We describe necessary tuning details and demonstrate the benefits of the the proposed methodology on a series of challenging synthetic and real-world examples.