Autoregressive Denoising Diffusion Models for Multivariate Probabilistic Time Series Forecasting

In this work, we propose \texttt{TimeGrad}, an autoregressive model for multivariate probabilistic time series forecasting which samples from the data distribution at each time step by estimating its gradient. To this end, we use diffusion probabilistic models, a class of latent variable models closely connected to score matching and energy-based methods. Our model learns gradients by optimizing a variational bound on the data likelihood and at inference time converts white noise into a sample of the distribution of interest through a Markov chain using Langevin sampling. We demonstrate experimentally that the proposed autoregressive denoising diffusion model is the new state-of-the-art multivariate probabilistic forecasting method on real-world data sets with thousands of correlated dimensions. We hope that this method is a useful tool for practitioners and lays the foundation for future research in this area.

Feature space approximation for kernel-based supervised learning

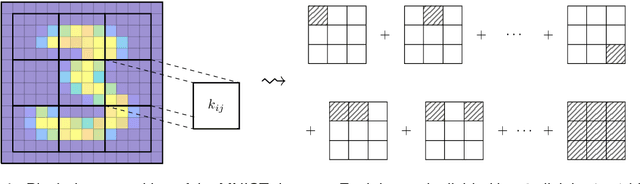
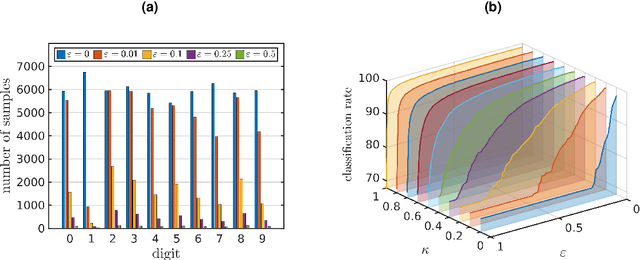
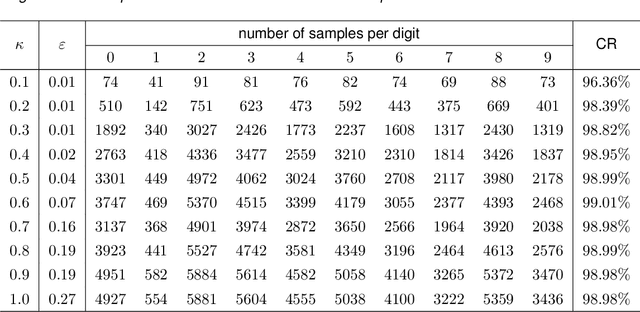
We propose a method for the approximation of high- or even infinite-dimensional feature vectors, which play an important role in supervised learning. The goal is to reduce the size of the training data, resulting in lower storage consumption and computational complexity. Furthermore, the method can be regarded as a regularization technique, which improves the generalizability of learned target functions. We demonstrate significant improvements in comparison to the computation of data-driven predictions involving the full training data set. The method is applied to classification and regression problems from different application areas such as image recognition, system identification, and oceanographic time series analysis.

Multi-variate Probabilistic Time Series Forecasting via Conditioned Normalizing Flows

Time series forecasting is often fundamental to scientific and engineering problems and enables decision making. With ever increasing data set sizes, a trivial solution to scale up predictions is to assume independence between interacting time series. However, modeling statistical dependencies can improve accuracy and enable analysis of interaction effects. Deep learning methods are well suited for this problem, but multi-variate models often assume a simple parametric distribution and do not scale to high dimensions. In this work we model the multi-variate temporal dynamics of time series via an autoregressive deep learning model, where the data distribution is represented by a conditioned normalizing flow. This combination retains the power of autoregressive models, such as good performance in extrapolation into the future, with the flexibility of flows as a general purpose high-dimensional distribution model, while remaining computationally tractable. We show that it improves over the state-of-the-art for standard metrics on many real-world data sets with several thousand interacting time-series.

A Rigorous Theory of Conditional Mean Embeddings

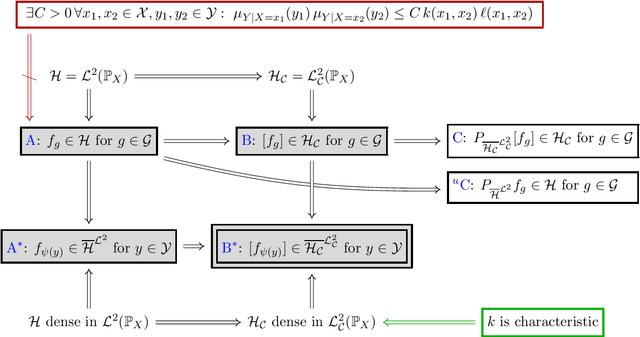
Conditional mean embeddings (CME) have proven themselves to be a powerful tool in many machine learning applications. They allow the efficient conditioning of probability distributions within the corresponding reproducing kernel Hilbert spaces (RKHSs) by providing a linear-algebraic relation for the kernel mean embeddings of the respective probability distributions. Both centered and uncentered covariance operators have been used to define CMEs in the existing literature. In this paper, we develop a mathematically rigorous theory for both variants, discuss the merits and problems of either, and significantly weaken the conditions for applicability of CMEs. In the course of this, we demonstrate a beautiful connection to Gaussian conditioning in Hilbert spaces.

Set Flow: A Permutation Invariant Normalizing Flow

We present a generative model that is defined on finite sets of exchangeable, potentially high dimensional, data. As the architecture is an extension of RealNVPs, it inherits all its favorable properties, such as being invertible and allowing for exact log-likelihood evaluation. We show that this architecture is able to learn finite non-i.i.d. set data distributions, learn statistical dependencies between entities of the set and is able to train and sample with variable set sizes in a computationally efficient manner. Experiments on 3D point clouds show state-of-the art likelihoods.

Kernel Conditional Density Operators

We introduce a conditional density estimation model termed the conditional density operator. It naturally captures multivariate, multimodal output densities and is competitive with recent neural conditional density models and Gaussian processes. To derive the model, we propose a novel approach to the reconstruction of probability densities from their kernel mean embeddings by drawing connections to estimation of Radon-Nikodym derivatives in the reproducing kernel Hilbert space (RKHS). We prove finite sample error bounds which are independent of problem dimensionality. Furthermore, the resulting conditional density model is applied to real-world data and we demonstrate its versatility and competitive performance.

A kernel-based approach to molecular conformation analysis

We present a novel machine learning approach to understanding conformation dynamics of biomolecules. The approach combines kernel-based techniques that are popular in the machine learning community with transfer operator theory for analyzing dynamical systems in order to identify conformation dynamics based on molecular dynamics simulation data. We show that many of the prominent methods like Markov State Models, EDMD, and TICA can be regarded as special cases of this approach and that new efficient algorithms can be constructed based on this derivation. The results of these new powerful methods will be illustrated with several examples, in particular the alanine dipeptide and the protein NTL9.

Singular Value Decomposition of Operators on Reproducing Kernel Hilbert Spaces

Reproducing kernel Hilbert spaces (RKHSs) play an important role in many statistics and machine learning applications ranging from support vector machines to Gaussian processes and kernel embeddings of distributions. Operators acting on such spaces are, for instance, required to embed conditional probability distributions in order to implement the kernel Bayes rule and build sequential data models. It was recently shown that transfer operators such as the Perron-Frobenius or Koopman operator can also be approximated in a similar fashion using covariance and cross-covariance operators and that eigenfunctions of these operators can be obtained by solving associated matrix eigenvalue problems. The goal of this paper is to provide a solid functional analytic foundation for the eigenvalue decomposition of RKHS operators and to extend the approach to the singular value decomposition. The results are illustrated with simple guiding examples.

Markov Chain Importance Sampling - a highly efficient estimator for MCMC

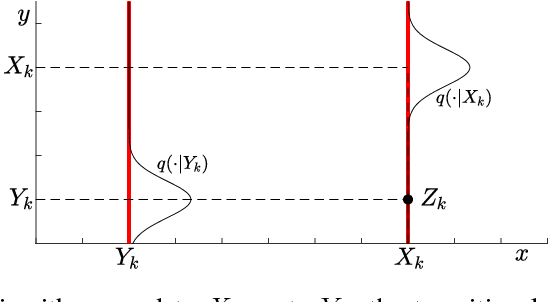
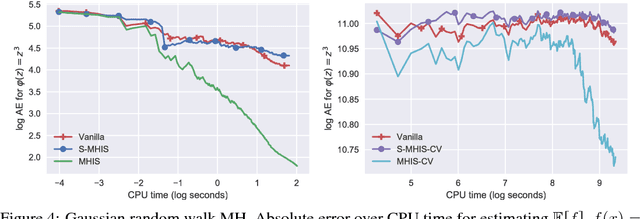
Markov chain algorithms are ubiquitous in machine learning and statistics and many other disciplines. In this work we present a novel estimator applicable to several classes of Markov chains, dubbed Markov chain importance sampling (MCIS). For a broad class of Metropolis-Hastings algorithms, MCIS efficiently makes use of rejected proposals. For discretized Langevin diffusions, it provides a novel way of correcting the discretization error. Our estimator satisfies a central limit theorem and improves on error per CPU cycle, often to a large extent. As a by-product it enables estimating the normalizing constant, an important quantity in Bayesian machine learning and statistics.

Eigendecompositions of Transfer Operators in Reproducing Kernel Hilbert Spaces

Transfer operators such as the Perron--Frobenius or Koopman operator play an important role in the global analysis of complex dynamical systems. The eigenfunctions of these operators can be used to detect metastable sets, to project the dynamics onto the dominant slow processes, or to separate superimposed signals. We extend transfer operator theory to reproducing kernel Hilbert spaces and show that these operators are related to Hilbert space representations of conditional distributions, known as conditional mean embeddings in the machine learning community. Moreover, numerical methods to compute empirical estimates of these embeddings are akin to data-driven methods for the approximation of transfer operators such as extended dynamic mode decomposition and its variants. One main benefit of the presented kernel-based approaches is that these methods can be applied to any domain where a similarity measure given by a kernel is available. We illustrate the results with the aid of guiding examples and highlight potential applications in molecular dynamics as well as video and text data analysis.