The linear conditional expectation in Hilbert space

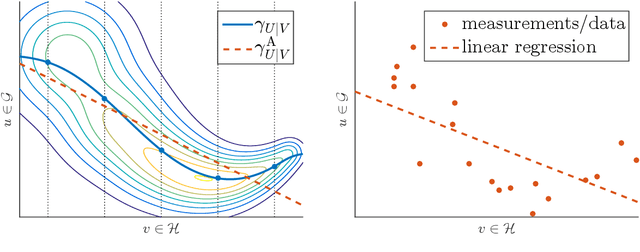
The linear conditional expectation (LCE) provides a best linear (or rather, affine) estimate of the conditional expectation and hence plays an important r\^ole in approximate Bayesian inference, especially the Bayes linear approach. This article establishes the analytical properties of the LCE in an infinite-dimensional Hilbert space context. In addition, working in the space of affine Hilbert--Schmidt operators, we establish a regularisation procedure for this LCE. As an important application, we obtain a simple alternative derivation and intuitive justification of the conditional mean embedding formula, a concept widely used in machine learning to perform the conditioning of random variables by embedding them into reproducing kernel Hilbert spaces.

A Rigorous Theory of Conditional Mean Embeddings

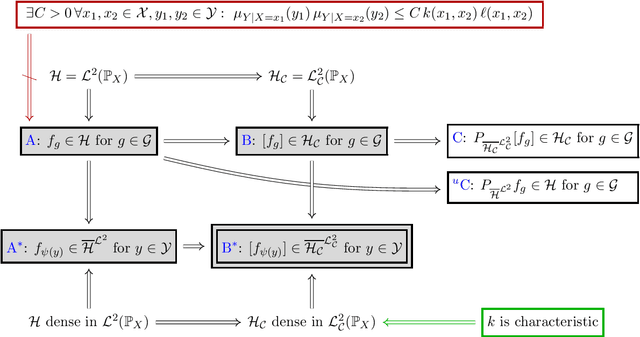
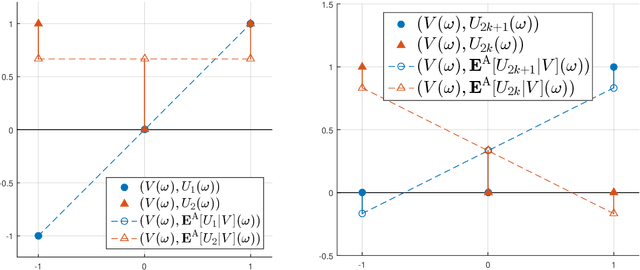
Conditional mean embeddings (CME) have proven themselves to be a powerful tool in many machine learning applications. They allow the efficient conditioning of probability distributions within the corresponding reproducing kernel Hilbert spaces (RKHSs) by providing a linear-algebraic relation for the kernel mean embeddings of the respective probability distributions. Both centered and uncentered covariance operators have been used to define CMEs in the existing literature. In this paper, we develop a mathematically rigorous theory for both variants, discuss the merits and problems of either, and significantly weaken the conditions for applicability of CMEs. In the course of this, we demonstrate a beautiful connection to Gaussian conditioning in Hilbert spaces.

Markov Chain Importance Sampling - a highly efficient estimator for MCMC

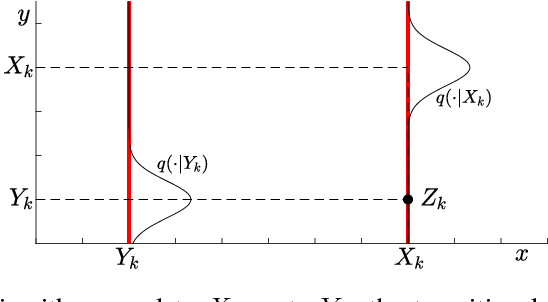
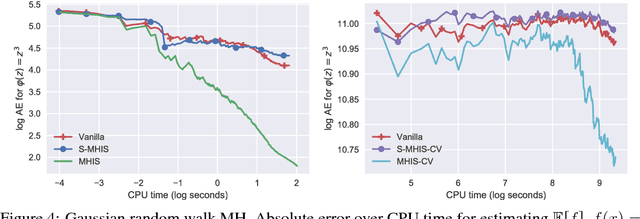
Markov chain algorithms are ubiquitous in machine learning and statistics and many other disciplines. In this work we present a novel estimator applicable to several classes of Markov chains, dubbed Markov chain importance sampling (MCIS). For a broad class of Metropolis-Hastings algorithms, MCIS efficiently makes use of rejected proposals. For discretized Langevin diffusions, it provides a novel way of correcting the discretization error. Our estimator satisfies a central limit theorem and improves on error per CPU cycle, often to a large extent. As a by-product it enables estimating the normalizing constant, an important quantity in Bayesian machine learning and statistics.