Geometric convergence of elliptical slice sampling

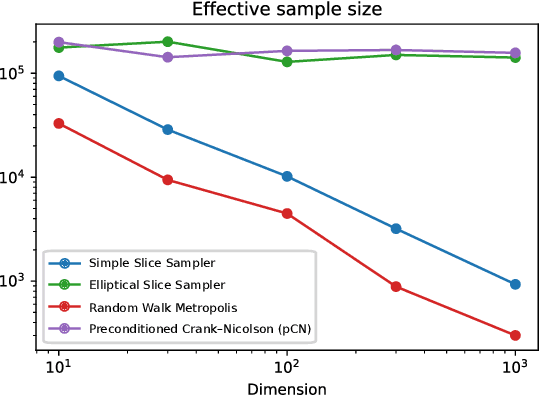
For Bayesian learning, given likelihood function and Gaussian prior, the elliptical slice sampler, introduced by Murray, Adams and MacKay 2010, provides a tool for the construction of a Markov chain for approximate sampling of the underlying posterior distribution. Besides of its wide applicability and simplicity its main feature is that no tuning is necessary. Under weak regularity assumptions on the posterior density we show that the corresponding Markov chain is geometrically ergodic and therefore yield qualitative convergence guarantees. We illustrate our result for Gaussian posteriors as they appear in Gaussian process regression, as well as in a setting of a multi-modal distribution. Remarkably, our numerical experiments indicate a dimension-independent performance of elliptical slice sampling even in situations where our ergodicity result does not apply.

The linear conditional expectation in Hilbert space

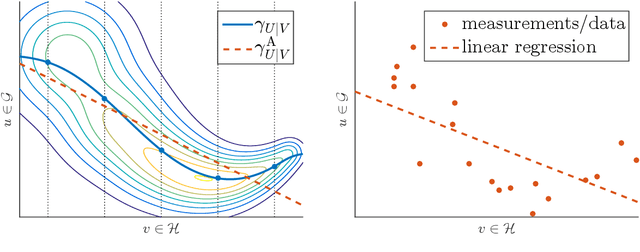
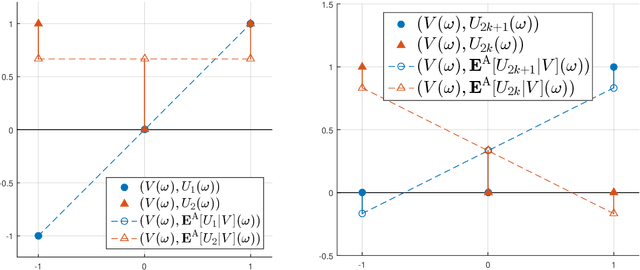
The linear conditional expectation (LCE) provides a best linear (or rather, affine) estimate of the conditional expectation and hence plays an important r\^ole in approximate Bayesian inference, especially the Bayes linear approach. This article establishes the analytical properties of the LCE in an infinite-dimensional Hilbert space context. In addition, working in the space of affine Hilbert--Schmidt operators, we establish a regularisation procedure for this LCE. As an important application, we obtain a simple alternative derivation and intuitive justification of the conditional mean embedding formula, a concept widely used in machine learning to perform the conditioning of random variables by embedding them into reproducing kernel Hilbert spaces.