Parallel Affine Transformation Tuning of Markov Chain Monte Carlo

The performance of Markov chain Monte Carlo samplers strongly depends on the properties of the target distribution such as its covariance structure, the location of its probability mass and its tail behavior. We explore the use of bijective affine transformations of the sample space to improve the properties of the target distribution and thereby the performance of samplers running in the transformed space. In particular, we propose a flexible and user-friendly scheme for adaptively learning the affine transformation during sampling. Moreover, the combination of our scheme with Gibbsian polar slice sampling is shown to produce samples of high quality at comparatively low computational cost in several settings based on real-world data.

Gibbsian polar slice sampling

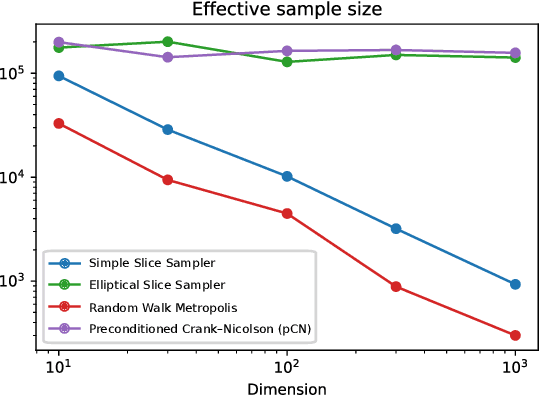
Polar slice sampling (Roberts & Rosenthal, 2002) is a Markov chain approach for approximate sampling of distributions that is difficult, if not impossible, to implement efficiently, but behaves provably well with respect to the dimension. By updating the directional and radial components of chain iterates separately, we obtain a family of samplers that mimic polar slice sampling, and yet can be implemented efficiently. Numerical experiments for a variety of settings indicate that our proposed algorithm outperforms the two most closely related approaches, elliptical slice sampling (Murray et al., 2010) and hit-and-run uniform slice sampling (MacKay, 2003). We prove the well-definedness and convergence of our methods under suitable assumptions on the target distribution.

Reversibility of elliptical slice sampling revisited

We discuss the well-definedness of elliptical slice sampling, a Markov chain approach for approximate sampling of posterior distributions introduced by Murray, Adams and MacKay 2010. We point to a regularity requirement and provide an alternative proof of the reversibility property. In particular, this guarantees the correctness of the slice sampling scheme also on infinite-dimensional separable Hilbert spaces.

Geometric convergence of elliptical slice sampling

For Bayesian learning, given likelihood function and Gaussian prior, the elliptical slice sampler, introduced by Murray, Adams and MacKay 2010, provides a tool for the construction of a Markov chain for approximate sampling of the underlying posterior distribution. Besides of its wide applicability and simplicity its main feature is that no tuning is necessary. Under weak regularity assumptions on the posterior density we show that the corresponding Markov chain is geometrically ergodic and therefore yield qualitative convergence guarantees. We illustrate our result for Gaussian posteriors as they appear in Gaussian process regression, as well as in a setting of a multi-modal distribution. Remarkably, our numerical experiments indicate a dimension-independent performance of elliptical slice sampling even in situations where our ergodicity result does not apply.