The linear conditional expectation in Hilbert space
Paper and Code
Aug 27, 2020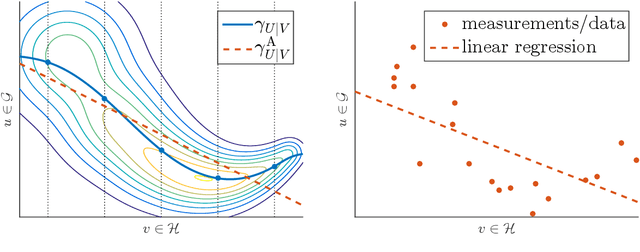


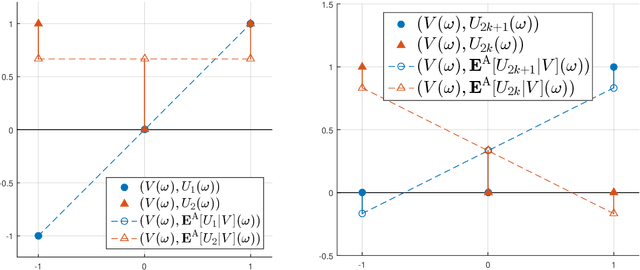
The linear conditional expectation (LCE) provides a best linear (or rather, affine) estimate of the conditional expectation and hence plays an important r\^ole in approximate Bayesian inference, especially the Bayes linear approach. This article establishes the analytical properties of the LCE in an infinite-dimensional Hilbert space context. In addition, working in the space of affine Hilbert--Schmidt operators, we establish a regularisation procedure for this LCE. As an important application, we obtain a simple alternative derivation and intuitive justification of the conditional mean embedding formula, a concept widely used in machine learning to perform the conditioning of random variables by embedding them into reproducing kernel Hilbert spaces.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge