Autoregressive Denoising Diffusion Models for Multivariate Probabilistic Time Series Forecasting

In this work, we propose \texttt{TimeGrad}, an autoregressive model for multivariate probabilistic time series forecasting which samples from the data distribution at each time step by estimating its gradient. To this end, we use diffusion probabilistic models, a class of latent variable models closely connected to score matching and energy-based methods. Our model learns gradients by optimizing a variational bound on the data likelihood and at inference time converts white noise into a sample of the distribution of interest through a Markov chain using Langevin sampling. We demonstrate experimentally that the proposed autoregressive denoising diffusion model is the new state-of-the-art multivariate probabilistic forecasting method on real-world data sets with thousands of correlated dimensions. We hope that this method is a useful tool for practitioners and lays the foundation for future research in this area.

Disentangling Multiple Conditional Inputs in GANs

In this paper, we propose a method that disentangles the effects of multiple input conditions in Generative Adversarial Networks (GANs). In particular, we demonstrate our method in controlling color, texture, and shape of a generated garment image for computer-aided fashion design. To disentangle the effect of input attributes, we customize conditional GANs with consistency loss functions. In our experiments, we tune one input at a time and show that we can guide our network to generate novel and realistic images of clothing articles. In addition, we present a fashion design process that estimates the input attributes of an existing garment and modifies them using our generator.

First Order Generative Adversarial Networks

GANs excel at learning high dimensional distributions, but they can update generator parameters in directions that do not correspond to the steepest descent direction of the objective. Prominent examples of problematic update directions include those used in both Goodfellow's original GAN and the WGAN-GP. To formally describe an optimal update direction, we introduce a theoretical framework which allows the derivation of requirements on both the divergence and corresponding method for determining an update direction, with these requirements guaranteeing unbiased mini-batch updates in the direction of steepest descent. We propose a novel divergence which approximates the Wasserstein distance while regularizing the critic's first order information. Together with an accompanying update direction, this divergence fulfills the requirements for unbiased steepest descent updates. We verify our method, the First Order GAN, with image generation on CelebA, LSUN and CIFAR-10 and set a new state of the art on the One Billion Word language generation task. Code to reproduce experiments is available.

Coulomb GANs: Provably Optimal Nash Equilibria via Potential Fields

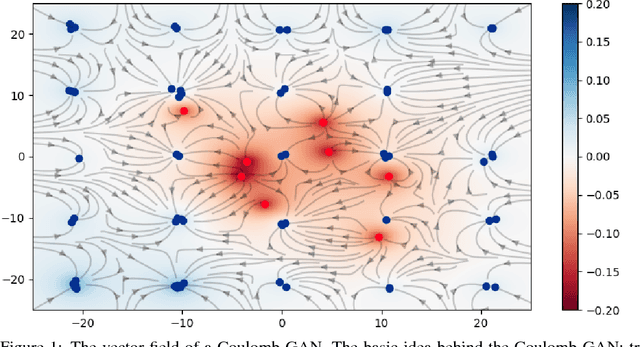
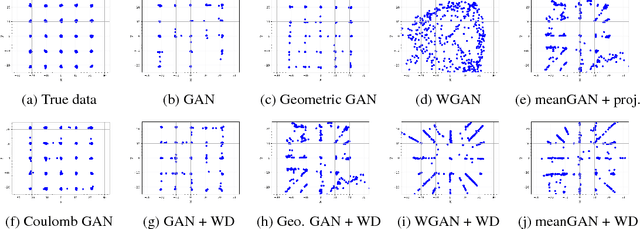
Generative adversarial networks (GANs) evolved into one of the most successful unsupervised techniques for generating realistic images. Even though it has recently been shown that GAN training converges, GAN models often end up in local Nash equilibria that are associated with mode collapse or otherwise fail to model the target distribution. We introduce Coulomb GANs, which pose the GAN learning problem as a potential field of charged particles, where generated samples are attracted to training set samples but repel each other. The discriminator learns a potential field while the generator decreases the energy by moving its samples along the vector (force) field determined by the gradient of the potential field. Through decreasing the energy, the GAN model learns to generate samples according to the whole target distribution and does not only cover some of its modes. We prove that Coulomb GANs possess only one Nash equilibrium which is optimal in the sense that the model distribution equals the target distribution. We show the efficacy of Coulomb GANs on a variety of image datasets. On LSUN and celebA, Coulomb GANs set a new state of the art and produce a previously unseen variety of different samples.

GANosaic: Mosaic Creation with Generative Texture Manifolds

This paper presents a novel framework for generating texture mosaics with convolutional neural networks. Our method is called GANosaic and performs optimization in the latent noise space of a generative texture model, which allows the transformation of a content image into a mosaic exhibiting the visual properties of the underlying texture manifold. To represent that manifold, we use a state-of-the-art generative adversarial method for texture synthesis, which can learn expressive texture representations from data and produce mosaic images with very high resolution. This fully convolutional model generates smooth (without any visible borders) mosaic images which morph and blend different textures locally. In addition, we develop a new type of differentiable statistical regularization appropriate for optimization over the prior noise space of the PSGAN model.