Gideon Dresdner
Probabilistic Precipitation Downscaling with Optical Flow-Guided Diffusion
Dec 11, 2023Abstract:In climate science and meteorology, local precipitation predictions are limited by the immense computational costs induced by the high spatial resolution that simulation methods require. A common workaround is statistical downscaling (aka superresolution), where a low-resolution prediction is super-resolved using statistical approaches. While traditional computer vision tasks mainly focus on human perception or mean squared error, applications in weather and climate require capturing the conditional distribution of high-resolution patterns given low-resolution patterns so that reliable ensemble averages can be taken. Our approach relies on extending recent video diffusion models to precipitation superresolution: an optical flow on the high-resolution output induces temporally coherent predictions, whereas a temporally-conditioned diffusion model generates residuals that capture the correct noise characteristics and high-frequency patterns. We test our approach on X-SHiELD, an established large-scale climate simulation dataset, and compare against two state-of-the-art baselines, focusing on CRPS, MSE, precipitation distributions, as well as an illustrative case -- the complex terrain of California. Our approach sets a new standard for data-driven precipitation downscaling.
ACE: A fast, skillful learned global atmospheric model for climate prediction
Oct 03, 2023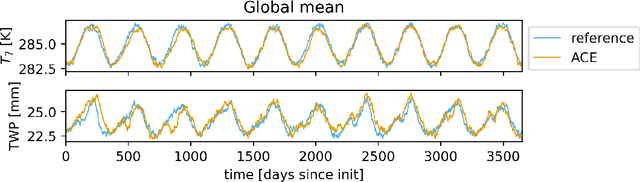
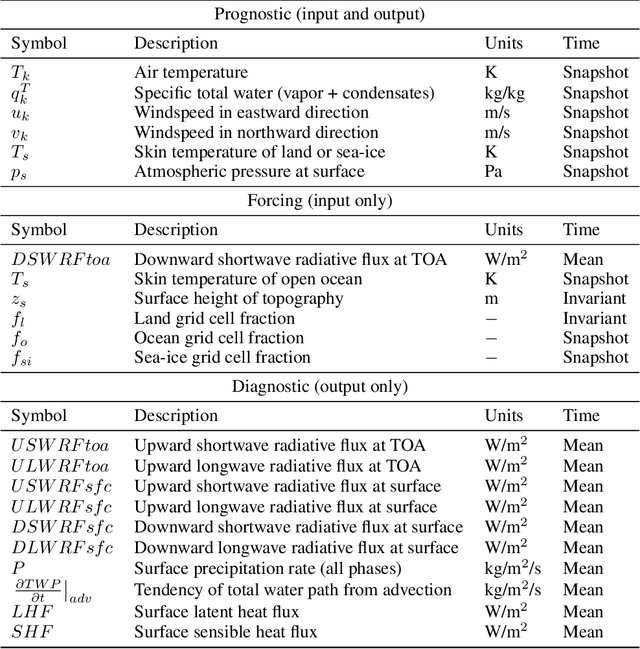


Abstract:Existing ML-based atmospheric models are not suitable for climate prediction, which requires long-term stability and physical consistency. We present ACE (AI2 Climate Emulator), a 200M-parameter, autoregressive machine learning emulator of an existing comprehensive 100-km resolution global atmospheric model. The formulation of ACE allows evaluation of physical laws such as the conservation of mass and moisture. The emulator is stable for 10 years, nearly conserves column moisture without explicit constraints and faithfully reproduces the reference model's climate, outperforming a challenging baseline on over 80% of tracked variables. ACE requires nearly 100x less wall clock time and is 100x more energy efficient than the reference model using typically available resources.
Learning to correct spectral methods for simulating turbulent flows
Jul 01, 2022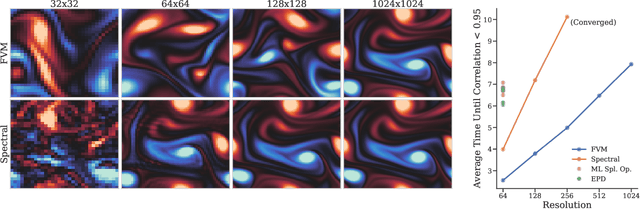
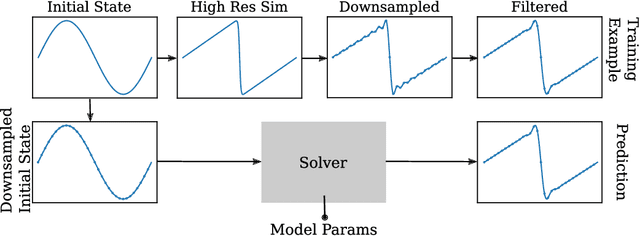
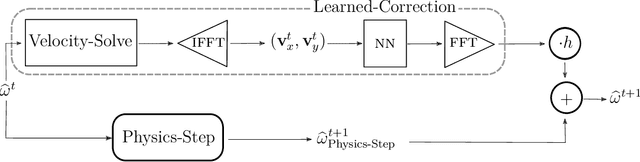

Abstract:Despite their ubiquity throughout science and engineering, only a handful of partial differential equations (PDEs) have analytical, or closed-form solutions. This motivates a vast amount of classical work on numerical simulation of PDEs and more recently, a whirlwind of research into data-driven techniques leveraging machine learning (ML). A recent line of work indicates that a hybrid of classical numerical techniques with machine learning can offer significant improvements over either approach alone. In this work, we show that the choice of the numerical scheme is crucial when incorporating physics-based priors. We build upon Fourier-based spectral methods, which are considerably more efficient than other numerical schemes for simulating PDEs with smooth and periodic solutions. Specifically, we develop ML-augmented spectral solvers for three model PDEs of fluid dynamics, which improve upon the accuracy of standard spectral solvers at the same resolution. We also demonstrate a handful of key design principles for combining machine learning and numerical methods for solving PDEs.
Faster One-Sample Stochastic Conditional Gradient Method for Composite Convex Minimization
Feb 26, 2022



Abstract:We propose a stochastic conditional gradient method (CGM) for minimizing convex finite-sum objectives formed as a sum of smooth and non-smooth terms. Existing CGM variants for this template either suffer from slow convergence rates, or require carefully increasing the batch size over the course of the algorithm's execution, which leads to computing full gradients. In contrast, the proposed method, equipped with a stochastic average gradient (SAG) estimator, requires only one sample per iteration. Nevertheless, it guarantees fast convergence rates on par with more sophisticated variance reduction techniques. In applications we put special emphasis on problems with a large number of separable constraints. Such problems are prevalent among semidefinite programming (SDP) formulations arising in machine learning and theoretical computer science. We provide numerical experiments on matrix completion, unsupervised clustering, and sparsest-cut SDPs.
Neighborhood Contrastive Learning Applied to Online Patient Monitoring
Jun 09, 2021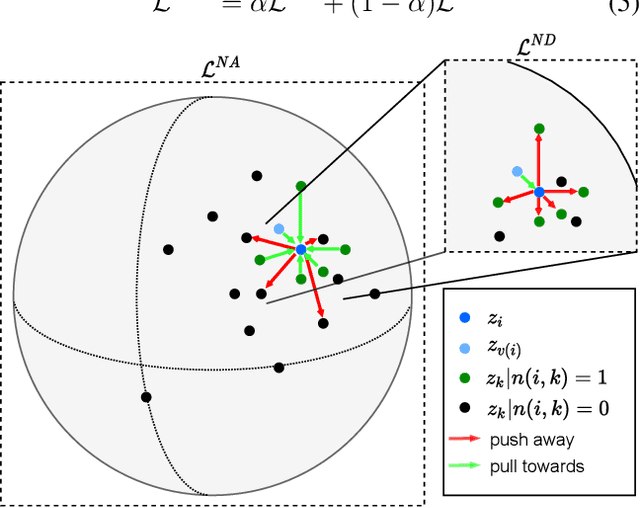
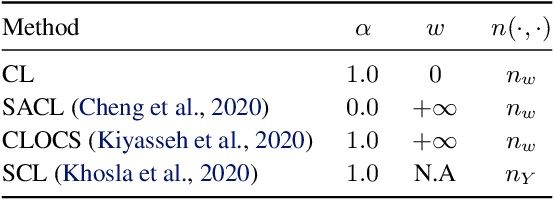
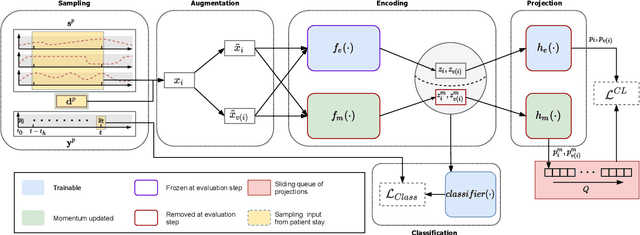
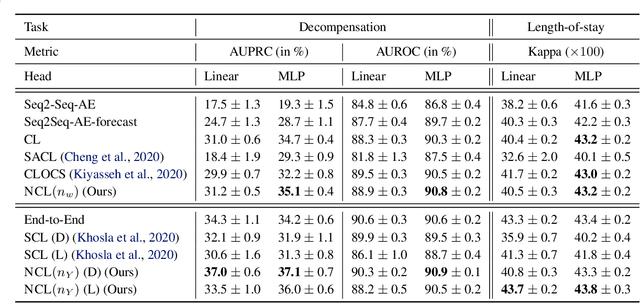
Abstract:Intensive care units (ICU) are increasingly looking towards machine learning for methods to provide online monitoring of critically ill patients. In machine learning, online monitoring is often formulated as a supervised learning problem. Recently, contrastive learning approaches have demonstrated promising improvements over competitive supervised benchmarks. These methods rely on well-understood data augmentation techniques developed for image data which do not apply to online monitoring. In this work, we overcome this limitation by supplementing time-series data augmentation techniques with a novel contrastive learning objective which we call neighborhood contrastive learning (NCL). Our objective explicitly groups together contiguous time segments from each patient while maintaining state-specific information. Our experiments demonstrate a marked improvement over existing work applying contrastive methods to medical time-series.
Boosting Variational Inference With Locally Adaptive Step-Sizes
May 19, 2021



Abstract:Variational Inference makes a trade-off between the capacity of the variational family and the tractability of finding an approximate posterior distribution. Instead, Boosting Variational Inference allows practitioners to obtain increasingly good posterior approximations by spending more compute. The main obstacle to widespread adoption of Boosting Variational Inference is the amount of resources necessary to improve over a strong Variational Inference baseline. In our work, we trace this limitation back to the global curvature of the KL-divergence. We characterize how the global curvature impacts time and memory consumption, address the problem with the notion of local curvature, and provide a novel approximate backtracking algorithm for estimating local curvature. We give new theoretical convergence rates for our algorithms and provide experimental validation on synthetic and real-world datasets.
Stochastic Frank-Wolfe for Constrained Finite-Sum Minimization
Feb 29, 2020
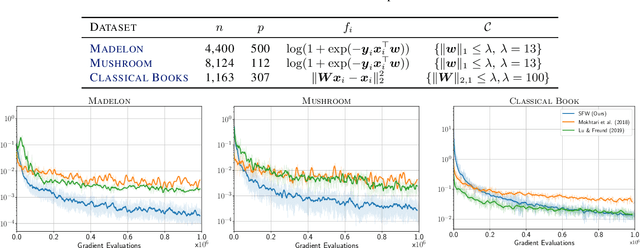

Abstract:We propose a novel Stochastic Frank-Wolfe (a.k.a. Conditional Gradient) algorithm with a fixed batch size tailored to the constrained optimization of a finite sum of smooth objectives. The design of our method hinges on a primal-dual interpretation of the Frank-Wolfe algorithm. Recent work to design stochastic variants of the Frank-Wolfe algorithm falls into two categories: algorithms with increasing batch size, and algorithms with a given, constant, batch size. The former have faster convergence rates but are impractical; the latter are practical but slower. The proposed method combines the advantages of both: it converges for unit batch size, and has faster theoretical worst-case rates than previous unit batch size algorithms. Our experiments also show faster empirical convergence than previous unit batch size methods for several tasks. Finally, we construct a stochastic estimator of the Frank-Wolfe gap. It allows us to bound the true Frank-Wolfe gap, which in the convex setting bounds the primal-dual gap in the convex case while in general is a measure of stationarity. Our gap estimator can therefore be used as a practical stopping criterion in all cases.
Boosting Black Box Variational Inference
Nov 01, 2018


Abstract:Approximating a probability density in a tractable manner is a central task in Bayesian statistics. Variational Inference (VI) is a popular technique that achieves tractability by choosing a relatively simple variational family. Borrowing ideas from the classic boosting framework, recent approaches attempt to \emph{boost} VI by replacing the selection of a single density with a greedily constructed mixture of densities. In order to guarantee convergence, previous works impose stringent assumptions that require significant effort for practitioners. Specifically, they require a custom implementation of the greedy step (called the LMO) for every probabilistic model with respect to an unnatural variational family of truncated distributions. Our work fixes these issues with novel theoretical and algorithmic insights. On the theoretical side, we show that boosting VI satisfies a relaxed smoothness assumption which is sufficient for the convergence of the functional Frank-Wolfe (FW) algorithm. Furthermore, we rephrase the LMO problem and propose to maximize the Residual ELBO (RELBO) which replaces the standard ELBO optimization in VI. These theoretical enhancements allow for black box implementation of the boosting subroutine. Finally, we present a stopping criterion drawn from the duality gap in the classic FW analyses and exhaustive experiments to illustrate the usefulness of our theoretical and algorithmic contributions.
Scalable Gaussian Processes on Discrete Domains
Oct 24, 2018



Abstract:Kernel methods on discrete domains have shown great promise for many challenging tasks, e.g., on biological sequence data as well as on molecular structures. Scalable kernel methods like support vector machines offer good predictive performances but they often do not provide uncertainty estimates. In contrast, probabilistic kernel methods like Gaussian Processes offer uncertainty estimates in addition to good predictive performance but fall short in terms of scalability. We present the first sparse Gaussian Process approximation framework on discrete input domains. Our framework achieves good predictive performance as well as uncertainty estimates using different discrete optimization techniques. We present competitive results comparing our framework to support vector machine and full Gaussian Process baselines on synthetic data as well as on challenging real-world DNA sequence data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge