Probabilistic Forecasting with Coherent Aggregation

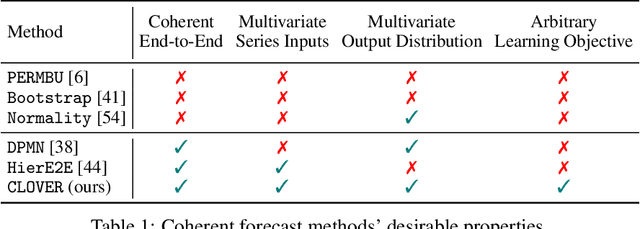
Obtaining accurate probabilistic forecasts while respecting hierarchical information is an important operational challenge in many applications, perhaps most obviously in energy management, supply chain planning, and resource allocation. The basic challenge, especially for multivariate forecasting, is that forecasts are often required to be coherent with respect to the hierarchical structure. In this paper, we propose a new model which leverages a factor model structure to produce coherent forecasts by construction. This is a consequence of a simple (exchangeability) observation: permuting \textit{}base-level series in the hierarchy does not change their aggregates. Our model uses a convolutional neural network to produce parameters for the factors, their loadings and base-level distributions; it produces samples which can be differentiated with respect to the model's parameters; and it can therefore optimize for any sample-based loss function, including the Continuous Ranked Probability Score and quantile losses. We can choose arbitrary continuous distributions for the factor and the base-level distributions. We compare our method to two previous methods which can be optimized end-to-end, while enforcing coherent aggregation. Our model achieves significant improvements: between $11.8-41.4\%$ on three hierarchical forecasting datasets. We also analyze the influence of parameters in our model with respect to base-level distribution and number of factors.

Learning differentiable solvers for systems with hard constraints

We introduce a practical method to enforce linear partial differential equation (PDE) constraints for functions defined by neural networks (NNs), up to a desired tolerance. By combining methods in differentiable physics and applications of the implicit function theorem to NN models, we develop a differentiable PDE-constrained NN layer. During training, our model learns a family of functions, each of which defines a mapping from PDE parameters to PDE solutions. At inference time, the model finds an optimal linear combination of the functions in the learned family by solving a PDE-constrained optimization problem. Our method provides continuous solutions over the domain of interest that exactly satisfy desired physical constraints. Our results show that incorporating hard constraints directly into the NN architecture achieves much lower test error, compared to training on an unconstrained objective.

Stochastic Frank-Wolfe for Constrained Finite-Sum Minimization

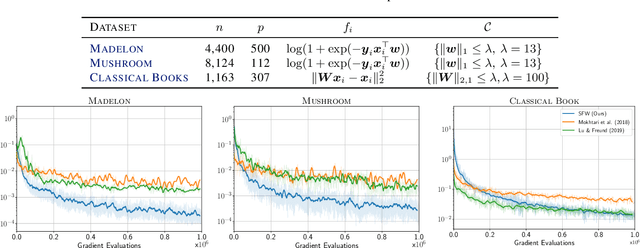
We propose a novel Stochastic Frank-Wolfe (a.k.a. Conditional Gradient) algorithm with a fixed batch size tailored to the constrained optimization of a finite sum of smooth objectives. The design of our method hinges on a primal-dual interpretation of the Frank-Wolfe algorithm. Recent work to design stochastic variants of the Frank-Wolfe algorithm falls into two categories: algorithms with increasing batch size, and algorithms with a given, constant, batch size. The former have faster convergence rates but are impractical; the latter are practical but slower. The proposed method combines the advantages of both: it converges for unit batch size, and has faster theoretical worst-case rates than previous unit batch size algorithms. Our experiments also show faster empirical convergence than previous unit batch size methods for several tasks. Finally, we construct a stochastic estimator of the Frank-Wolfe gap. It allows us to bound the true Frank-Wolfe gap, which in the convex setting bounds the primal-dual gap in the convex case while in general is a measure of stationarity. Our gap estimator can therefore be used as a practical stopping criterion in all cases.