Zero-shot Forecasting by Simulation Alone

Zero-shot time-series forecasting holds great promise, but is still in its infancy, hindered by limited and biased data corpora, leakage-prone evaluation, and privacy and licensing constraints. Motivated by these challenges, we propose the first practical univariate time series simulation pipeline which is simultaneously fast enough for on-the-fly data generation and enables notable zero-shot forecasting performance on M-Series and GiftEval benchmarks that capture trend/seasonality/intermittency patterns, typical of industrial forecasting applications across a variety of domains. Our simulator, which we call SarSim0 (SARIMA Simulator for Zero-Shot Forecasting), is based off of a seasonal autoregressive integrated moving average (SARIMA) model as its core data source. Due to instability in the autoregressive component, naive SARIMA simulation often leads to unusable paths. Instead, we follow a three-step procedure: (1) we sample well-behaved trajectories from its characteristic polynomial stability region; (2) we introduce a superposition scheme that combines multiple paths into rich multi-seasonality traces; and (3) we add rate-based heavy-tailed noise models to capture burstiness and intermittency alongside seasonalities and trends. SarSim0 is orders of magnitude faster than kernel-based generators, and it enables training on circa 1B unique purely simulated series, generated on the fly; after which well-established neural network backbones exhibit strong zero-shot generalization, surpassing strong statistical forecasters and recent foundation baselines, while operating under strict zero-shot protocol. Notably, on GiftEval we observe a "student-beats-teacher" effect: models trained on our simulations exceed the forecasting accuracy of the AutoARIMA generating processes.

Forking-Sequences

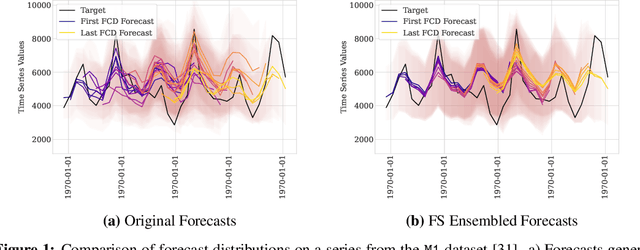
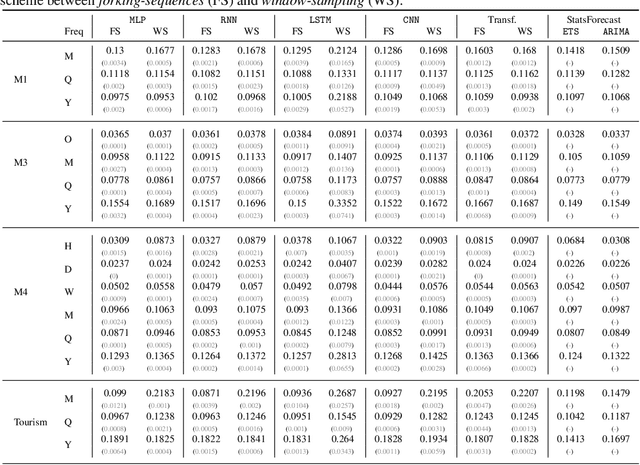
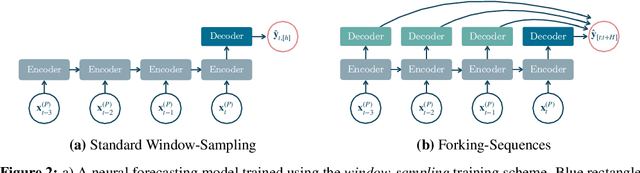
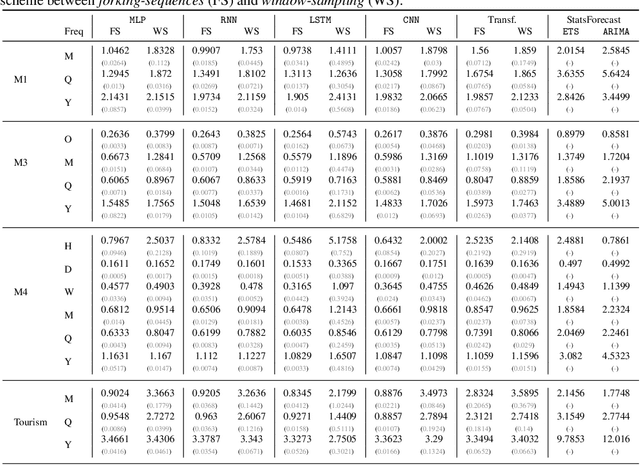
While accuracy is a critical requirement for time series forecasting models, an equally important (yet often overlooked) desideratum is forecast stability across forecast creation dates (FCDs). Even highly accurate models can produce erratic revisions between FCDs, undermining stakeholder trust and disrupting downstream decision-making. To improve forecast stability, models like MQCNN, MQT, and SPADE employ a little-known but highly effective technique: forking-sequences. Unlike standard statistical and neural forecasting methods that treat each FCD independently, the forking-sequences method jointly encodes and decodes the entire time series across all FCDs, in a way mirroring time series cross-validation. Since forking sequences remains largely unknown in the broader neural forecasting community, in this work, we formalize the forking-sequences approach, and we make a case for its broader adoption. We demonstrate three key benefits of forking-sequences: (i) more stable and consistent gradient updates during training; (ii) reduced forecast variance through ensembling; and (iii) improved inference computational efficiency. We validate forking-sequences' benefits using 16 datasets from the M1, M3, M4, and Tourism competitions, showing improvements in forecast percentage change stability of 28.8%, 28.8%, 37.9%, and 31.3%, and 8.8%, on average, for MLP, RNN, LSTM, CNN, and Transformer-based architectures, respectively.

Probabilistic Forecasting with Coherent Aggregation

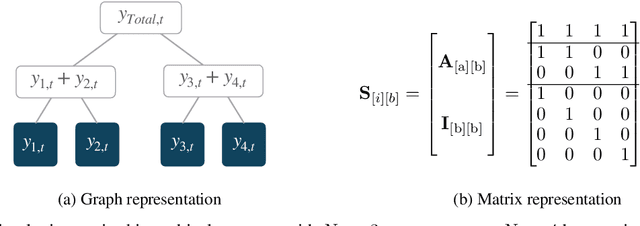
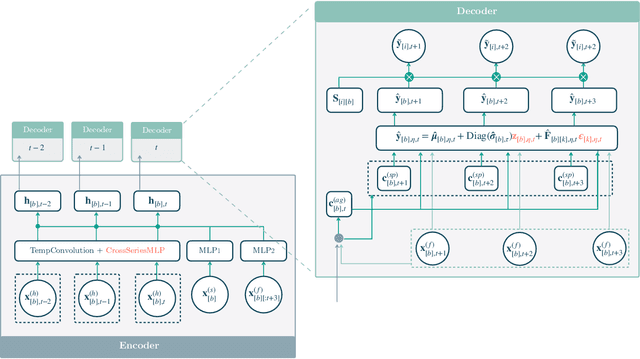
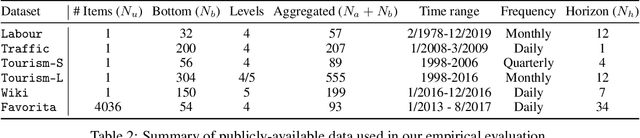
Obtaining accurate probabilistic forecasts while respecting hierarchical information is an important operational challenge in many applications, perhaps most obviously in energy management, supply chain planning, and resource allocation. The basic challenge, especially for multivariate forecasting, is that forecasts are often required to be coherent with respect to the hierarchical structure. In this paper, we propose a new model which leverages a factor model structure to produce coherent forecasts by construction. This is a consequence of a simple (exchangeability) observation: permuting \textit{}base-level series in the hierarchy does not change their aggregates. Our model uses a convolutional neural network to produce parameters for the factors, their loadings and base-level distributions; it produces samples which can be differentiated with respect to the model's parameters; and it can therefore optimize for any sample-based loss function, including the Continuous Ranked Probability Score and quantile losses. We can choose arbitrary continuous distributions for the factor and the base-level distributions. We compare our method to two previous methods which can be optimized end-to-end, while enforcing coherent aggregation. Our model achieves significant improvements: between $11.8-41.4\%$ on three hierarchical forecasting datasets. We also analyze the influence of parameters in our model with respect to base-level distribution and number of factors.

Probabilistic Hierarchical Forecasting with Deep Poisson Mixtures

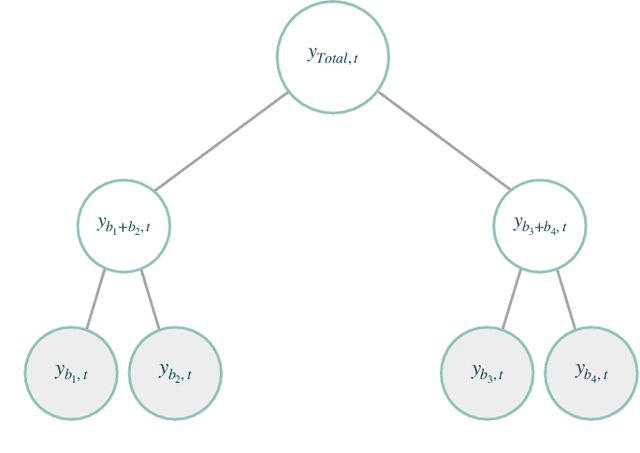
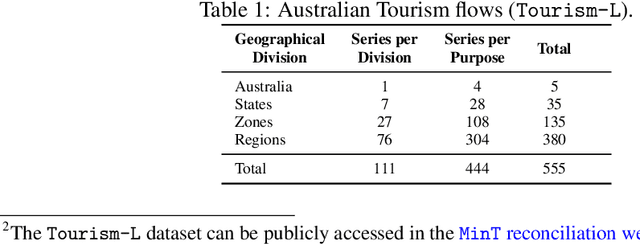
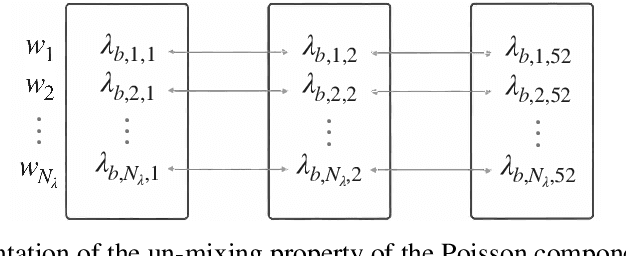
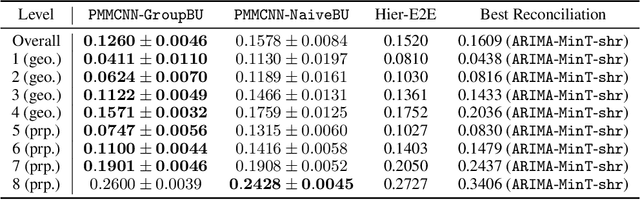
Hierarchical forecasting problems arise when time series compose a group structure that naturally defines aggregation and disaggregation coherence constraints for the predictions. In this work, we explore a new forecast representation, the Poisson Mixture Mesh (PMM), that can produce probabilistic, coherent predictions; it is compatible with the neural forecasting innovations, and defines simple aggregation and disaggregation rules capable of accommodating hierarchical structures, unknown during its optimization. We performed an empirical evaluation to compare the PMM to other hierarchical forecasting methods on Australian domestic tourism data, where we obtain a 20 percent relative improvement.