Probabilistic Forecasting with Coherent Aggregation
Paper and Code
Jul 19, 2023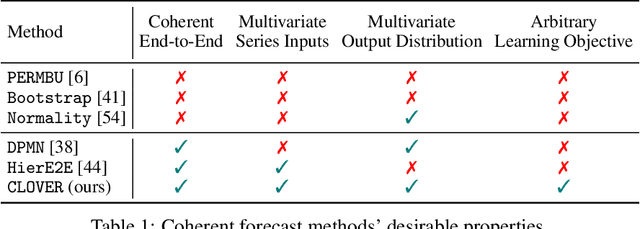
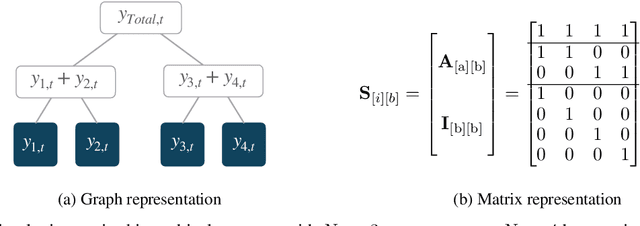
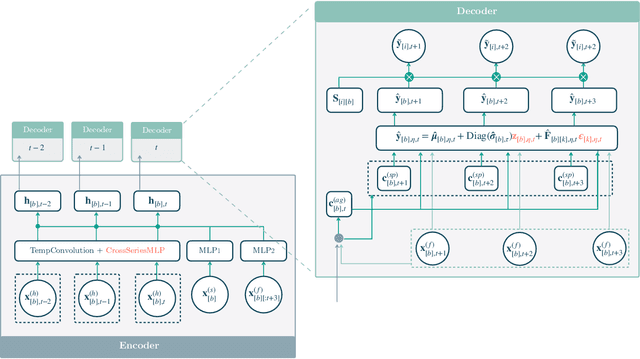
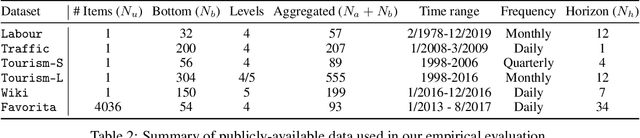
Obtaining accurate probabilistic forecasts while respecting hierarchical information is an important operational challenge in many applications, perhaps most obviously in energy management, supply chain planning, and resource allocation. The basic challenge, especially for multivariate forecasting, is that forecasts are often required to be coherent with respect to the hierarchical structure. In this paper, we propose a new model which leverages a factor model structure to produce coherent forecasts by construction. This is a consequence of a simple (exchangeability) observation: permuting \textit{}base-level series in the hierarchy does not change their aggregates. Our model uses a convolutional neural network to produce parameters for the factors, their loadings and base-level distributions; it produces samples which can be differentiated with respect to the model's parameters; and it can therefore optimize for any sample-based loss function, including the Continuous Ranked Probability Score and quantile losses. We can choose arbitrary continuous distributions for the factor and the base-level distributions. We compare our method to two previous methods which can be optimized end-to-end, while enforcing coherent aggregation. Our model achieves significant improvements: between $11.8-41.4\%$ on three hierarchical forecasting datasets. We also analyze the influence of parameters in our model with respect to base-level distribution and number of factors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge