Jamie A. Smith
Learning to correct spectral methods for simulating turbulent flows
Jul 01, 2022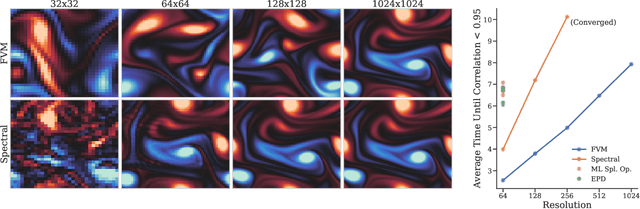
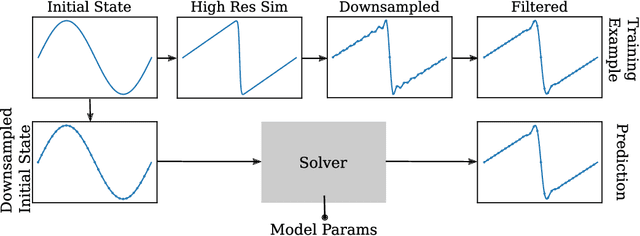

Abstract:Despite their ubiquity throughout science and engineering, only a handful of partial differential equations (PDEs) have analytical, or closed-form solutions. This motivates a vast amount of classical work on numerical simulation of PDEs and more recently, a whirlwind of research into data-driven techniques leveraging machine learning (ML). A recent line of work indicates that a hybrid of classical numerical techniques with machine learning can offer significant improvements over either approach alone. In this work, we show that the choice of the numerical scheme is crucial when incorporating physics-based priors. We build upon Fourier-based spectral methods, which are considerably more efficient than other numerical schemes for simulating PDEs with smooth and periodic solutions. Specifically, we develop ML-augmented spectral solvers for three model PDEs of fluid dynamics, which improve upon the accuracy of standard spectral solvers at the same resolution. We also demonstrate a handful of key design principles for combining machine learning and numerical methods for solving PDEs.
Variational Data Assimilation with a Learned Inverse Observation Operator
Feb 22, 2021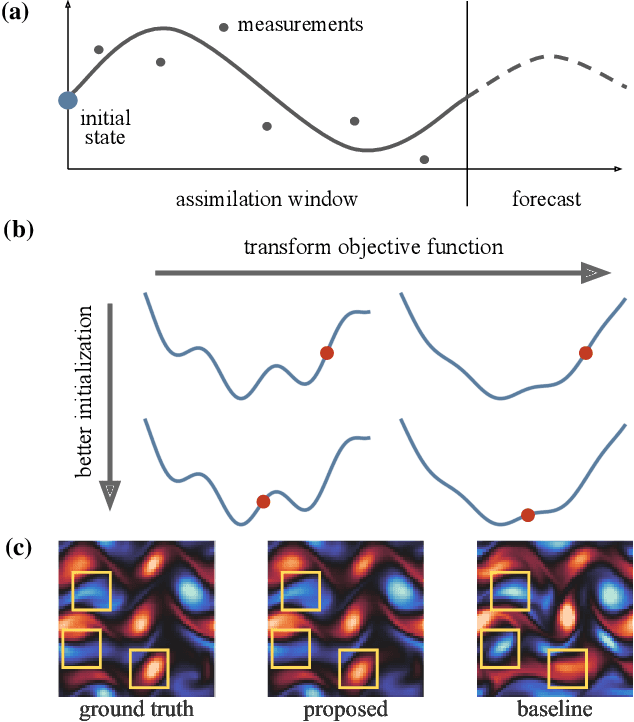
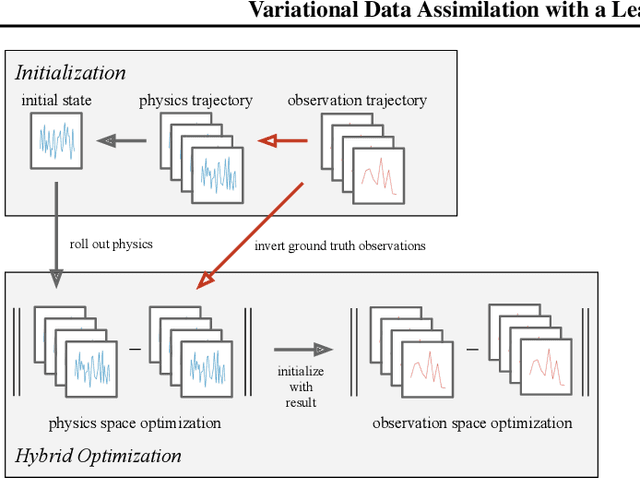

Abstract:Variational data assimilation optimizes for an initial state of a dynamical system such that its evolution fits observational data. The physical model can subsequently be evolved into the future to make predictions. This principle is a cornerstone of large scale forecasting applications such as numerical weather prediction. As such, it is implemented in current operational systems of weather forecasting agencies across the globe. However, finding a good initial state poses a difficult optimization problem in part due to the non-invertible relationship between physical states and their corresponding observations. We learn a mapping from observational data to physical states and show how it can be used to improve optimizability. We employ this mapping in two ways: to better initialize the non-convex optimization problem, and to reformulate the objective function in better behaved physics space instead of observation space. Our experimental results for the Lorenz96 model and a two-dimensional turbulent fluid flow demonstrate that this procedure significantly improves forecast quality for chaotic systems.
Machine learning accelerated computational fluid dynamics
Jan 28, 2021



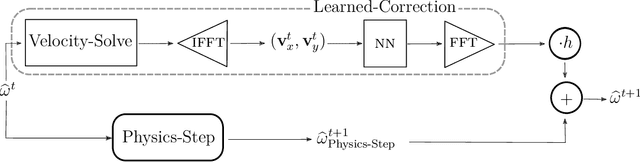
Abstract:Numerical simulation of fluids plays an essential role in modeling many physical phenomena, such as weather, climate, aerodynamics and plasma physics. Fluids are well described by the Navier-Stokes equations, but solving these equations at scale remains daunting, limited by the computational cost of resolving the smallest spatiotemporal features. This leads to unfavorable trade-offs between accuracy and tractability. Here we use end-to-end deep learning to improve approximations inside computational fluid dynamics for modeling two-dimensional turbulent flows. For both direct numerical simulation of turbulence and large eddy simulation, our results are as accurate as baseline solvers with 8-10x finer resolution in each spatial dimension, resulting in 40-80x fold computational speedups. Our method remains stable during long simulations, and generalizes to forcing functions and Reynolds numbers outside of the flows where it is trained, in contrast to black box machine learning approaches. Our approach exemplifies how scientific computing can leverage machine learning and hardware accelerators to improve simulations without sacrificing accuracy or generalization.
Learning Memory Access Patterns
Mar 06, 2018



Abstract:The explosion in workload complexity and the recent slow-down in Moore's law scaling call for new approaches towards efficient computing. Researchers are now beginning to use recent advances in machine learning in software optimizations, augmenting or replacing traditional heuristics and data structures. However, the space of machine learning for computer hardware architecture is only lightly explored. In this paper, we demonstrate the potential of deep learning to address the von Neumann bottleneck of memory performance. We focus on the critical problem of learning memory access patterns, with the goal of constructing accurate and efficient memory prefetchers. We relate contemporary prefetching strategies to n-gram models in natural language processing, and show how recurrent neural networks can serve as a drop-in replacement. On a suite of challenging benchmark datasets, we find that neural networks consistently demonstrate superior performance in terms of precision and recall. This work represents the first step towards practical neural-network based prefetching, and opens a wide range of exciting directions for machine learning in computer architecture research.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge