FEABench: Evaluating Language Models on Multiphysics Reasoning Ability

Building precise simulations of the real world and invoking numerical solvers to answer quantitative problems is an essential requirement in engineering and science. We present FEABench, a benchmark to evaluate the ability of large language models (LLMs) and LLM agents to simulate and solve physics, mathematics and engineering problems using finite element analysis (FEA). We introduce a comprehensive evaluation scheme to investigate the ability of LLMs to solve these problems end-to-end by reasoning over natural language problem descriptions and operating COMSOL Multiphysics$^\circledR$, an FEA software, to compute the answers. We additionally design a language model agent equipped with the ability to interact with the software through its Application Programming Interface (API), examine its outputs and use tools to improve its solutions over multiple iterations. Our best performing strategy generates executable API calls 88% of the time. LLMs that can successfully interact with and operate FEA software to solve problems such as those in our benchmark would push the frontiers of automation in engineering. Acquiring this capability would augment LLMs' reasoning skills with the precision of numerical solvers and advance the development of autonomous systems that can tackle complex problems in the real world. The code is available at https://github.com/google/feabench

Neural General Circulation Models

General circulation models (GCMs) are the foundation of weather and climate prediction. GCMs are physics-based simulators which combine a numerical solver for large-scale dynamics with tuned representations for small-scale processes such as cloud formation. Recently, machine learning (ML) models trained on reanalysis data achieved comparable or better skill than GCMs for deterministic weather forecasting. However, these models have not demonstrated improved ensemble forecasts, or shown sufficient stability for long-term weather and climate simulations. Here we present the first GCM that combines a differentiable solver for atmospheric dynamics with ML components, and show that it can generate forecasts of deterministic weather, ensemble weather and climate on par with the best ML and physics-based methods. NeuralGCM is competitive with ML models for 1-10 day forecasts, and with the European Centre for Medium-Range Weather Forecasts ensemble prediction for 1-15 day forecasts. With prescribed sea surface temperature, NeuralGCM can accurately track climate metrics such as global mean temperature for multiple decades, and climate forecasts with 140 km resolution exhibit emergent phenomena such as realistic frequency and trajectories of tropical cyclones. For both weather and climate, our approach offers orders of magnitude computational savings over conventional GCMs. Our results show that end-to-end deep learning is compatible with tasks performed by conventional GCMs, and can enhance the large-scale physical simulations that are essential for understanding and predicting the Earth system.

Learning to correct spectral methods for simulating turbulent flows

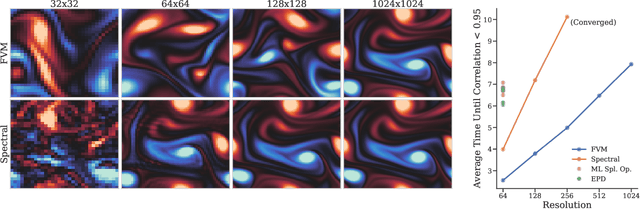
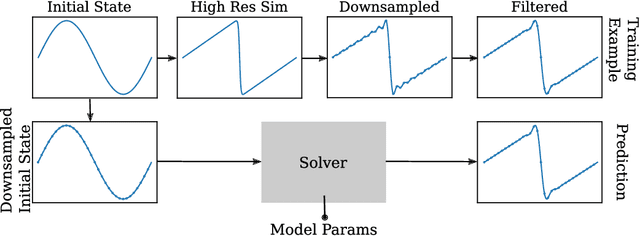
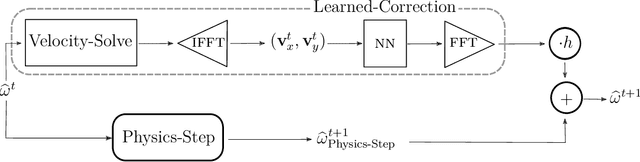
Despite their ubiquity throughout science and engineering, only a handful of partial differential equations (PDEs) have analytical, or closed-form solutions. This motivates a vast amount of classical work on numerical simulation of PDEs and more recently, a whirlwind of research into data-driven techniques leveraging machine learning (ML). A recent line of work indicates that a hybrid of classical numerical techniques with machine learning can offer significant improvements over either approach alone. In this work, we show that the choice of the numerical scheme is crucial when incorporating physics-based priors. We build upon Fourier-based spectral methods, which are considerably more efficient than other numerical schemes for simulating PDEs with smooth and periodic solutions. Specifically, we develop ML-augmented spectral solvers for three model PDEs of fluid dynamics, which improve upon the accuracy of standard spectral solvers at the same resolution. We also demonstrate a handful of key design principles for combining machine learning and numerical methods for solving PDEs.