Statistical Downscaling via High-Dimensional Distribution Matching with Generative Models

Statistical downscaling is a technique used in climate modeling to increase the resolution of climate simulations. High-resolution climate information is essential for various high-impact applications, including natural hazard risk assessment. However, simulating climate at high resolution is intractable. Thus, climate simulations are often conducted at a coarse scale and then downscaled to the desired resolution. Existing downscaling techniques are either simulation-based methods with high computational costs, or statistical approaches with limitations in accuracy or application specificity. We introduce Generative Bias Correction and Super-Resolution (GenBCSR), a two-stage probabilistic framework for statistical downscaling that overcomes the limitations of previous methods. GenBCSR employs two transformations to match high-dimensional distributions at different resolutions: (i) the first stage, bias correction, aligns the distributions at coarse scale, (ii) the second stage, statistical super-resolution, lifts the corrected coarse distribution by introducing fine-grained details. Each stage is instantiated by a state-of-the-art generative model, resulting in an efficient and effective computational pipeline for the well-studied distribution matching problem. By framing the downscaling problem as distribution matching, GenBCSR relaxes the constraints of supervised learning, which requires samples to be aligned. Despite not requiring such correspondence, we show that GenBCSR surpasses standard approaches in predictive accuracy of critical impact variables, particularly in predicting the tails (99% percentile) of composite indexes composed of interacting variables, achieving up to 4-5 folds of error reduction.

Dynamical-generative downscaling of climate model ensembles

Regional high-resolution climate projections are crucial for many applications, such as agriculture, hydrology, and natural hazard risk assessment. Dynamical downscaling, the state-of-the-art method to produce localized future climate information, involves running a regional climate model (RCM) driven by an Earth System Model (ESM), but it is too computationally expensive to apply to large climate projection ensembles. We propose a novel approach combining dynamical downscaling with generative artificial intelligence to reduce the cost and improve the uncertainty estimates of downscaled climate projections. In our framework, an RCM dynamically downscales ESM output to an intermediate resolution, followed by a generative diffusion model that further refines the resolution to the target scale. This approach leverages the generalizability of physics-based models and the sampling efficiency of diffusion models, enabling the downscaling of large multi-model ensembles. We evaluate our method against dynamically-downscaled climate projections from the CMIP6 ensemble. Our results demonstrate its ability to provide more accurate uncertainty bounds on future regional climate than alternatives such as dynamical downscaling of smaller ensembles, or traditional empirical statistical downscaling methods. We also show that dynamical-generative downscaling results in significantly lower errors than bias correction and spatial disaggregation (BCSD), and captures more accurately the spectra and multivariate correlations of meteorological fields. These characteristics make the dynamical-generative framework a flexible, accurate, and efficient way to downscale large ensembles of climate projections, currently out of reach for pure dynamical downscaling.

Generative AI for fast and accurate Statistical Computation of Fluids

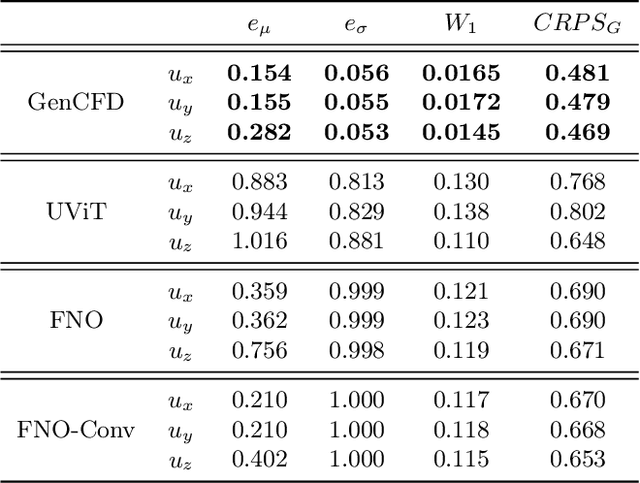
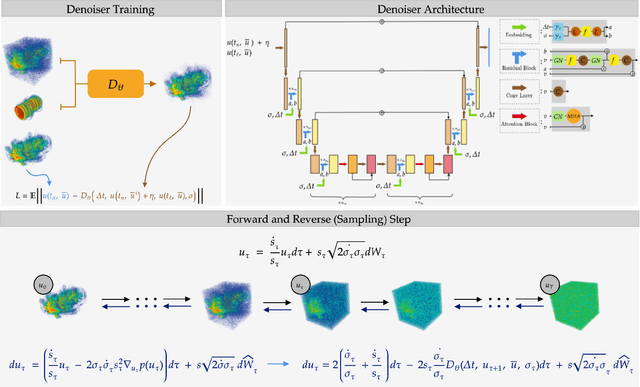
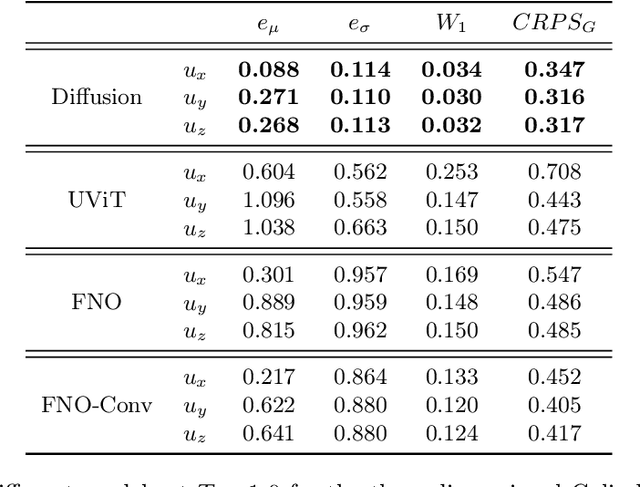
We present a generative AI algorithm for addressing the challenging task of fast, accurate and robust statistical computation of three-dimensional turbulent fluid flows. Our algorithm, termed as GenCFD, is based on a conditional score-based diffusion model. Through extensive numerical experimentation with both incompressible and compressible fluid flows, we demonstrate that GenCFD provides very accurate approximation of statistical quantities of interest such as mean, variance, point pdfs, higher-order moments, while also generating high quality realistic samples of turbulent fluid flows and ensuring excellent spectral resolution. In contrast, ensembles of operator learning baselines which are trained to minimize mean (absolute) square errors regress to the mean flow. We present rigorous theoretical results uncovering the surprising mechanisms through which diffusion models accurately generate fluid flows. These mechanisms are illustrated with solvable toy models that exhibit the relevant features of turbulent fluid flows while being amenable to explicit analytical formulas.

Rational-WENO: A lightweight, physically-consistent three-point weighted essentially non-oscillatory scheme

Conventional WENO3 methods are known to be highly dissipative at lower resolutions, introducing significant errors in the pre-asymptotic regime. In this paper, we employ a rational neural network to accurately estimate the local smoothness of the solution, dynamically adapting the stencil weights based on local solution features. As rational neural networks can represent fast transitions between smooth and sharp regimes, this approach achieves a granular reconstruction with significantly reduced dissipation, improving the accuracy of the simulation. The network is trained offline on a carefully chosen dataset of analytical functions, bypassing the need for differentiable solvers. We also propose a robust model selection criterion based on estimates of the interpolation's convergence order on a set of test functions, which correlates better with the model performance in downstream tasks. We demonstrate the effectiveness of our approach on several one-, two-, and three-dimensional fluid flow problems: our scheme generalizes across grid resolutions while handling smooth and discontinuous solutions. In most cases, our rational network-based scheme achieves higher accuracy than conventional WENO3 with the same stencil size, and in a few of them, it achieves accuracy comparable to WENO5, which uses a larger stencil.

Back-Projection Diffusion: Solving the Wideband Inverse Scattering Problem with Diffusion Models

We present \textit{Wideband back-projection diffusion}, an end-to-end probabilistic framework for approximating the posterior distribution induced by the inverse scattering map from wideband scattering data. This framework leverages conditional diffusion models coupled with the underlying physics of wave-propagation and symmetries in the problem, to produce highly accurate reconstructions. The framework introduces a factorization of the score function into a physics-based latent representation inspired by the filtered back-propagation formula and a conditional score function conditioned on this latent representation. These two steps are also constrained to obey symmetries in the formulation while being amenable to compression by imposing the rank structure found in the filtered back-projection formula. As a result, empirically, our framework is able to provide sharp reconstructions effortlessly, even recovering sub-Nyquist features in the multiple-scattering regime. It has low-sample and computational complexity, its number of parameters scales sub-linearly with the target resolution, and it has stable training dynamics.

A probabilistic framework for learning non-intrusive corrections to long-time climate simulations from short-time training data

Chaotic systems, such as turbulent flows, are ubiquitous in science and engineering. However, their study remains a challenge due to the large range scales, and the strong interaction with other, often not fully understood, physics. As a consequence, the spatiotemporal resolution required for accurate simulation of these systems is typically computationally infeasible, particularly for applications of long-term risk assessment, such as the quantification of extreme weather risk due to climate change. While data-driven modeling offers some promise of alleviating these obstacles, the scarcity of high-quality simulations results in limited available data to train such models, which is often compounded by the lack of stability for long-horizon simulations. As such, the computational, algorithmic, and data restrictions generally imply that the probability of rare extreme events is not accurately captured. In this work we present a general strategy for training neural network models to non-intrusively correct under-resolved long-time simulations of chaotic systems. The approach is based on training a post-processing correction operator on under-resolved simulations nudged towards a high-fidelity reference. This enables us to learn the dynamics of the underlying system directly, which allows us to use very little training data, even when the statistics thereof are far from converged. Additionally, through the use of probabilistic network architectures we are able to leverage the uncertainty due to the limited training data to further improve extrapolation capabilities. We apply our framework to severely under-resolved simulations of quasi-geostrophic flow and demonstrate its ability to accurately predict the anisotropic statistics over time horizons more than 30 times longer than the data seen in training.

DySLIM: Dynamics Stable Learning by Invariant Measure for Chaotic Systems

Learning dynamics from dissipative chaotic systems is notoriously difficult due to their inherent instability, as formalized by their positive Lyapunov exponents, which exponentially amplify errors in the learned dynamics. However, many of these systems exhibit ergodicity and an attractor: a compact and highly complex manifold, to which trajectories converge in finite-time, that supports an invariant measure, i.e., a probability distribution that is invariant under the action of the dynamics, which dictates the long-term statistical behavior of the system. In this work, we leverage this structure to propose a new framework that targets learning the invariant measure as well as the dynamics, in contrast with typical methods that only target the misfit between trajectories, which often leads to divergence as the trajectories' length increases. We use our framework to propose a tractable and sample efficient objective that can be used with any existing learning objectives. Our Dynamics Stable Learning by Invariant Measures (DySLIM) objective enables model training that achieves better point-wise tracking and long-term statistical accuracy relative to other learning objectives. By targeting the distribution with a scalable regularization term, we hope that this approach can be extended to more complex systems exhibiting slowly-variant distributions, such as weather and climate models.

User-defined Event Sampling and Uncertainty Quantification in Diffusion Models for Physical Dynamical Systems

Diffusion models are a class of probabilistic generative models that have been widely used as a prior for image processing tasks like text conditional generation and inpainting. We demonstrate that these models can be adapted to make predictions and provide uncertainty quantification for chaotic dynamical systems. In these applications, diffusion models can implicitly represent knowledge about outliers and extreme events; however, querying that knowledge through conditional sampling or measuring probabilities is surprisingly difficult. Existing methods for conditional sampling at inference time seek mainly to enforce the constraints, which is insufficient to match the statistics of the distribution or compute the probability of the chosen events. To achieve these ends, optimally one would use the conditional score function, but its computation is typically intractable. In this work, we develop a probabilistic approximation scheme for the conditional score function which provably converges to the true distribution as the noise level decreases. With this scheme we are able to sample conditionally on nonlinear userdefined events at inference time, and matches data statistics even when sampling from the tails of the distribution.

Neural Ideal Large Eddy Simulation: Modeling Turbulence with Neural Stochastic Differential Equations

We introduce a data-driven learning framework that assimilates two powerful ideas: ideal large eddy simulation (LES) from turbulence closure modeling and neural stochastic differential equations (SDE) for stochastic modeling. The ideal LES models the LES flow by treating each full-order trajectory as a random realization of the underlying dynamics, as such, the effect of small-scales is marginalized to obtain the deterministic evolution of the LES state. However, ideal LES is analytically intractable. In our work, we use a latent neural SDE to model the evolution of the stochastic process and an encoder-decoder pair for transforming between the latent space and the desired ideal flow field. This stands in sharp contrast to other types of neural parameterization of closure models where each trajectory is treated as a deterministic realization of the dynamics. We show the effectiveness of our approach (niLES - neural ideal LES) on a challenging chaotic dynamical system: Kolmogorov flow at a Reynolds number of 20,000. Compared to competing methods, our method can handle non-uniform geometries using unstructured meshes seamlessly. In particular, niLES leads to trajectories with more accurate statistics and enhances stability, particularly for long-horizon rollouts.

Debias Coarsely, Sample Conditionally: Statistical Downscaling through Optimal Transport and Probabilistic Diffusion Models

We introduce a two-stage probabilistic framework for statistical downscaling between unpaired data. Statistical downscaling seeks a probabilistic map to transform low-resolution data from a (possibly biased) coarse-grained numerical scheme to high-resolution data that is consistent with a high-fidelity scheme. Our framework tackles the problem by tandeming two transformations: a debiasing step that is performed by an optimal transport map, and an upsampling step that is achieved by a probabilistic diffusion model with \textit{a posteriori} conditional sampling. This approach characterizes a conditional distribution without the need for paired data, and faithfully recovers relevant physical statistics from biased samples. We demonstrate the utility of the proposed approach on one- and two-dimensional fluid flow problems, which are representative of the core difficulties present in numerical simulations of weather and climate. Our method produces realistic high-resolution outputs from low-resolution inputs, by upsampling resolutions of $8\times$ and $16\times$. Moreover, our procedure correctly matches the statistics of physical quantities, even when the low-frequency content of the inputs and outputs do not match, a crucial but difficult-to-satisfy assumption needed by current state-of-the-art alternatives.