A probabilistic framework for learning non-intrusive corrections to long-time climate simulations from short-time training data

Chaotic systems, such as turbulent flows, are ubiquitous in science and engineering. However, their study remains a challenge due to the large range scales, and the strong interaction with other, often not fully understood, physics. As a consequence, the spatiotemporal resolution required for accurate simulation of these systems is typically computationally infeasible, particularly for applications of long-term risk assessment, such as the quantification of extreme weather risk due to climate change. While data-driven modeling offers some promise of alleviating these obstacles, the scarcity of high-quality simulations results in limited available data to train such models, which is often compounded by the lack of stability for long-horizon simulations. As such, the computational, algorithmic, and data restrictions generally imply that the probability of rare extreme events is not accurately captured. In this work we present a general strategy for training neural network models to non-intrusively correct under-resolved long-time simulations of chaotic systems. The approach is based on training a post-processing correction operator on under-resolved simulations nudged towards a high-fidelity reference. This enables us to learn the dynamics of the underlying system directly, which allows us to use very little training data, even when the statistics thereof are far from converged. Additionally, through the use of probabilistic network architectures we are able to leverage the uncertainty due to the limited training data to further improve extrapolation capabilities. We apply our framework to severely under-resolved simulations of quasi-geostrophic flow and demonstrate its ability to accurately predict the anisotropic statistics over time horizons more than 30 times longer than the data seen in training.

A non-intrusive machine learning framework for debiasing long-time coarse resolution climate simulations and quantifying rare events statistics

Due to the rapidly changing climate, the frequency and severity of extreme weather is expected to increase over the coming decades. As fully-resolved climate simulations remain computationally intractable, policy makers must rely on coarse-models to quantify risk for extremes. However, coarse models suffer from inherent bias due to the ignored "sub-grid" scales. We propose a framework to non-intrusively debias coarse-resolution climate predictions using neural-network (NN) correction operators. Previous efforts have attempted to train such operators using loss functions that match statistics. However, this approach falls short with events that have longer return period than that of the training data, since the reference statistics have not converged. Here, the scope is to formulate a learning method that allows for correction of dynamics and quantification of extreme events with longer return period than the training data. The key obstacle is the chaotic nature of the underlying dynamics. To overcome this challenge, we introduce a dynamical systems approach where the correction operator is trained using reference data and a coarse model simulation nudged towards that reference. The method is demonstrated on debiasing an under-resolved quasi-geostrophic model and the Energy Exascale Earth System Model (E3SM). For the former, our method enables the quantification of events that have return period two orders longer than the training data. For the latter, when trained on 8 years of ERA5 data, our approach is able to correct the coarse E3SM output to closely reflect the 36-year ERA5 statistics for all prognostic variables and significantly reduce their spatial biases.

Output-weighted and relative entropy loss functions for deep learning precursors of extreme events

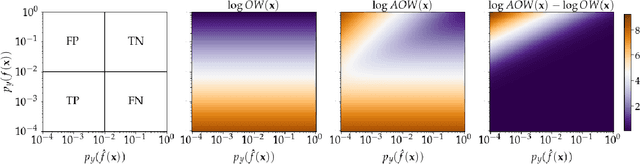
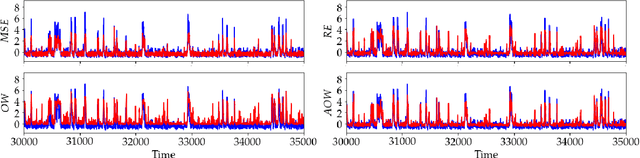
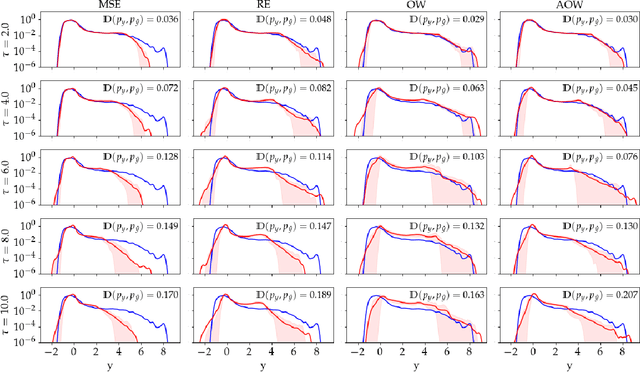
Many scientific and engineering problems require accurate models of dynamical systems with rare and extreme events. Such problems present a challenging task for data-driven modelling, with many naive machine learning methods failing to predict or accurately quantify such events. One cause for this difficulty is that systems with extreme events, by definition, yield imbalanced datasets and that standard loss functions easily ignore rare events. That is, metrics for goodness of fit used to train models are not designed to ensure accuracy on rare events. This work seeks to improve the performance of regression models for extreme events by considering loss functions designed to highlight outliers. We propose a novel loss function, the adjusted output weighted loss, and extend the applicability of relative entropy based loss functions to systems with low dimensional output. The proposed functions are tested using several cases of dynamical systems exhibiting extreme events and shown to significantly improve accuracy in predictions of extreme events.

Output-Weighted Sampling for Multi-Armed Bandits with Extreme Payoffs

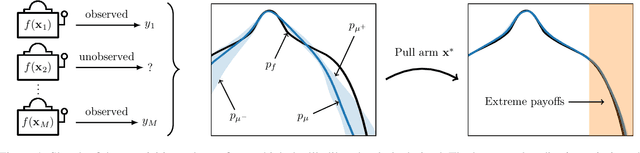
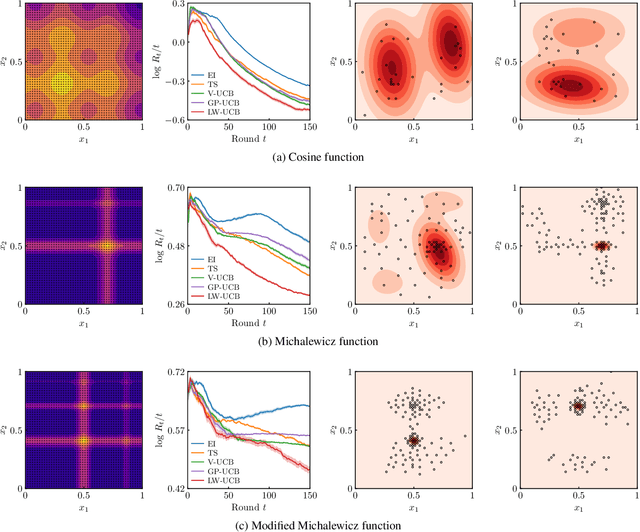
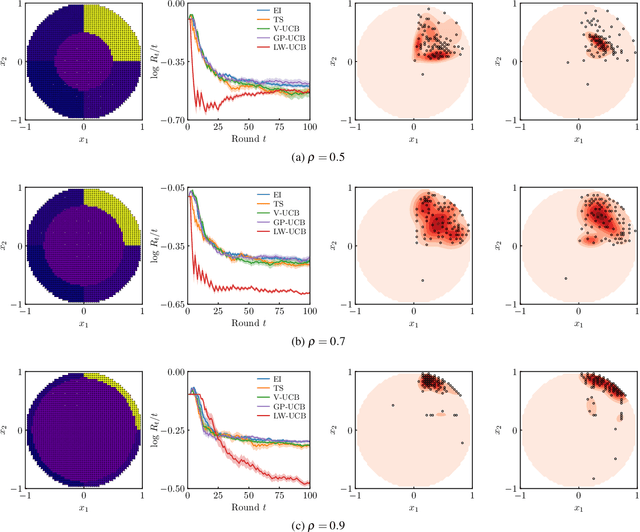
We present a new type of acquisition functions for online decision making in multi-armed and contextual bandit problems with extreme payoffs. Specifically, we model the payoff function as a Gaussian process and formulate a novel type of upper confidence bound (UCB) acquisition function that guides exploration towards the bandits that are deemed most relevant according to the variability of the observed rewards. This is achieved by computing a tractable likelihood ratio that quantifies the importance of the output relative to the inputs and essentially acts as an \textit{attention mechanism} that promotes exploration of extreme rewards. We demonstrate the benefits of the proposed methodology across several synthetic benchmarks, as well as a realistic example involving noisy sensor network data. Finally, we provide a JAX library for efficient bandit optimization using Gaussian processes.

Output-Weighted Importance Sampling for Bayesian Experimental Design and Uncertainty Quantification

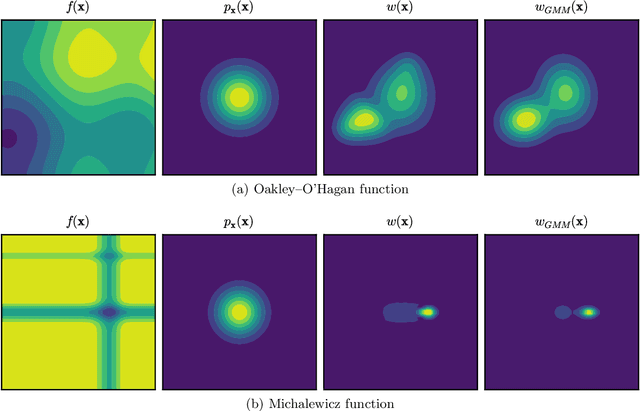
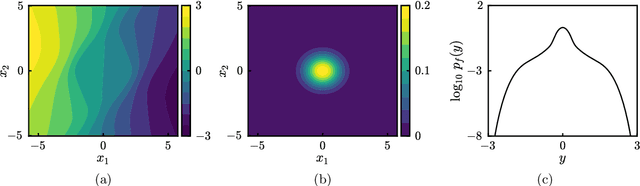
We introduce a class of acquisition functions for sample selection that leads to faster convergence in applications related to Bayesian experimental design and uncertainty quantification. The approach follows the paradigm of active learning, whereby existing samples of a black-box function are utilized to optimize the next most informative sample. The proposed method aims to take advantage of the fact that some input directions of the black-box function have a larger impact on the output than others, which is important especially for systems exhibiting rare and extreme events. The acquisition functions introduced in this work leverage the properties of the likelihood ratio, a quantity that acts as a probabilistic sampling weight and guides the active-learning algorithm towards regions of the input space that are deemed most relevant. We demonstrate superiority of the proposed approach in the uncertainty quantification of a hydrological system as well as the probabilistic quantification of rare events in dynamical systems and the identification of their precursors.

Informative Path Planning for Anomaly Detection in Environment Exploration and Monitoring

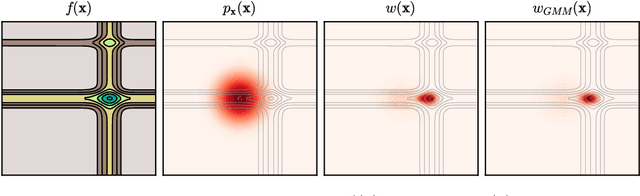
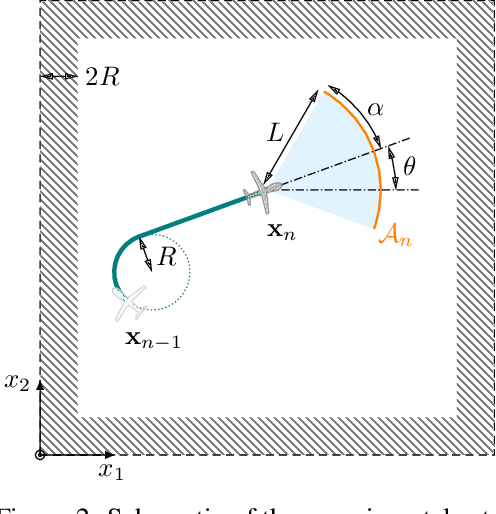
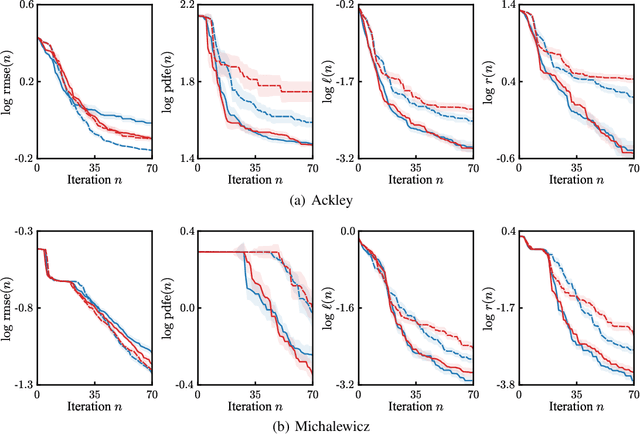
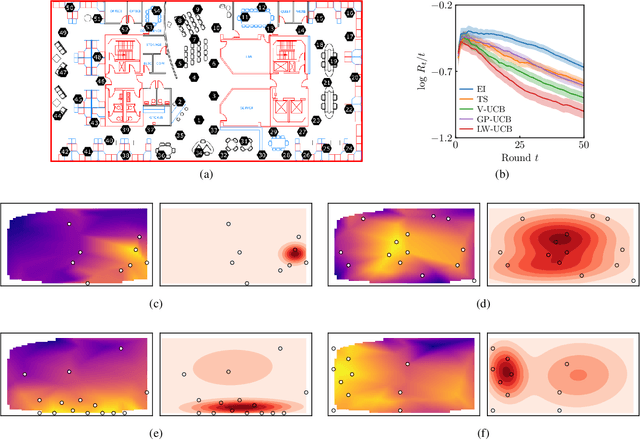
An unmanned autonomous vehicle (UAV) is sent on a mission to explore and reconstruct an unknown environment from a series of measurements collected by Bayesian optimization. The success of the mission is judged by the UAV's ability to faithfully reconstruct any anomalous feature present in the environment (e.g., extreme topographic depressions or abnormal chemical concentrations). We show that the criteria commonly used for determining which locations the UAV should visit are ill-suited for this task. We introduce a number of novel criteria that guide the UAV towards regions of strong anomalies by leveraging previously collected information in a mathematically elegant and computationally tractable manner. We demonstrate superiority of the proposed approach in several applications.

Bayesian Optimization with Output-Weighted Importance Sampling

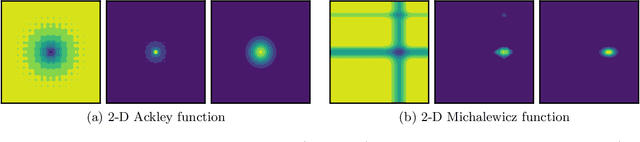
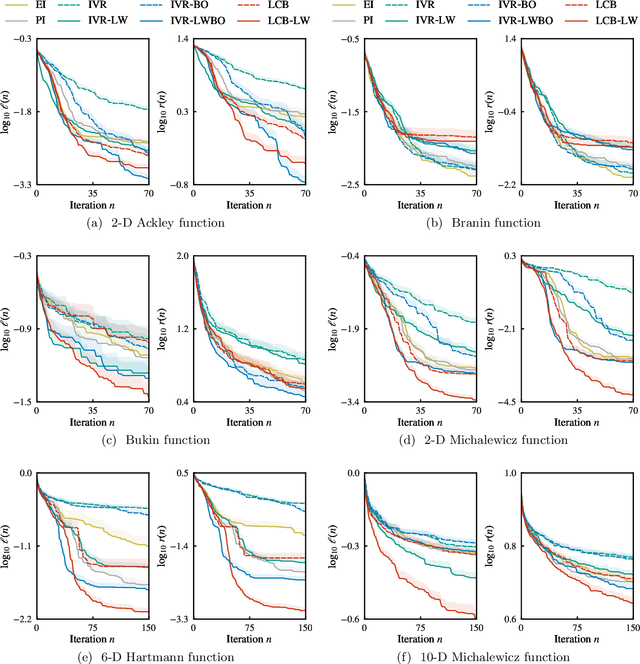
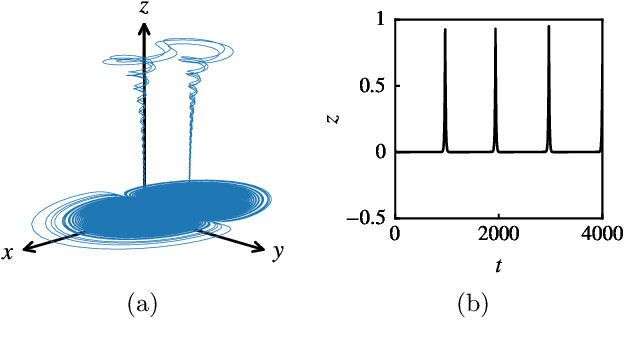
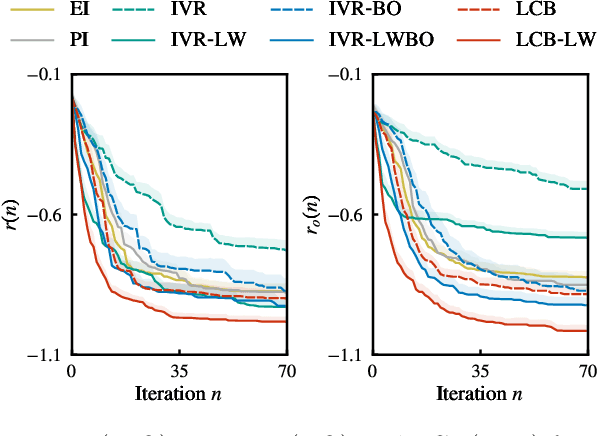
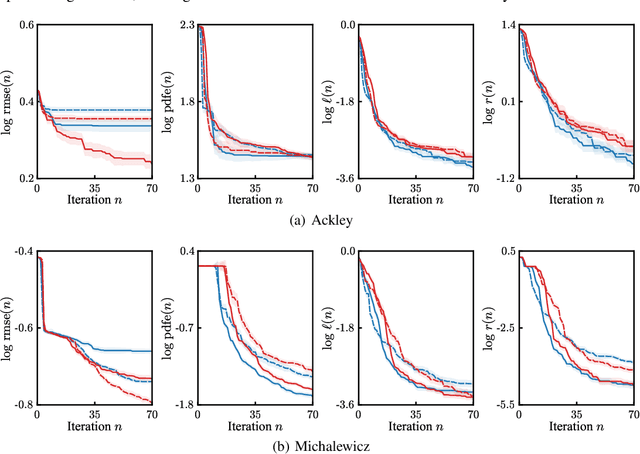
In Bayesian optimization, accounting for the importance of the output relative to the input is a crucial yet perilous exercise, as it can considerably improve the final result but often involves inaccurate and cumbersome entropy estimations. We approach the problem from a radically new perspective and, inspired by the theory of importance sampling and extreme events, advocate the use of the likelihood ratio to guide the search algorithm towards regions where the magnitude of the objective function is unusually large. The likelihood ratio acts as a sampling weight and can be approximated in a way that makes the approach tractable in high dimensions. The "likelihood-weighted" acquisition functions introduced in this work are found to outperform their unweighted counterparts substantially in a number of applications.