Output-Weighted Importance Sampling for Bayesian Experimental Design and Uncertainty Quantification

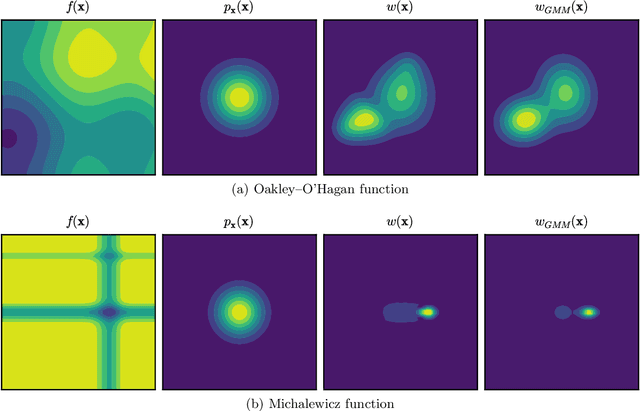
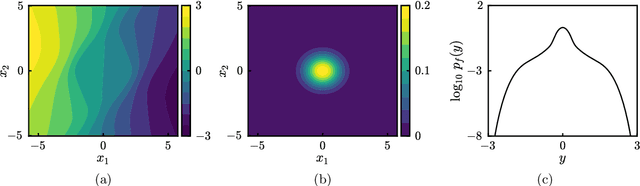
We introduce a class of acquisition functions for sample selection that leads to faster convergence in applications related to Bayesian experimental design and uncertainty quantification. The approach follows the paradigm of active learning, whereby existing samples of a black-box function are utilized to optimize the next most informative sample. The proposed method aims to take advantage of the fact that some input directions of the black-box function have a larger impact on the output than others, which is important especially for systems exhibiting rare and extreme events. The acquisition functions introduced in this work leverage the properties of the likelihood ratio, a quantity that acts as a probabilistic sampling weight and guides the active-learning algorithm towards regions of the input space that are deemed most relevant. We demonstrate superiority of the proposed approach in the uncertainty quantification of a hydrological system as well as the probabilistic quantification of rare events in dynamical systems and the identification of their precursors.