Antoine Blanchard
Continuous latent representations for modeling precipitation with deep learning
Dec 19, 2024Abstract:The sparse and spatio-temporally discontinuous nature of precipitation data presents significant challenges for simulation and statistical processing for bias correction and downscaling. These include incorrect representation of intermittency and extreme values (critical for hydrology applications), Gibbs phenomenon upon regridding, and lack of fine scales details. To address these challenges, a common approach is to transform the precipitation variable nonlinearly into one that is more malleable. In this work, we explore how deep learning can be used to generate a smooth, spatio-temporally continuous variable as a proxy for simulation of precipitation data. We develop a normally distributed field called pseudo-precipitation (PP) as an alternative for simulating precipitation. The practical applicability of this variable is investigated by applying it for downscaling precipitation from \(1\degree\) (\(\sim\) 100 km) to \(0.25\degree\) (\(\sim\) 25 km).
TAUDiff: Improving statistical downscaling for extreme weather events using generative diffusion models
Dec 18, 2024


Abstract:Deterministic regression-based downscaling models for climate variables often suffer from spectral bias, which can be mitigated by generative models like diffusion models. To enable efficient and reliable simulation of extreme weather events, it is crucial to achieve rapid turnaround, dynamical consistency, and accurate spatio-temporal spectral recovery. We propose an efficient correction diffusion model, TAUDiff, that combines a deterministic spatio-temporal model for mean field downscaling with a smaller generative diffusion model for recovering the fine-scale stochastic features. We demonstrate the efficacy of this approach on downscaling atmospheric wind velocity fields obtained from coarse GCM simulations. Our approach can not only ensure quicker simulation of extreme events but also reduce overall carbon footprint due to low inference times.
Output-Weighted Sampling for Multi-Armed Bandits with Extreme Payoffs
Feb 19, 2021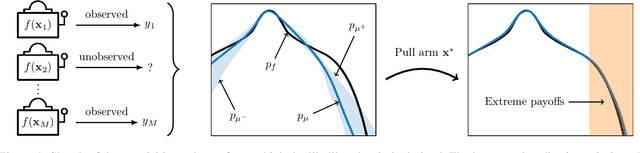
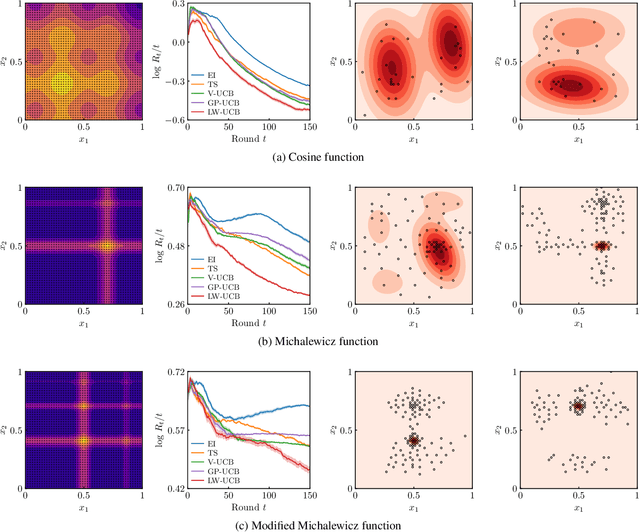
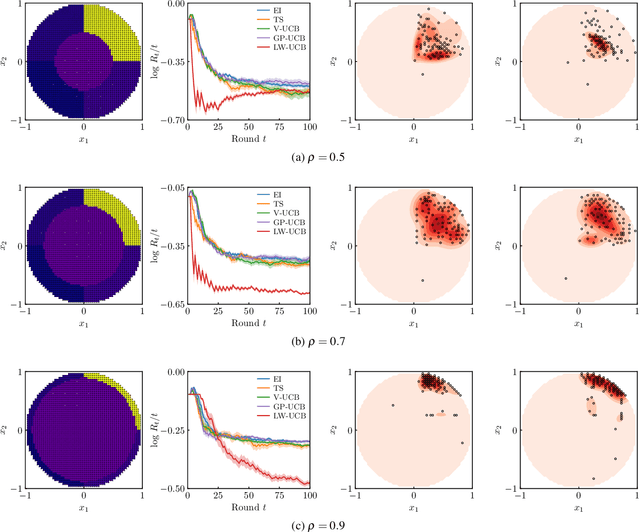
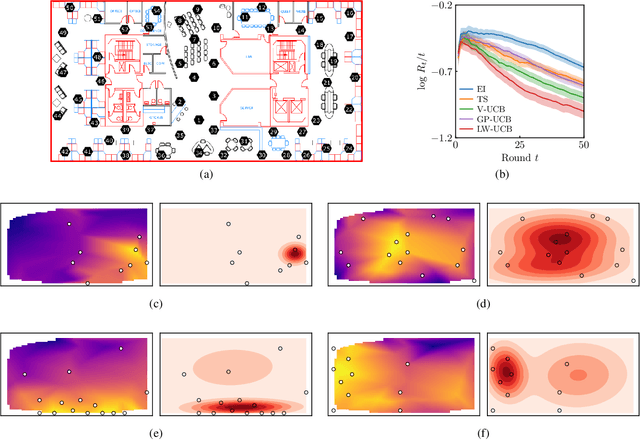
Abstract:We present a new type of acquisition functions for online decision making in multi-armed and contextual bandit problems with extreme payoffs. Specifically, we model the payoff function as a Gaussian process and formulate a novel type of upper confidence bound (UCB) acquisition function that guides exploration towards the bandits that are deemed most relevant according to the variability of the observed rewards. This is achieved by computing a tractable likelihood ratio that quantifies the importance of the output relative to the inputs and essentially acts as an \textit{attention mechanism} that promotes exploration of extreme rewards. We demonstrate the benefits of the proposed methodology across several synthetic benchmarks, as well as a realistic example involving noisy sensor network data. Finally, we provide a JAX library for efficient bandit optimization using Gaussian processes.
Output-Weighted Importance Sampling for Bayesian Experimental Design and Uncertainty Quantification
Jun 22, 2020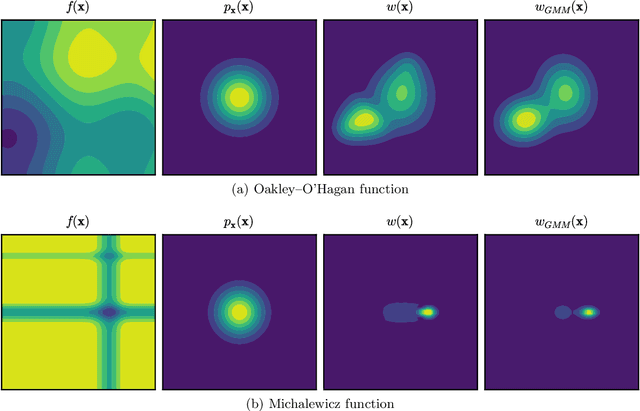
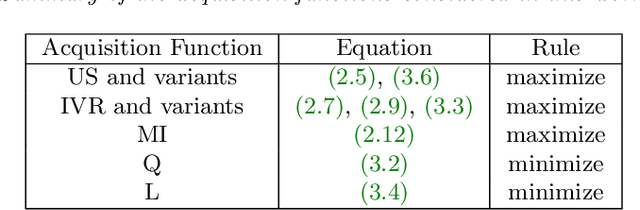
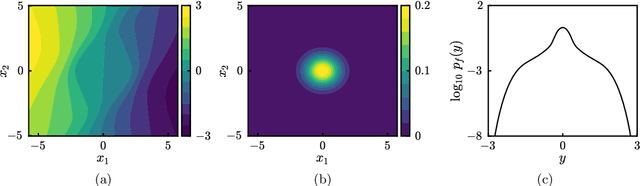

Abstract:We introduce a class of acquisition functions for sample selection that leads to faster convergence in applications related to Bayesian experimental design and uncertainty quantification. The approach follows the paradigm of active learning, whereby existing samples of a black-box function are utilized to optimize the next most informative sample. The proposed method aims to take advantage of the fact that some input directions of the black-box function have a larger impact on the output than others, which is important especially for systems exhibiting rare and extreme events. The acquisition functions introduced in this work leverage the properties of the likelihood ratio, a quantity that acts as a probabilistic sampling weight and guides the active-learning algorithm towards regions of the input space that are deemed most relevant. We demonstrate superiority of the proposed approach in the uncertainty quantification of a hydrological system as well as the probabilistic quantification of rare events in dynamical systems and the identification of their precursors.
Informative Path Planning for Anomaly Detection in Environment Exploration and Monitoring
May 21, 2020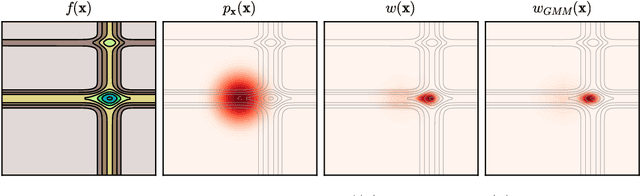
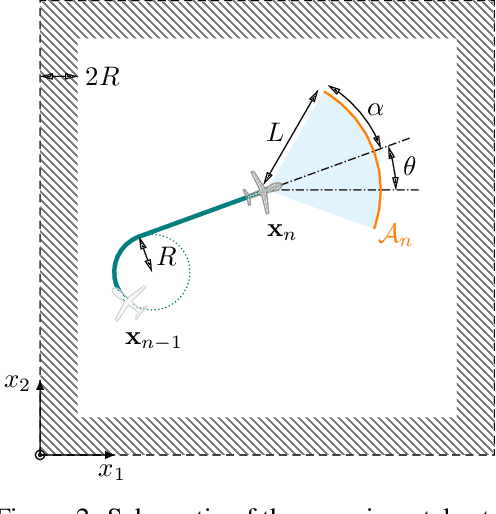
Abstract:An unmanned autonomous vehicle (UAV) is sent on a mission to explore and reconstruct an unknown environment from a series of measurements collected by Bayesian optimization. The success of the mission is judged by the UAV's ability to faithfully reconstruct any anomalous feature present in the environment (e.g., extreme topographic depressions or abnormal chemical concentrations). We show that the criteria commonly used for determining which locations the UAV should visit are ill-suited for this task. We introduce a number of novel criteria that guide the UAV towards regions of strong anomalies by leveraging previously collected information in a mathematically elegant and computationally tractable manner. We demonstrate superiority of the proposed approach in several applications.
Bayesian Optimization with Output-Weighted Importance Sampling
Apr 22, 2020
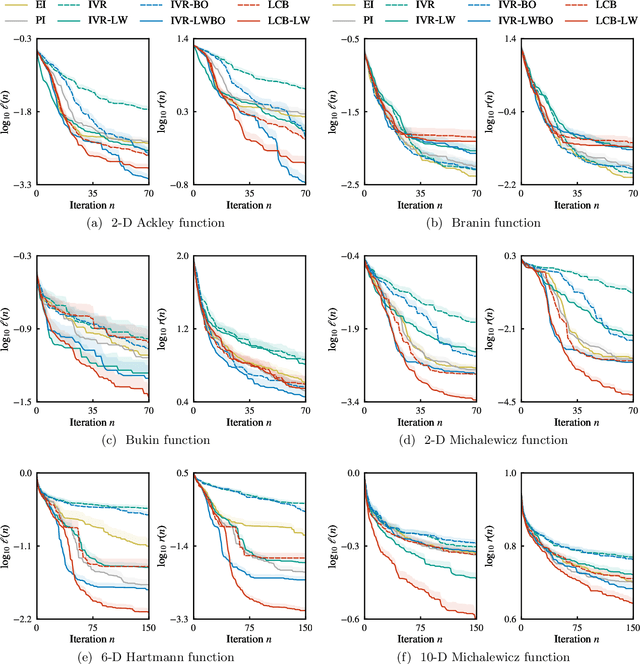
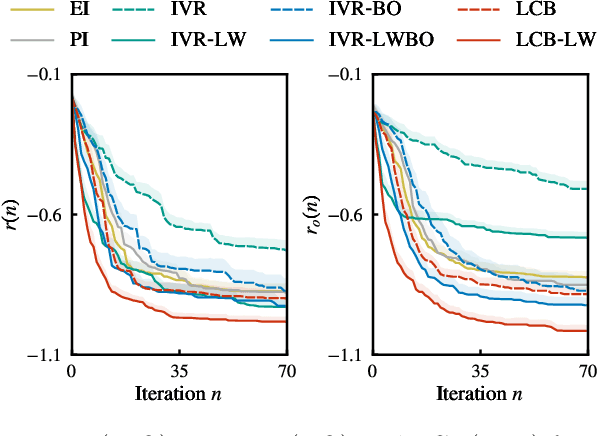
Abstract:In Bayesian optimization, accounting for the importance of the output relative to the input is a crucial yet perilous exercise, as it can considerably improve the final result but often involves inaccurate and cumbersome entropy estimations. We approach the problem from a radically new perspective and, inspired by the theory of importance sampling and extreme events, advocate the use of the likelihood ratio to guide the search algorithm towards regions where the magnitude of the objective function is unusually large. The likelihood ratio acts as a sampling weight and can be approximated in a way that makes the approach tractable in high dimensions. The "likelihood-weighted" acquisition functions introduced in this work are found to outperform their unweighted counterparts substantially in a number of applications.
Machine Learning the Tangent Space of Dynamical Instabilities from Data
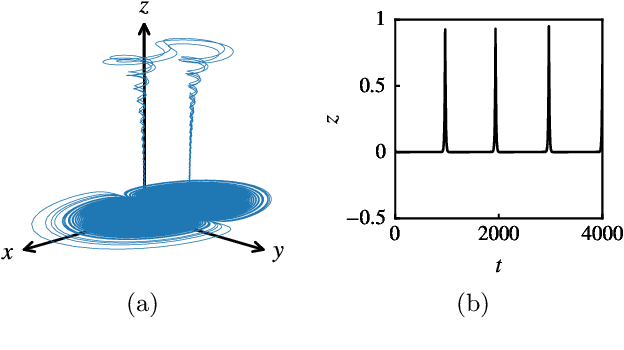
Jul 24, 2019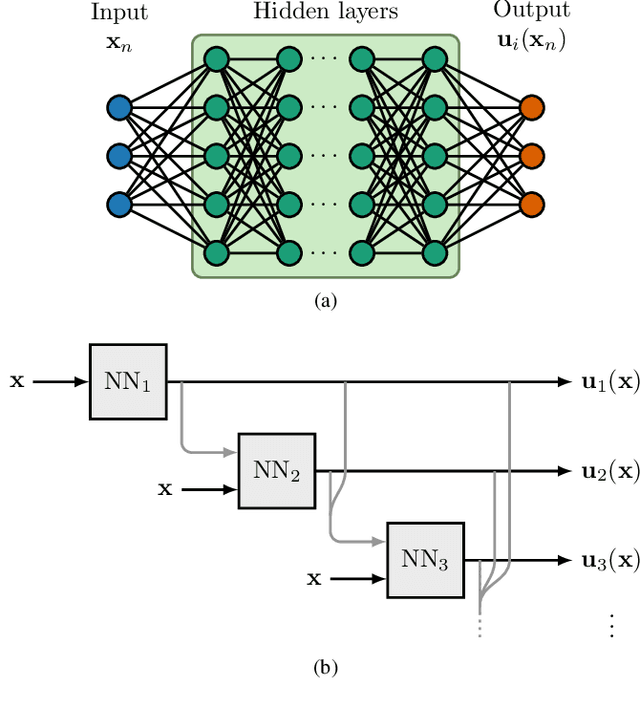
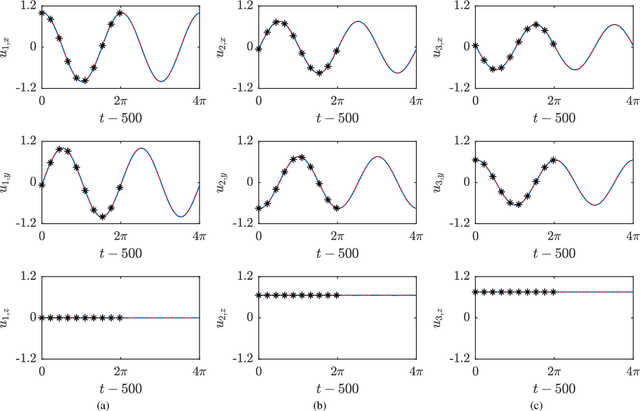
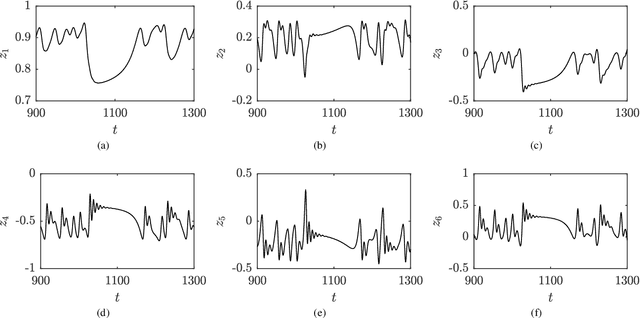
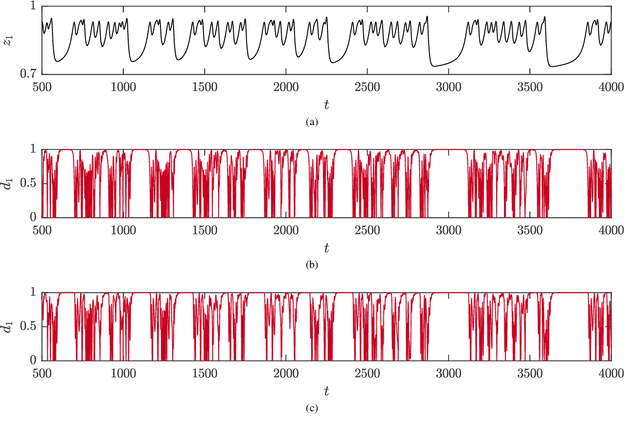
Abstract:For a large class of dynamical systems, the optimally time-dependent (OTD) modes, a set of deformable orthonormal tangent vectors that track directions of instabilities along any trajectory, are known to depend "pointwise" on the state of the system on the attractor, and not on the history of the trajectory. We leverage the power of neural networks to learn this "pointwise" mapping from phase space to OTD space directly from data. The result of the learning process is a cartography of directions associated with strongest instabilities in phase space. Implications for data-driven prediction and control of dynamical instabilities are discussed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge