Bayesian Optimization with Output-Weighted Importance Sampling

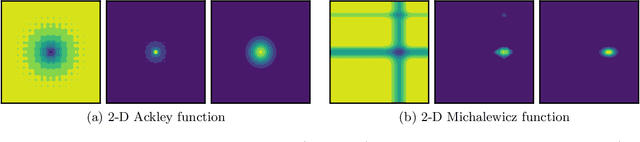
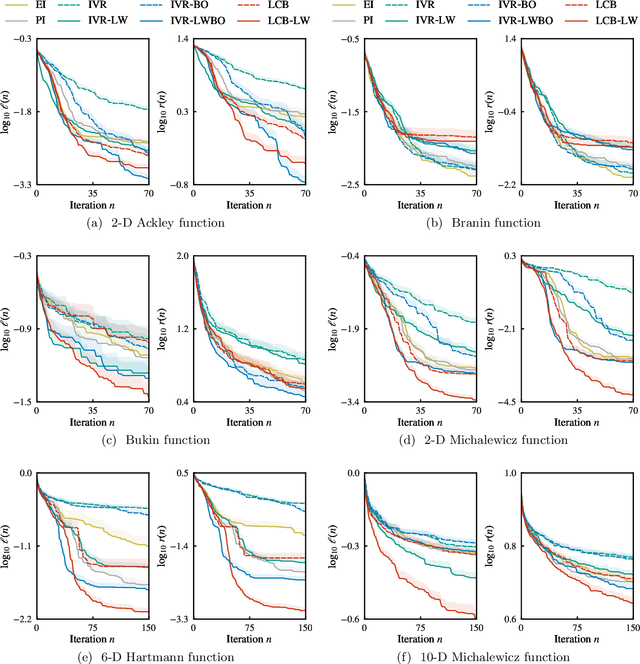
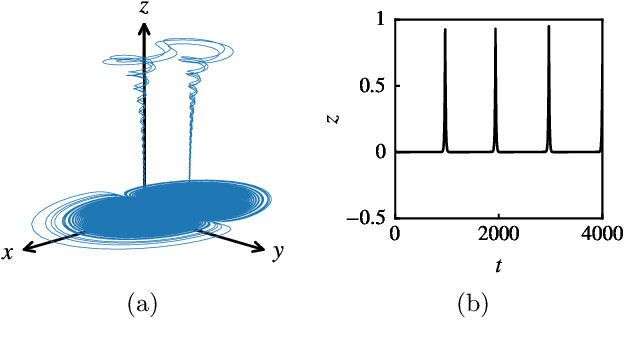
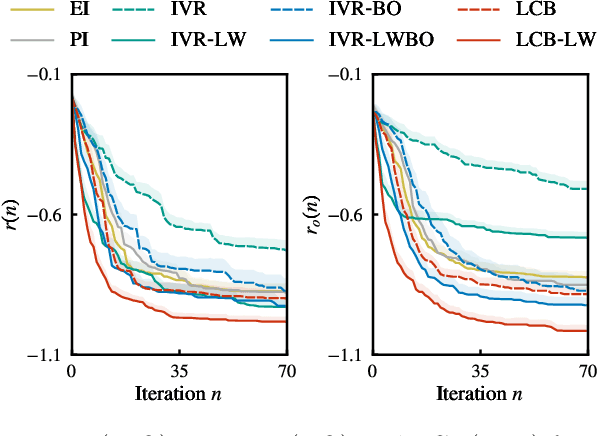
In Bayesian optimization, accounting for the importance of the output relative to the input is a crucial yet perilous exercise, as it can considerably improve the final result but often involves inaccurate and cumbersome entropy estimations. We approach the problem from a radically new perspective and, inspired by the theory of importance sampling and extreme events, advocate the use of the likelihood ratio to guide the search algorithm towards regions where the magnitude of the objective function is unusually large. The likelihood ratio acts as a sampling weight and can be approximated in a way that makes the approach tractable in high dimensions. The "likelihood-weighted" acquisition functions introduced in this work are found to outperform their unweighted counterparts substantially in a number of applications.