Output-Weighted Sampling for Multi-Armed Bandits with Extreme Payoffs
Paper and Code
Feb 19, 2021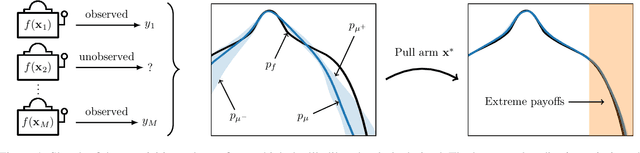
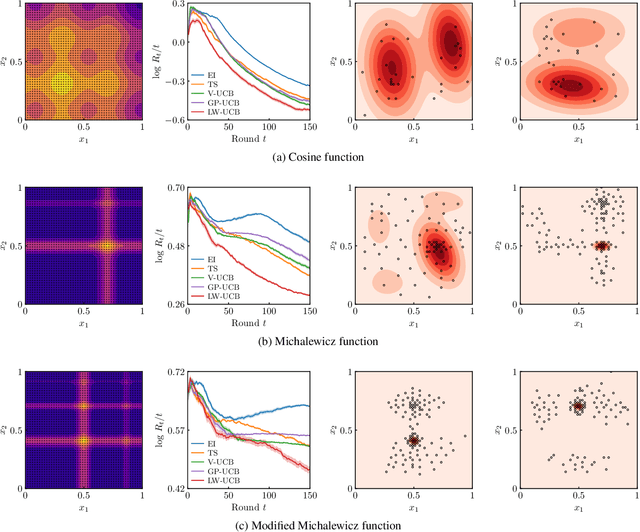
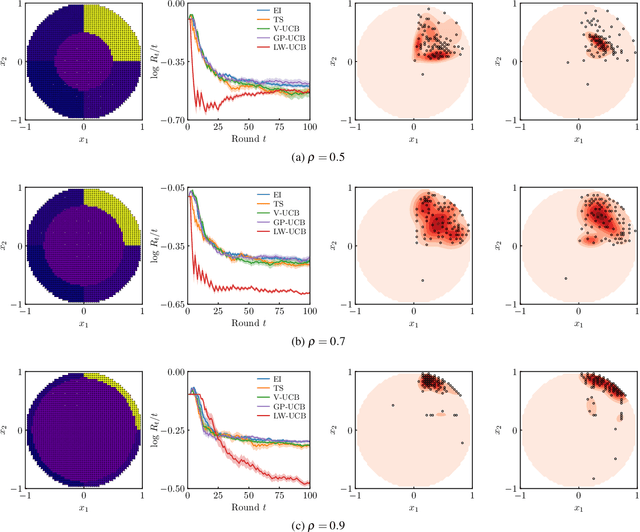
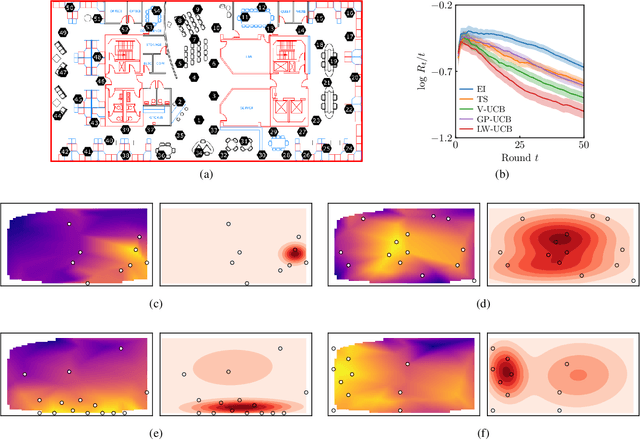
We present a new type of acquisition functions for online decision making in multi-armed and contextual bandit problems with extreme payoffs. Specifically, we model the payoff function as a Gaussian process and formulate a novel type of upper confidence bound (UCB) acquisition function that guides exploration towards the bandits that are deemed most relevant according to the variability of the observed rewards. This is achieved by computing a tractable likelihood ratio that quantifies the importance of the output relative to the inputs and essentially acts as an \textit{attention mechanism} that promotes exploration of extreme rewards. We demonstrate the benefits of the proposed methodology across several synthetic benchmarks, as well as a realistic example involving noisy sensor network data. Finally, we provide a JAX library for efficient bandit optimization using Gaussian processes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge