Active search for Bifurcations

Bifurcations mark qualitative changes of long-term behavior in dynamical systems and can often signal sudden ("hard") transitions or catastrophic events (divergences). Accurately locating them is critical not just for deeper understanding of observed dynamic behavior, but also for designing efficient interventions. When the dynamical system at hand is complex, possibly noisy, and expensive to sample, standard (e.g. continuation based) numerical methods may become impractical. We propose an active learning framework, where Bayesian Optimization is leveraged to discover saddle-node or Hopf bifurcations, from a judiciously chosen small number of vector field observations. Such an approach becomes especially attractive in systems whose state x parameter space exploration is resource-limited. It also naturally provides a framework for uncertainty quantification (aleatoric and epistemic), useful in systems with inherent stochasticity.

Multifidelity digital twin for real-time monitoring of structural dynamics in aquaculture net cages

As the global population grows and climate change intensifies, sustainable food production is critical. Marine aquaculture offers a viable solution, providing a sustainable protein source. However, the industry's expansion requires novel technologies for remote management and autonomous operations. Digital twin technology can advance the aquaculture industry, but its adoption has been limited. Fish net cages, which are flexible floating structures, are critical yet vulnerable components of aquaculture farms. Exposed to harsh and dynamic marine environments, the cages experience significant loads and risk damage, leading to fish escapes, environmental impacts, and financial losses. We propose a multifidelity surrogate modeling framework for integration into a digital twin for real-time monitoring of aquaculture net cage structural dynamics under stochastic marine conditions. Central to this framework is the nonlinear autoregressive Gaussian process method, which learns complex, nonlinear cross-correlations between models of varying fidelity. It combines low-fidelity simulation data with a small set of high-fidelity field sensor measurements, which offer the real dynamics but are costly and spatially sparse. Validated at the SINTEF ACE fish farm in Norway, our digital twin receives online metocean data and accurately predicts net cage displacements and mooring line loads, aligning closely with field measurements. The proposed framework is beneficial where application-specific data are scarce, offering rapid predictions and real-time system representation. The developed digital twin prevents potential damages by assessing structural integrity and facilitates remote operations with unmanned underwater vehicles. Our work also compares GP and GCNs for predicting net cage deformation, highlighting the latter's effectiveness in complex structural applications.

Multifidelity surrogate modeling, NARGP, digital twin, aquaculture net cage, real-time monitoring, graph convolutional networks

As the global population grows and climate change intensifies, sustainable food production is critical. Marine aquaculture offers a viable solution, providing a sustainable protein source. However, the industry's expansion requires novel technologies for remote management and autonomous operations. Digital twin technology can advance the aquaculture industry, but its adoption has been limited. Fish net cages, which are flexible floating structures, are critical yet vulnerable components of aquaculture farms. Exposed to harsh and dynamic marine environments, the cages experience significant loads and risk damage, leading to fish escapes, environmental impacts, and financial losses. We propose a multifidelity surrogate modeling framework for integration into a digital twin for real-time monitoring of aquaculture net cage structural dynamics under stochastic marine conditions. Central to this framework is the nonlinear autoregressive Gaussian process method, which learns complex, nonlinear cross-correlations between models of varying fidelity. It combines low-fidelity simulation data with a small set of high-fidelity field sensor measurements, which offer the real dynamics but are costly and spatially sparse. Validated at the SINTEF ACE fish farm in Norway, our digital twin receives online metocean data and accurately predicts net cage displacements and mooring line loads, aligning closely with field measurements. The proposed framework is beneficial where application-specific data are scarce, offering rapid predictions and real-time system representation. The developed digital twin prevents potential damages by assessing structural integrity and facilitates remote operations with unmanned underwater vehicles. Our work also compares GP and GCNs for predicting net cage deformation, highlighting the latter's effectiveness in complex structural applications.

Evaluation of machine learning architectures on the quantification of epistemic and aleatoric uncertainties in complex dynamical systems

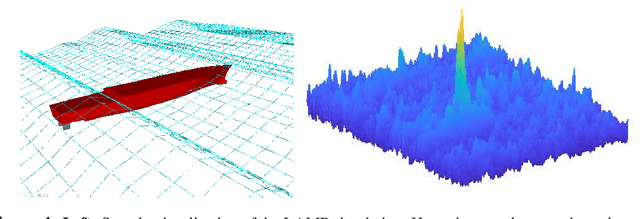
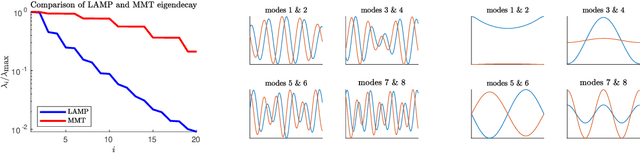
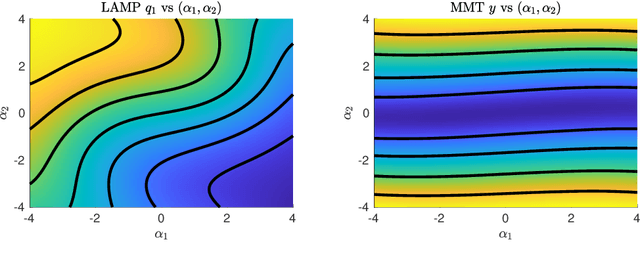
Machine learning methods for the construction of data-driven reduced order model models are used in an increasing variety of engineering domains, especially as a supplement to expensive computational fluid dynamics for design problems. An important check on the reliability of surrogate models is Uncertainty Quantification (UQ), a self assessed estimate of the model error. Accurate UQ allows for cost savings by reducing both the required size of training data sets and the required safety factors, while poor UQ prevents users from confidently relying on model predictions. We examine several machine learning techniques, including both Gaussian processes and a family UQ-augmented neural networks: Ensemble neural networks (ENN), Bayesian neural networks (BNN), Dropout neural networks (D-NN), and Gaussian neural networks (G-NN). We evaluate UQ accuracy (distinct from model accuracy) using two metrics: the distribution of normalized residuals on validation data, and the distribution of estimated uncertainties. We apply these metrics to two model data sets, representative of complex dynamical systems: an ocean engineering problem in which a ship traverses irregular wave episodes, and a dispersive wave turbulence system with extreme events, the Majda-McLaughlin-Tabak model. We present conclusions concerning model architecture and hyperparameter tuning.

Active Learning for Optimal Intervention Design in Causal Models

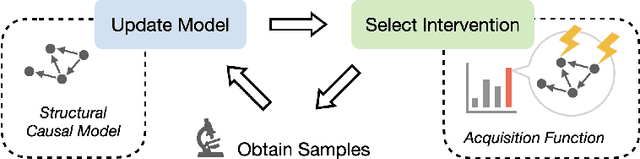
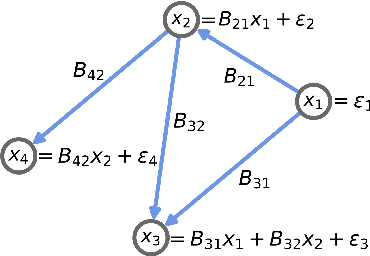
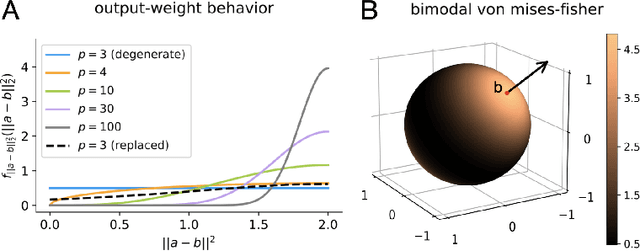
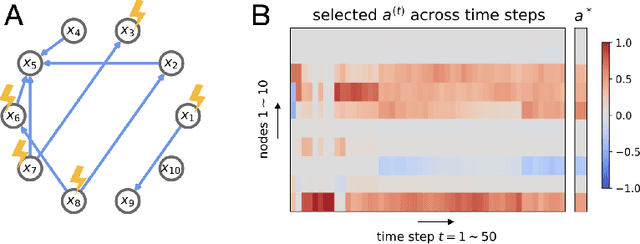
An important problem across disciplines is the discovery of interventions that produce a desired outcome. When the space of possible interventions is large, making an exhaustive search infeasible, experimental design strategies are needed. In this context, encoding the causal relationships between the variables, and thus the effect of interventions on the system, is critical in order to identify desirable interventions efficiently. We develop an iterative causal method to identify optimal interventions, as measured by the discrepancy between the post-interventional mean of the distribution and a desired target mean. We formulate an active learning strategy that uses the samples obtained so far from different interventions to update the belief about the underlying causal model, as well as to identify samples that are most informative about optimal interventions and thus should be acquired in the next batch. The approach employs a Bayesian update for the causal model and prioritizes interventions using a carefully designed, causally informed acquisition function. This acquisition function is evaluated in closed form, allowing for efficient optimization. The resulting algorithms are theoretically grounded with information-theoretic bounds and provable consistency results. We illustrate the method on both synthetic data and real-world biological data, namely gene expression data from Perturb-CITE-seq experiments, to identify optimal perturbations that induce a specific cell state transition; the proposed causal approach is observed to achieve better sample efficiency compared to several baselines. In both cases we observe that the causally informed acquisition function notably outperforms existing criteria allowing for optimal intervention design with significantly less experiments.

Information FOMO: The unhealthy fear of missing out on information. A method for removing misleading data for healthier models

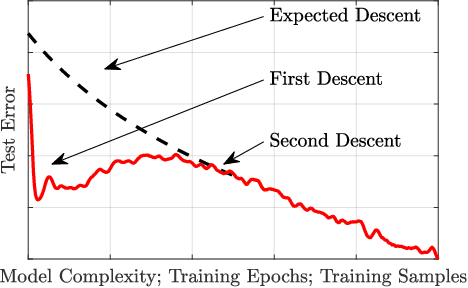
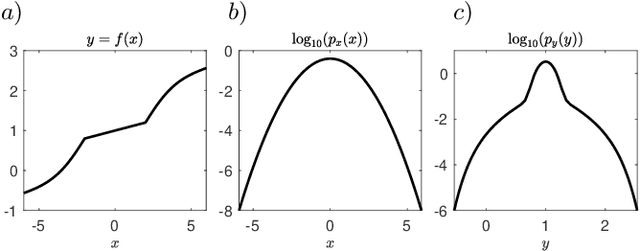
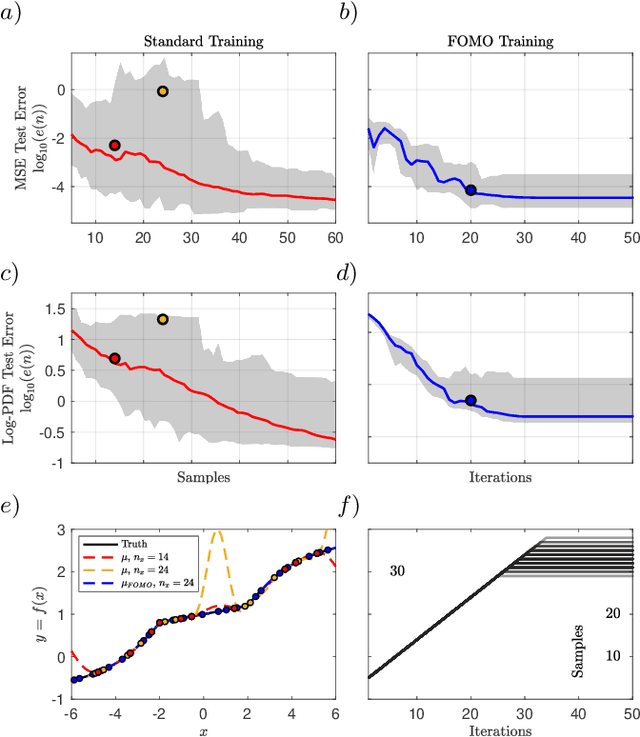
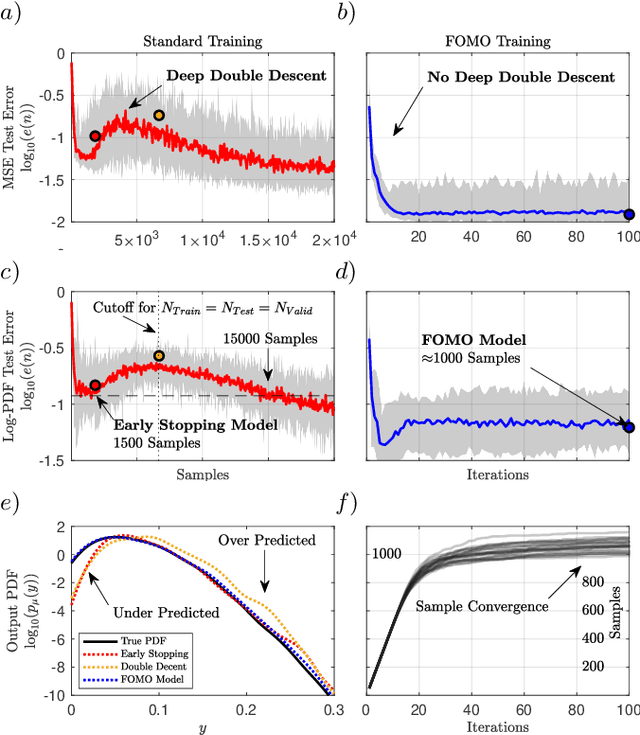
Not all data are equal. Misleading or unnecessary data can critically hinder the accuracy of Machine Learning (ML) models. When data is plentiful, misleading effects can be overcome, but in many real-world applications data is sparse and expensive to acquire. We present a method that substantially reduces the data size necessary to accurately train ML models, potentially opening the door for many new, limited-data applications in ML. Our method extracts the most informative data, while ignoring and omitting data that misleads the ML model to inferior generalization properties. Specifically, the method eliminates the phenomena of "double descent", where more data leads to worse performance. This approach brings several key features to the ML community. Notably, the method naturally converges and removes the traditional need to divide the dataset into training, testing, and validation data. Instead, the selection metric inherently assesses testing error. This ensures that key information is never wasted in testing or validation.

Discovering and forecasting extreme events via active learning in neural operators

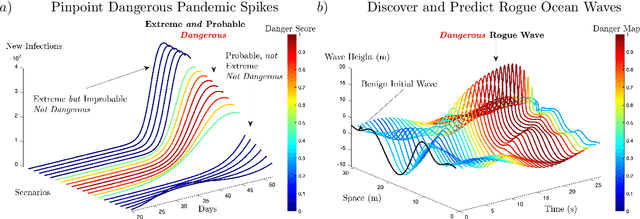
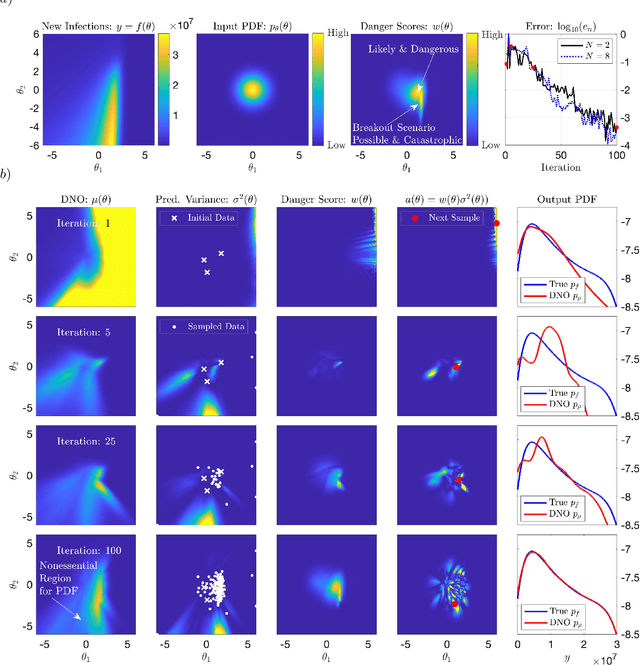
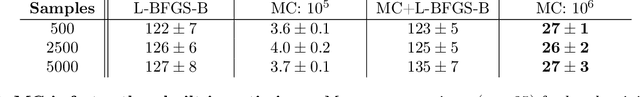
Extreme events in society and nature, such as pandemic spikes or rogue waves, can have catastrophic consequences. Characterizing extremes is difficult as they occur rarely, arise from seemingly benign conditions, and belong to complex and often unknown infinite-dimensional systems. Such challenges render attempts at characterizing them as moot. We address each of these difficulties by combining novel training schemes in Bayesian experimental design (BED) with an ensemble of deep neural operators (DNOs). This model-agnostic framework pairs a BED scheme that actively selects data for quantifying extreme events with an ensemble of DNOs that approximate infinite-dimensional nonlinear operators. We find that not only does this framework clearly beat Gaussian processes (GPs) but that 1) shallow ensembles of just two members perform best; 2) extremes are uncovered regardless of the state of initial data (i.e. with or without extremes); 3) our method eliminates "double-descent" phenomena; 4) the use of batches of suboptimal acquisition points compared to step-by-step global optima does not hinder BED performance; and 5) Monte Carlo acquisition outperforms standard minimizers in high-dimensions. Together these conclusions form the foundation of an AI-assisted experimental infrastructure that can efficiently infer and pinpoint critical situations across many domains, from physical to societal systems.

Structure and Distribution Metric for Quantifying the Quality of Uncertainty: Assessing Gaussian Processes, Deep Neural Nets, and Deep Neural Operators for Regression

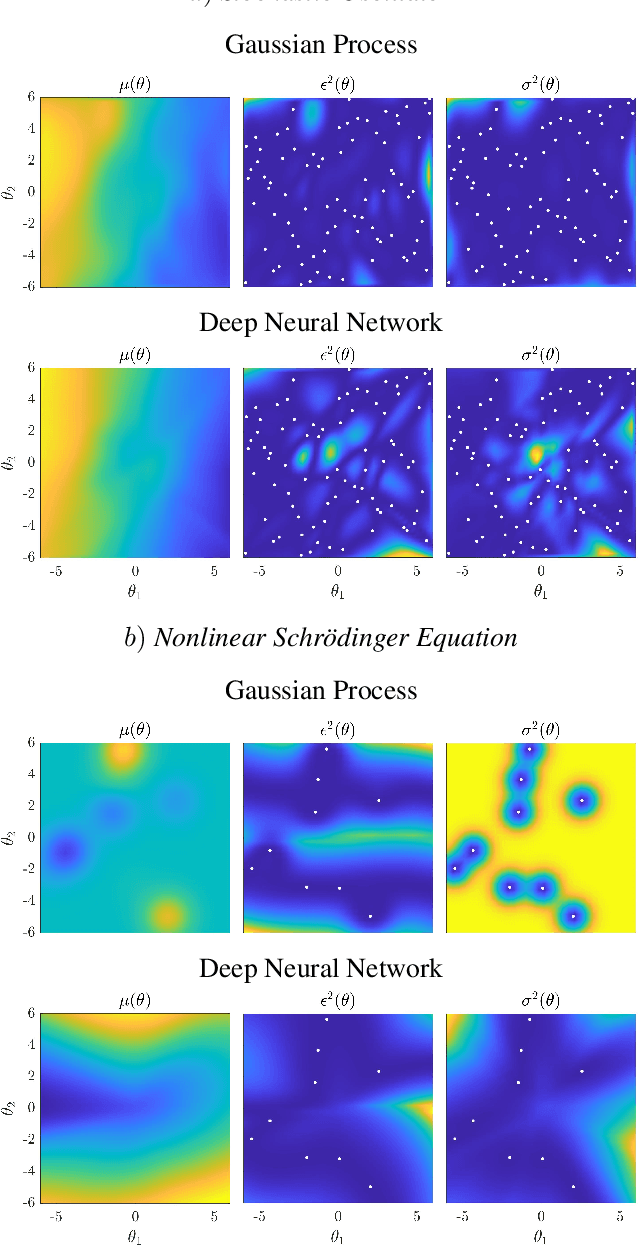
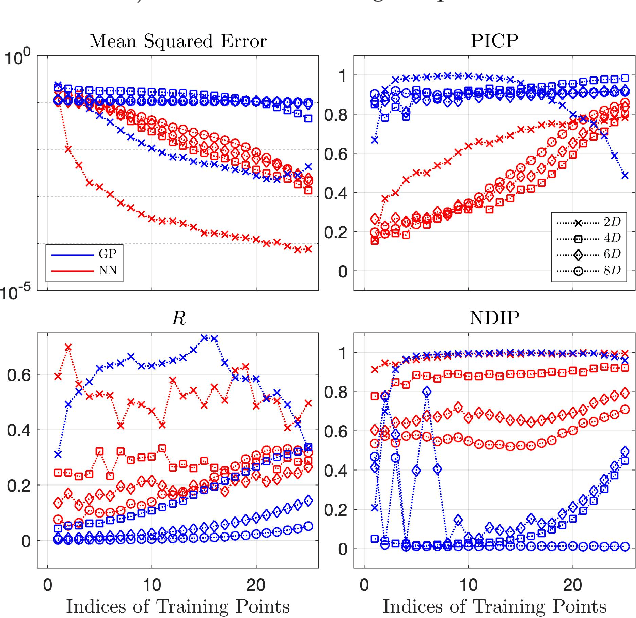
We propose two bounded comparison metrics that may be implemented to arbitrary dimensions in regression tasks. One quantifies the structure of uncertainty and the other quantifies the distribution of uncertainty. The structure metric assesses the similarity in shape and location of uncertainty with the true error, while the distribution metric quantifies the supported magnitudes between the two. We apply these metrics to Gaussian Processes (GPs), Ensemble Deep Neural Nets (DNNs), and Ensemble Deep Neural Operators (DNOs) on high-dimensional and nonlinear test cases. We find that comparing a model's uncertainty estimates with the model's squared error provides a compelling ground truth assessment. We also observe that both DNNs and DNOs, especially when compared to GPs, provide encouraging metric values in high dimensions with either sparse or plentiful data.

Sparse Methods for Automatic Relevance Determination

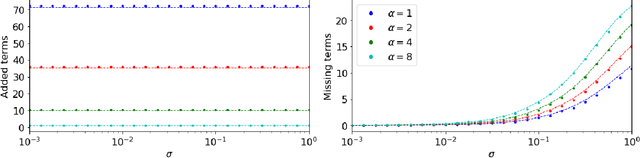
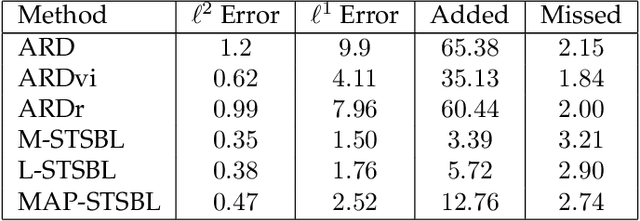
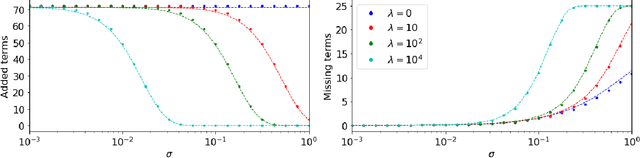
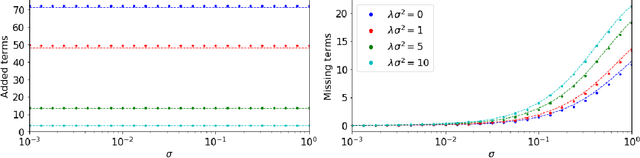
This work considers methods for imposing sparsity in Bayesian regression with applications in nonlinear system identification. We first review automatic relevance determination (ARD) and analytically demonstrate the need to additional regularization or thresholding to achieve sparse models. We then discuss two classes of methods, regularization based and thresholding based, which build on ARD to learn parsimonious solutions to linear problems. In the case of orthogonal covariates, we analytically demonstrate favorable performance with regards to learning a small set of active terms in a linear system with a sparse solution. Several example problems are presented to compare the set of proposed methods in terms of advantages and limitations to ARD in bases with hundreds of elements. The aim of this paper is to analyze and understand the assumptions that lead to several algorithms and to provide theoretical and empirical results so that the reader may gain insight and make more informed choices regarding sparse Bayesian regression.

Forecasting of Spatio-temporal Chaotic Dynamics with Recurrent Neural Networks: a comparative study of Reservoir Computing and Backpropagation Algorithms

How effective are Recurrent Neural Networks (RNNs) in forecasting the spatiotemporal dynamics of chaotic systems ? We address this question through a comparative study of Reservoir Computing (RC) and backpropagation through time (BPTT) algorithms for gated network architectures on a number of benchmark problems. We quantify their relative prediction accuracy on the long-term forecasting of Lorenz-96 and the Kuramoto-Sivashinsky equation and calculation of its Lyapunov spectrum. We discuss their implementation on parallel computers and highlight advantages and limitations of each method. We find that, when the full state dynamics are available for training, RC outperforms BPTT approaches in terms of predictive performance and capturing of the long-term statistics, while at the same time requiring much less time for training. However, in the case of reduced order data, large RC models can be unstable and more likely, than the BPTT algorithms, to diverge in the long term. In contrast, RNNs trained via BPTT capture well the dynamics of these reduced order models. This study confirms that RNNs present a potent computational framework for the forecasting of complex spatio-temporal dynamics.