Discovering and forecasting extreme events via active learning in neural operators

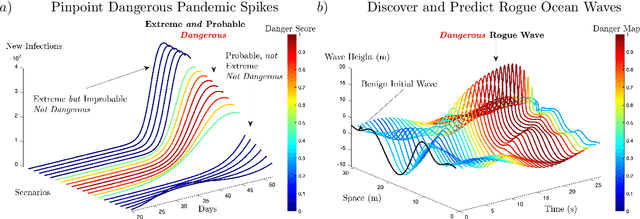
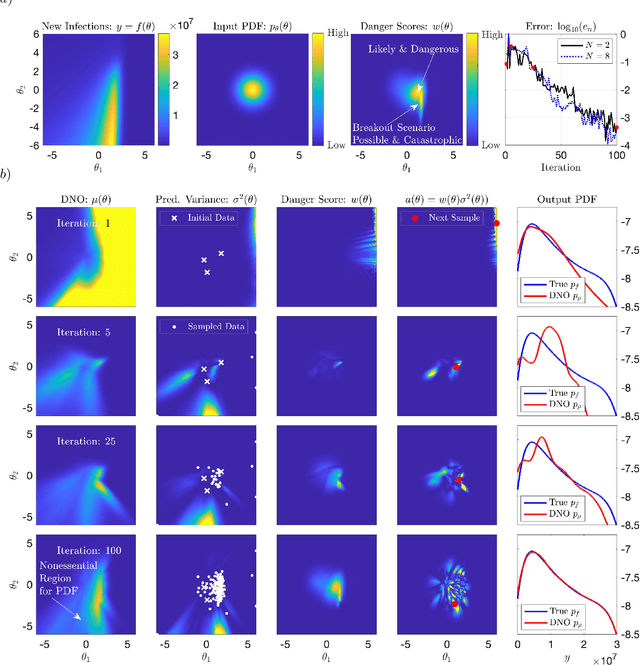
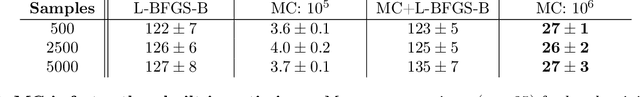
Extreme events in society and nature, such as pandemic spikes or rogue waves, can have catastrophic consequences. Characterizing extremes is difficult as they occur rarely, arise from seemingly benign conditions, and belong to complex and often unknown infinite-dimensional systems. Such challenges render attempts at characterizing them as moot. We address each of these difficulties by combining novel training schemes in Bayesian experimental design (BED) with an ensemble of deep neural operators (DNOs). This model-agnostic framework pairs a BED scheme that actively selects data for quantifying extreme events with an ensemble of DNOs that approximate infinite-dimensional nonlinear operators. We find that not only does this framework clearly beat Gaussian processes (GPs) but that 1) shallow ensembles of just two members perform best; 2) extremes are uncovered regardless of the state of initial data (i.e. with or without extremes); 3) our method eliminates "double-descent" phenomena; 4) the use of batches of suboptimal acquisition points compared to step-by-step global optima does not hinder BED performance; and 5) Monte Carlo acquisition outperforms standard minimizers in high-dimensions. Together these conclusions form the foundation of an AI-assisted experimental infrastructure that can efficiently infer and pinpoint critical situations across many domains, from physical to societal systems.