Biology-informed neural networks learn nonlinear representations from omics data to improve genomic prediction and interpretability

We extend biologically-informed neural networks (BINNs) for genomic prediction (GP) and selection (GS) in crops by integrating thousands of single-nucleotide polymorphisms (SNPs) with multi-omics measurements and prior biological knowledge. Traditional genotype-to-phenotype (G2P) models depend heavily on direct mappings that achieve only modest accuracy, forcing breeders to conduct large, costly field trials to maintain or marginally improve genetic gain. Models that incorporate intermediate molecular phenotypes such as gene expression can achieve higher predictive fit, but they remain impractical for GS since such data are unavailable at deployment or design time. BINNs overcome this limitation by encoding pathway-level inductive biases and leveraging multi-omics data only during training, while using genotype data alone during inference. Applied to maize gene-expression and multi-environment field-trial data, BINN improves rank-correlation accuracy by up to 56% within and across subpopulations under sparse-data conditions and nonlinearly identifies genes that GWAS/TWAS fail to uncover. With complete domain knowledge for a synthetic metabolomics benchmark, BINN reduces prediction error by 75% relative to conventional neural nets and correctly identifies the most important nonlinear pathway. Importantly, both cases show highly sensitive BINN latent variables correlate with the experimental quantities they represent, despite not being trained on them. This suggests BINNs learn biologically-relevant representations, nonlinear or linear, from genotype to phenotype. Together, BINNs establish a framework that leverages intermediate domain information to improve genomic prediction accuracy and reveal nonlinear biological relationships that can guide genomic selection, candidate gene selection, pathway enrichment, and gene-editing prioritization.

Information FOMO: The unhealthy fear of missing out on information. A method for removing misleading data for healthier models

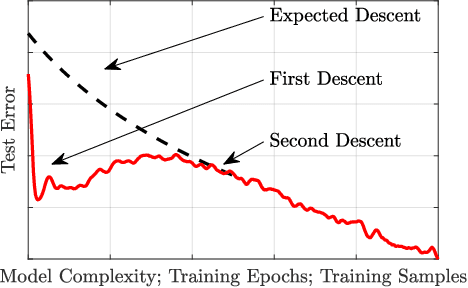
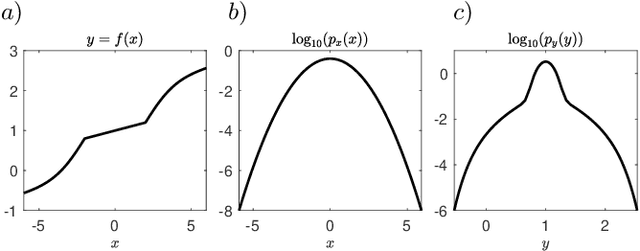
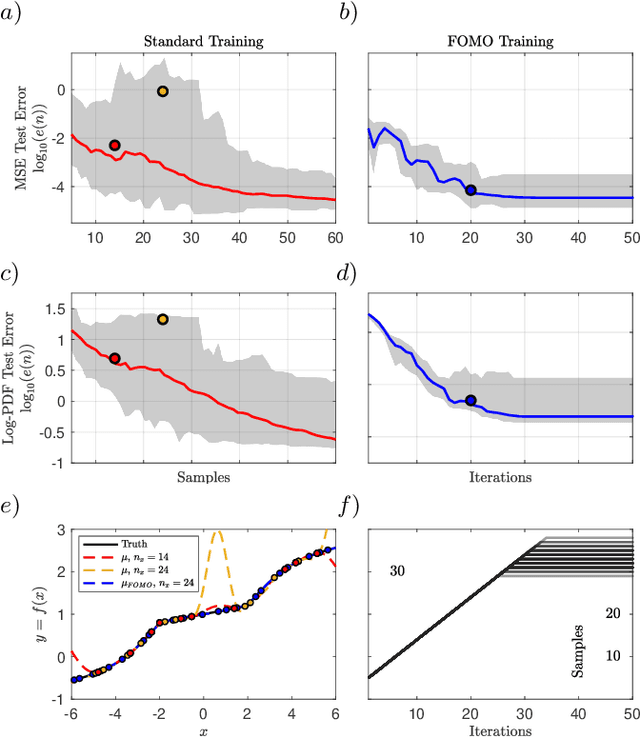
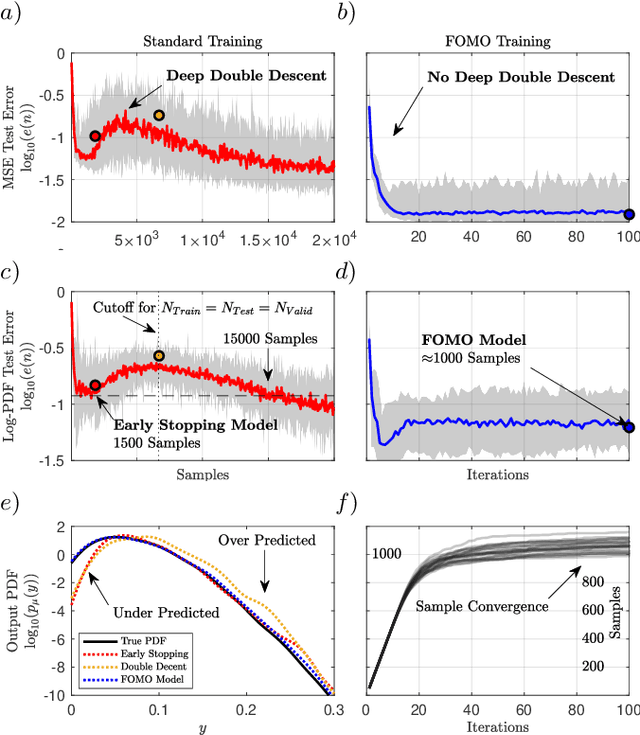
Not all data are equal. Misleading or unnecessary data can critically hinder the accuracy of Machine Learning (ML) models. When data is plentiful, misleading effects can be overcome, but in many real-world applications data is sparse and expensive to acquire. We present a method that substantially reduces the data size necessary to accurately train ML models, potentially opening the door for many new, limited-data applications in ML. Our method extracts the most informative data, while ignoring and omitting data that misleads the ML model to inferior generalization properties. Specifically, the method eliminates the phenomena of "double descent", where more data leads to worse performance. This approach brings several key features to the ML community. Notably, the method naturally converges and removes the traditional need to divide the dataset into training, testing, and validation data. Instead, the selection metric inherently assesses testing error. This ensures that key information is never wasted in testing or validation.

Discovering and forecasting extreme events via active learning in neural operators

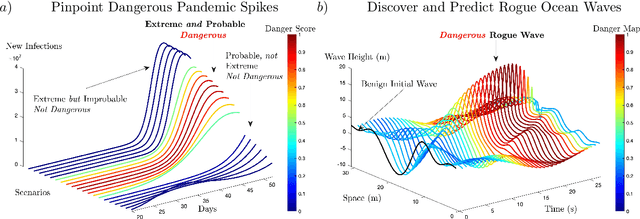
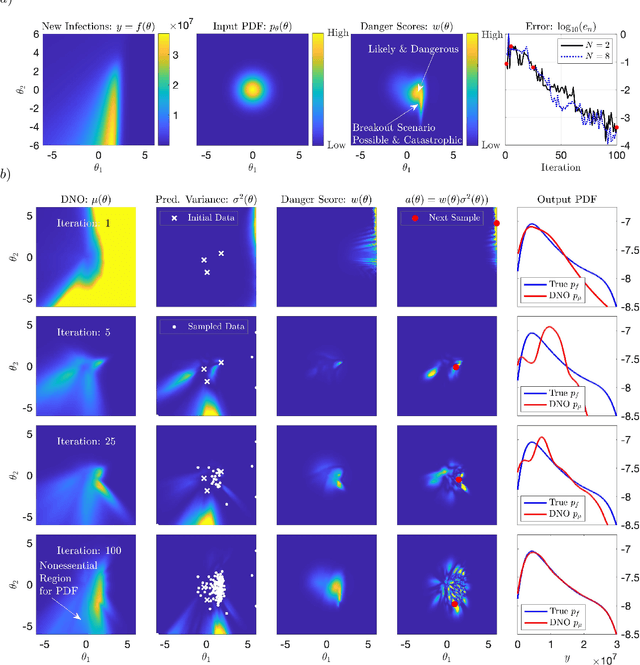
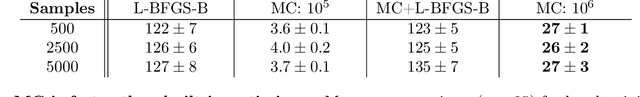
Extreme events in society and nature, such as pandemic spikes or rogue waves, can have catastrophic consequences. Characterizing extremes is difficult as they occur rarely, arise from seemingly benign conditions, and belong to complex and often unknown infinite-dimensional systems. Such challenges render attempts at characterizing them as moot. We address each of these difficulties by combining novel training schemes in Bayesian experimental design (BED) with an ensemble of deep neural operators (DNOs). This model-agnostic framework pairs a BED scheme that actively selects data for quantifying extreme events with an ensemble of DNOs that approximate infinite-dimensional nonlinear operators. We find that not only does this framework clearly beat Gaussian processes (GPs) but that 1) shallow ensembles of just two members perform best; 2) extremes are uncovered regardless of the state of initial data (i.e. with or without extremes); 3) our method eliminates "double-descent" phenomena; 4) the use of batches of suboptimal acquisition points compared to step-by-step global optima does not hinder BED performance; and 5) Monte Carlo acquisition outperforms standard minimizers in high-dimensions. Together these conclusions form the foundation of an AI-assisted experimental infrastructure that can efficiently infer and pinpoint critical situations across many domains, from physical to societal systems.

Structure and Distribution Metric for Quantifying the Quality of Uncertainty: Assessing Gaussian Processes, Deep Neural Nets, and Deep Neural Operators for Regression

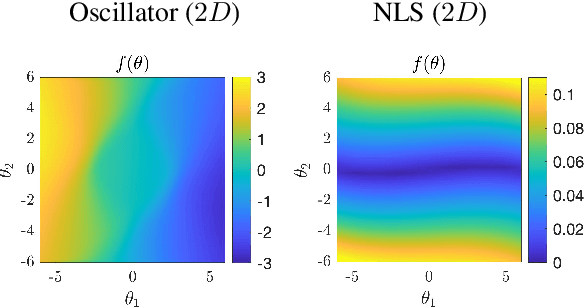
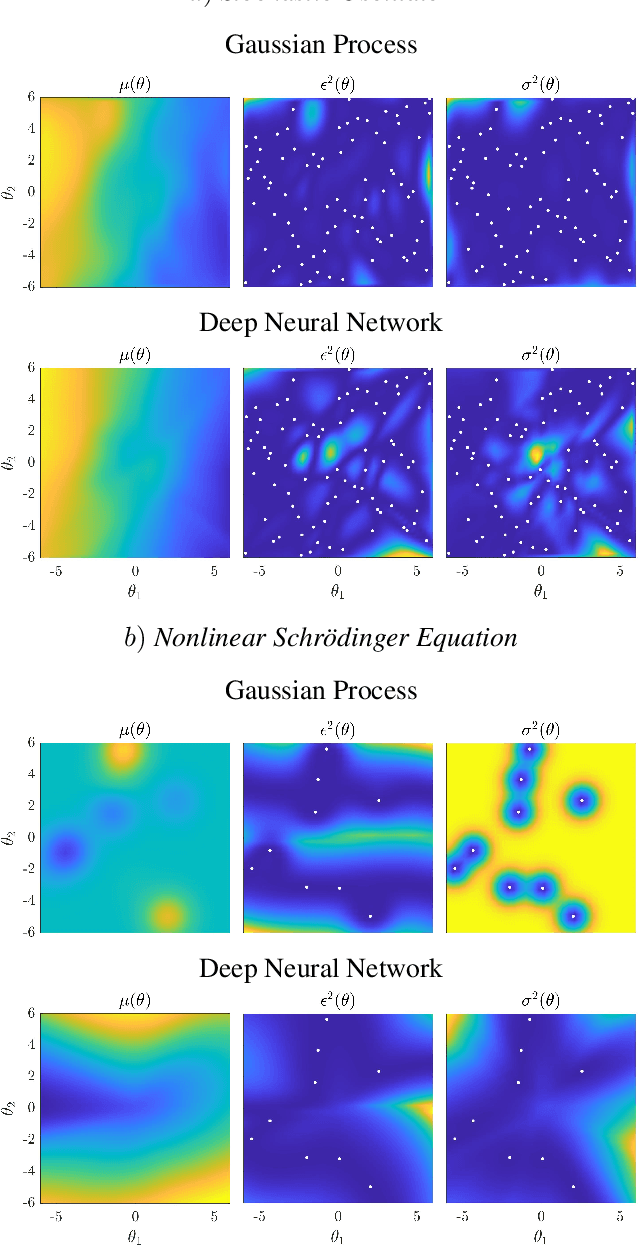
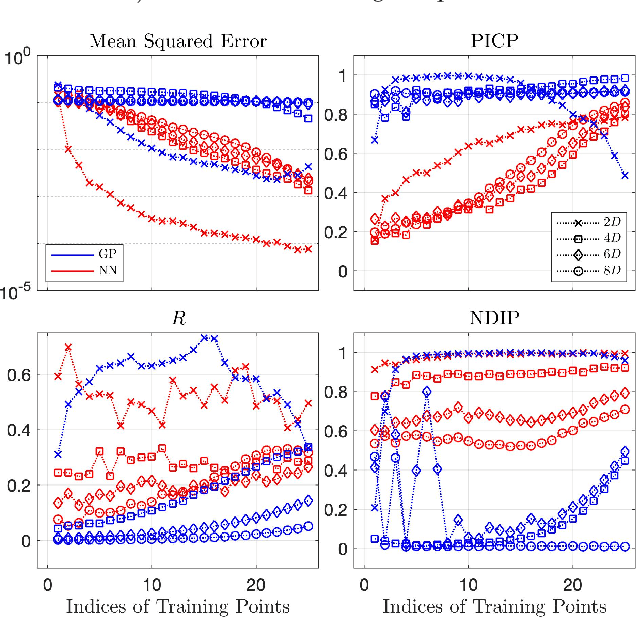
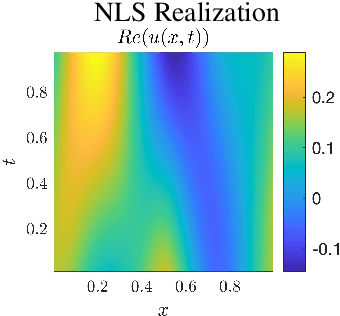
We propose two bounded comparison metrics that may be implemented to arbitrary dimensions in regression tasks. One quantifies the structure of uncertainty and the other quantifies the distribution of uncertainty. The structure metric assesses the similarity in shape and location of uncertainty with the true error, while the distribution metric quantifies the supported magnitudes between the two. We apply these metrics to Gaussian Processes (GPs), Ensemble Deep Neural Nets (DNNs), and Ensemble Deep Neural Operators (DNOs) on high-dimensional and nonlinear test cases. We find that comparing a model's uncertainty estimates with the model's squared error provides a compelling ground truth assessment. We also observe that both DNNs and DNOs, especially when compared to GPs, provide encouraging metric values in high dimensions with either sparse or plentiful data.