Synergistic Learning with Multi-Task DeepONet for Efficient PDE Problem Solving

Multi-task learning (MTL) is an inductive transfer mechanism designed to leverage useful information from multiple tasks to improve generalization performance compared to single-task learning. It has been extensively explored in traditional machine learning to address issues such as data sparsity and overfitting in neural networks. In this work, we apply MTL to problems in science and engineering governed by partial differential equations (PDEs). However, implementing MTL in this context is complex, as it requires task-specific modifications to accommodate various scenarios representing different physical processes. To this end, we present a multi-task deep operator network (MT-DeepONet) to learn solutions across various functional forms of source terms in a PDE and multiple geometries in a single concurrent training session. We introduce modifications in the branch network of the vanilla DeepONet to account for various functional forms of a parameterized coefficient in a PDE. Additionally, we handle parameterized geometries by introducing a binary mask in the branch network and incorporating it into the loss term to improve convergence and generalization to new geometry tasks. Our approach is demonstrated on three benchmark problems: (1) learning different functional forms of the source term in the Fisher equation; (2) learning multiple geometries in a 2D Darcy Flow problem and showcasing better transfer learning capabilities to new geometries; and (3) learning 3D parameterized geometries for a heat transfer problem and demonstrate the ability to predict on new but similar geometries. Our MT-DeepONet framework offers a novel approach to solving PDE problems in engineering and science under a unified umbrella based on synergistic learning that reduces the overall training cost for neural operators.

Learning in latent spaces improves the predictive accuracy of deep neural operators

Operator regression provides a powerful means of constructing discretization-invariant emulators for partial-differential equations (PDEs) describing physical systems. Neural operators specifically employ deep neural networks to approximate mappings between infinite-dimensional Banach spaces. As data-driven models, neural operators require the generation of labeled observations, which in cases of complex high-fidelity models result in high-dimensional datasets containing redundant and noisy features, which can hinder gradient-based optimization. Mapping these high-dimensional datasets to a low-dimensional latent space of salient features can make it easier to work with the data and also enhance learning. In this work, we investigate the latent deep operator network (L-DeepONet), an extension of standard DeepONet, which leverages latent representations of high-dimensional PDE input and output functions identified with suitable autoencoders. We illustrate that L-DeepONet outperforms the standard approach in terms of both accuracy and computational efficiency across diverse time-dependent PDEs, e.g., modeling the growth of fracture in brittle materials, convective fluid flows, and large-scale atmospheric flows exhibiting multiscale dynamical features.

Deep transfer learning for partial differential equations under conditional shift with DeepONet

Traditional machine learning algorithms are designed to learn in isolation, i.e. address single tasks. The core idea of transfer learning (TL) is that knowledge gained in learning to perform one task (source) can be leveraged to improve learning performance in a related, but different, task (target). TL leverages and transfers previously acquired knowledge to address the expense of data acquisition and labeling, potential computational power limitations, and the dataset distribution mismatches. Although significant progress has been made in the fields of image processing, speech recognition, and natural language processing (for classification and regression) for TL, little work has been done in the field of scientific machine learning for functional regression and uncertainty quantification in partial differential equations. In this work, we propose a novel TL framework for task-specific learning under conditional shift with a deep operator network (DeepONet). Inspired by the conditional embedding operator theory, we measure the statistical distance between the source domain and the target feature domain by embedding conditional distributions onto a reproducing kernel Hilbert space. Task-specific operator learning is accomplished by fine-tuning task-specific layers of the target DeepONet using a hybrid loss function that allows for the matching of individual target samples while also preserving the global properties of the conditional distribution of target data. We demonstrate the advantages of our approach for various TL scenarios involving nonlinear PDEs under conditional shift. Our results include geometry domain adaptation and show that the proposed TL framework enables fast and efficient multi-task operator learning, despite significant differences between the source and target domains.

On the influence of over-parameterization in manifold based surrogates and deep neural operators

Constructing accurate and generalizable approximators for complex physico-chemical processes exhibiting highly non-smooth dynamics is challenging. In this work, we propose new developments and perform comparisons for two promising approaches: manifold-based polynomial chaos expansion (m-PCE) and the deep neural operator (DeepONet), and we examine the effect of over-parameterization on generalization. We demonstrate the performance of these methods in terms of generalization accuracy by solving the 2D time-dependent Brusselator reaction-diffusion system with uncertainty sources, modeling an autocatalytic chemical reaction between two species. We first propose an extension of the m-PCE by constructing a mapping between latent spaces formed by two separate embeddings of input functions and output QoIs. To enhance the accuracy of the DeepONet, we introduce weight self-adaptivity in the loss function. We demonstrate that the performance of m-PCE and DeepONet is comparable for cases of relatively smooth input-output mappings. However, when highly non-smooth dynamics is considered, DeepONet shows higher accuracy. We also find that for m-PCE, modest over-parameterization leads to better generalization, both within and outside of distribution, whereas aggressive over-parameterization leads to over-fitting. In contrast, an even highly over-parameterized DeepONet leads to better generalization for both smooth and non-smooth dynamics. Furthermore, we compare the performance of the above models with another operator learning model, the Fourier Neural Operator, and show that its over-parameterization also leads to better generalization. Our studies show that m-PCE can provide very good accuracy at very low training cost, whereas a highly over-parameterized DeepONet can provide better accuracy and robustness to noise but at higher training cost. In both methods, the inference cost is negligible.

A survey of unsupervised learning methods for high-dimensional uncertainty quantification in black-box-type problems

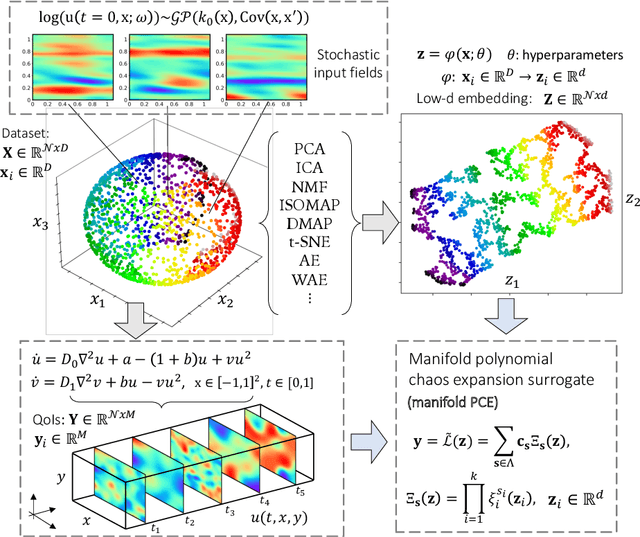
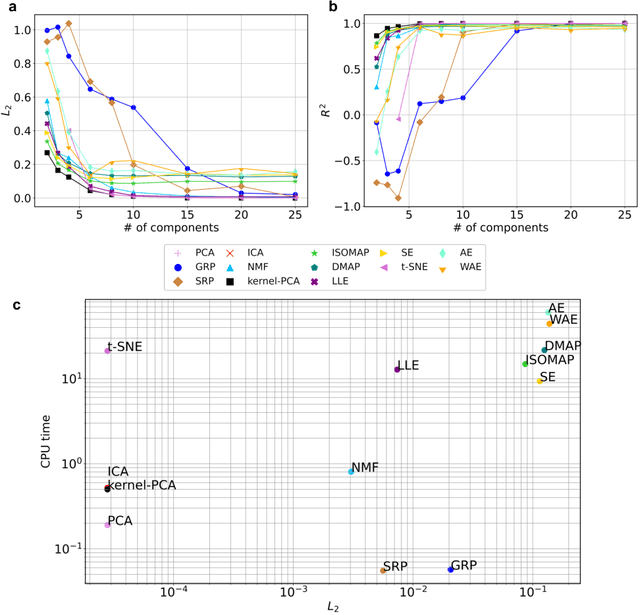
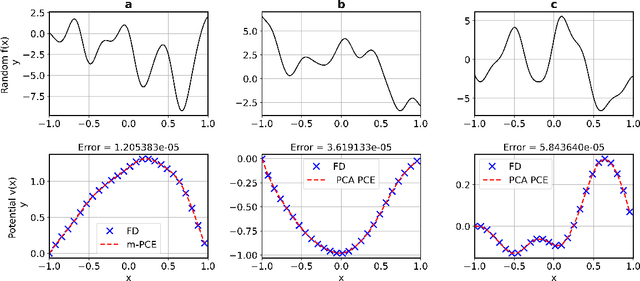
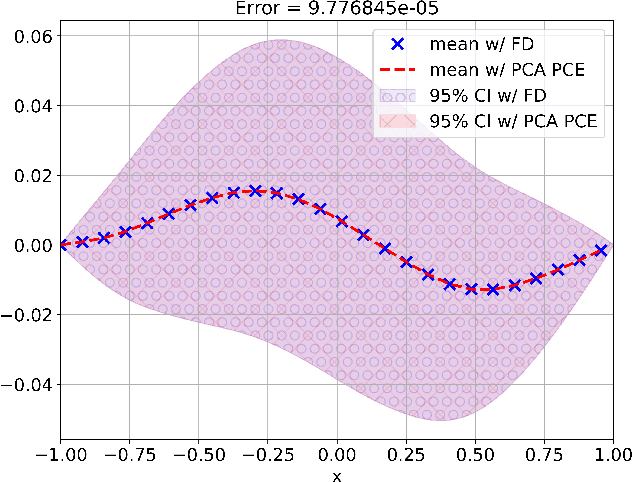
Constructing surrogate models for uncertainty quantification (UQ) on complex partial differential equations (PDEs) having inherently high-dimensional $\mathcal{O}(10^{\ge 2})$ stochastic inputs (e.g., forcing terms, boundary conditions, initial conditions) poses tremendous challenges. The curse of dimensionality can be addressed with suitable unsupervised learning techniques used as a pre-processing tool to encode inputs onto lower-dimensional subspaces while retaining its structural information and meaningful properties. In this work, we review and investigate thirteen dimension reduction methods including linear and nonlinear, spectral, blind source separation, convex and non-convex methods and utilize the resulting embeddings to construct a mapping to quantities of interest via polynomial chaos expansions (PCE). We refer to the general proposed approach as manifold PCE (m-PCE), where manifold corresponds to the latent space resulting from any of the studied dimension reduction methods. To investigate the capabilities and limitations of these methods we conduct numerical tests for three physics-based systems (treated as black-boxes) having high-dimensional stochastic inputs of varying complexity modeled as both Gaussian and non-Gaussian random fields to investigate the effect of the intrinsic dimensionality of input data. We demonstrate both the advantages and limitations of the unsupervised learning methods and we conclude that a suitable m-PCE model provides a cost-effective approach compared to alternative algorithms proposed in the literature, including recently proposed expensive deep neural network-based surrogates and can be readily applied for high-dimensional UQ in stochastic PDEs.

Grassmannian diffusion maps based surrogate modeling via geometric harmonics

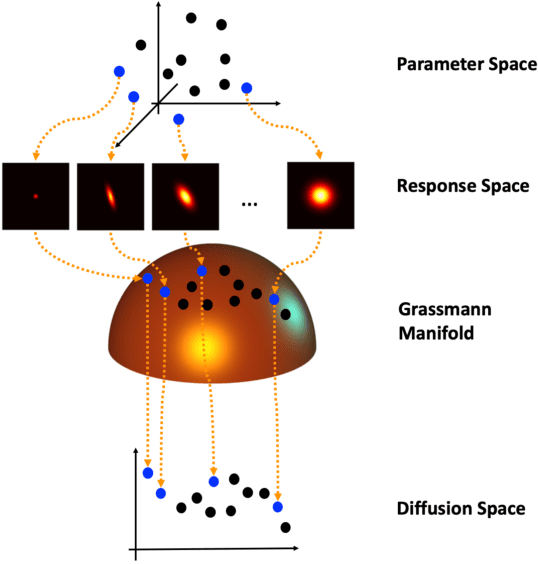
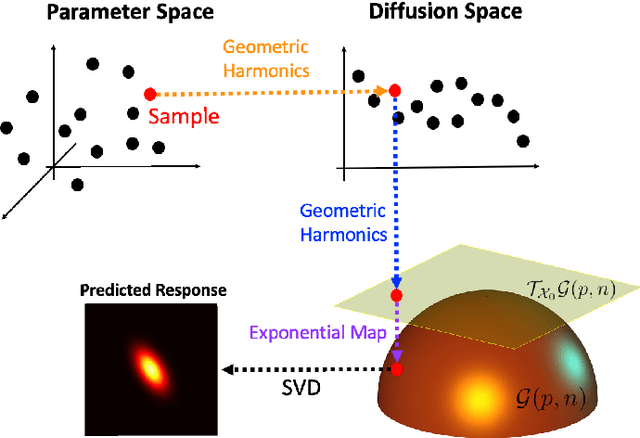
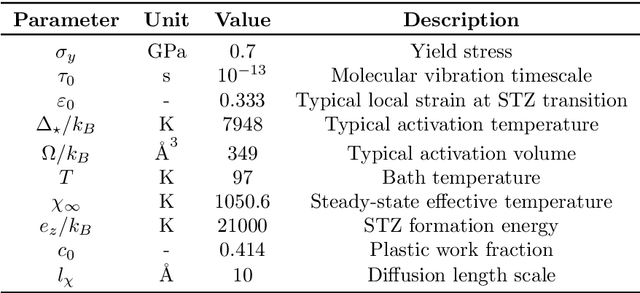
In this paper, a novel surrogate model based on the Grassmannian diffusion maps (GDMaps) and utilizing geometric harmonics is developed for predicting the response of engineering systems and complex physical phenomena. The method utilizes the GDMaps to obtain a low-dimensional representation of the underlying behavior of physical/mathematical systems with respect to uncertainties in the input parameters. Using this representation, geometric harmonics, an out-of-sample function extension technique, is employed to create a global map from the space of input parameters to a Grassmannian diffusion manifold. Geometric harmonics is also employed to locally map points on the diffusion manifold onto the tangent space of a Grassmann manifold. The exponential map is then used to project the points in the tangent space onto the Grassmann manifold, where reconstruction of the full solution is performed. The performance of the proposed surrogate modeling is verified with three examples. The first problem is a toy example used to illustrate the development of the technique. In the second example, errors associated with the various mappings employed in the technique are assessed by studying response predictions of the electric potential of a dielectric cylinder in a homogeneous electric field. The last example applies the method for uncertainty prediction in the strain field evolution in a model amorphous material using the shear transformation zone (STZ) theory of plasticity. In all examples, accurate predictions are obtained, showing that the present technique is a strong candidate for the application of uncertainty quantification in large-scale models.

Neural density estimation and uncertainty quantification for laser induced breakdown spectroscopy spectra

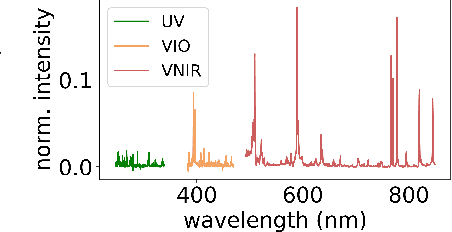
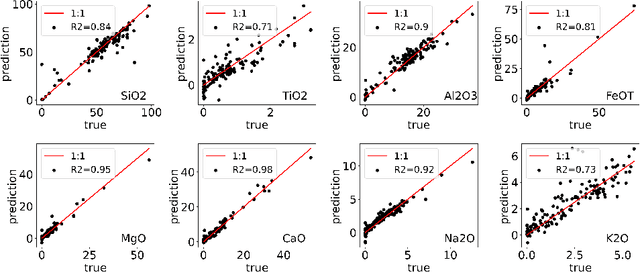
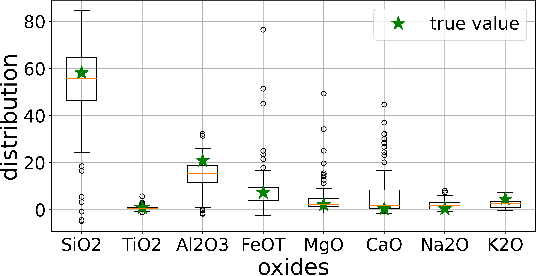
Constructing probability densities for inference in high-dimensional spectral data is often intractable. In this work, we use normalizing flows on structured spectral latent spaces to estimate such densities, enabling downstream inference tasks. In addition, we evaluate a method for uncertainty quantification when predicting unobserved state vectors associated with each spectrum. We demonstrate the capability of this approach on laser-induced breakdown spectroscopy data collected by the ChemCam instrument on the Mars rover Curiosity. Using our approach, we are able to generate realistic spectral samples and to accurately predict state vectors with associated well-calibrated uncertainties. We anticipate that this methodology will enable efficient probabilistic modeling of spectral data, leading to potential advances in several areas, including out-of-distribution detection and sensitivity analysis.

Manifold learning-based polynomial chaos expansions for high-dimensional surrogate models

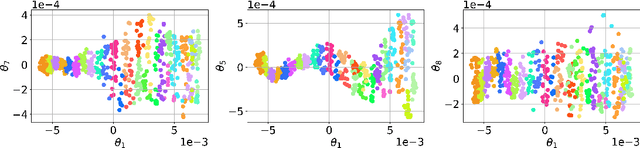
In this work we introduce a manifold learning-based method for uncertainty quantification (UQ) in systems describing complex spatiotemporal processes. Our first objective is to identify the embedding of a set of high-dimensional data representing quantities of interest of the computational or analytical model. For this purpose, we employ Grassmannian diffusion maps, a two-step nonlinear dimension reduction technique which allows us to reduce the dimensionality of the data and identify meaningful geometric descriptions in a parsimonious and inexpensive manner. Polynomial chaos expansion is then used to construct a mapping between the stochastic input parameters and the diffusion coordinates of the reduced space. An adaptive clustering technique is proposed to identify an optimal number of clusters of points in the latent space. The similarity of points allows us to construct a number of geometric harmonic emulators which are finally utilized as a set of inexpensive pre-trained models to perform an inverse map of realizations of latent features to the ambient space and thus perform accurate out-of-sample predictions. Thus, the proposed method acts as an encoder-decoder system which is able to automatically handle very high-dimensional data while simultaneously operating successfully in the small-data regime. The method is demonstrated on two benchmark problems and on a system of advection-diffusion-reaction equations which model a first-order chemical reaction between two species. In all test cases, the proposed method is able to achieve highly accurate approximations which ultimately lead to the significant acceleration of UQ tasks.