Implementing LLMs in industrial process modeling: Addressing Categorical Variables

Important variables of processes are, in many occasions, categorical, i.e. names or labels representing, e.g. categories of inputs, or types of reactors or a sequence of steps. In this work, we use Large Language Models (LLMs) to derive embeddings of such inputs that represent their actual meaning, or reflect the ``distances" between categories, i.e. how similar or dissimilar they are. This is a marked difference from the current standard practice of using binary, or one-hot encoding to replace categorical variables with sequences of ones and zeros. Combined with dimensionality reduction techniques, either linear such as Principal Components Analysis (PCA), or nonlinear such as Uniform Manifold Approximation and Projection (UMAP), the proposed approach leads to a \textit{meaningful}, low-dimensional feature space. The significance of obtaining meaningful embeddings is illustrated in the context of an industrial coating process for cutting tools that includes both numerical and categorical inputs. The proposed approach enables feature importance which is a marked improvement compared to the current state-of-the-art (SotA) in the encoding of categorical variables.

Discovering deposition process regimes: leveraging unsupervised learning for process insights, surrogate modeling, and sensitivity analysis

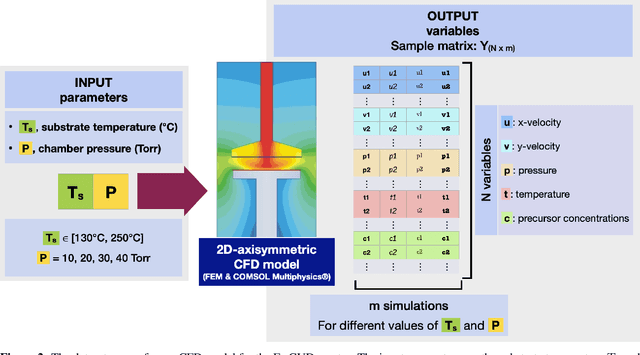
This work introduces a comprehensive approach utilizing data-driven methods to elucidate the deposition process regimes in Chemical Vapor Deposition (CVD) reactors and the interplay of physical mechanism that dominate in each one of them. Through this work, we address three key objectives. Firstly, our methodology relies on process outcomes, derived by a detailed CFD model, to identify clusters of "outcomes" corresponding to distinct process regimes, wherein the relative influence of input variables undergoes notable shifts. This phenomenon is experimentally validated through Arrhenius plot analysis, affirming the efficacy of our approach. Secondly, we demonstrate the development of an efficient surrogate model, based on Polynomial Chaos Expansion (PCE), that maintains accuracy, facilitating streamlined computational analyses. Finally, as a result of PCE, sensitivity analysis is made possible by means of Sobol' indices, that quantify the impact of process inputs across identified regimes. The insights gained from our analysis contribute to the formulation of hypotheses regarding phenomena occurring beyond the transition regime. Notably, the significance of temperature even in the diffusion-limited regime, as evidenced by the Arrhenius plot, suggests activation of gas phase reactions at elevated temperatures. Importantly, our proposed methods yield insights that align with experimental observations and theoretical principles, aiding decision-making in process design and optimization. By circumventing the need for costly and time-consuming experiments, our approach offers a pragmatic pathway towards enhanced process efficiency. Moreover, this study underscores the potential of data-driven computational methods for innovating reactor design paradigms.

Integrating supervised and unsupervised learning approaches to unveil critical process inputs

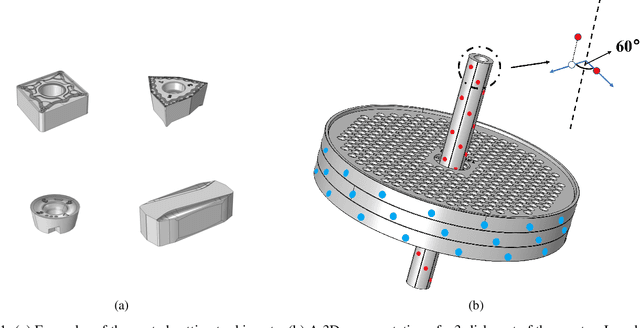
This study introduces a machine learning framework tailored to large-scale industrial processes characterized by a plethora of numerical and categorical inputs. The framework aims to (i) discern critical parameters influencing the output and (ii) generate accurate out-of-sample qualitative and quantitative predictions of production outcomes. Specifically, we address the pivotal question of the significance of each input in shaping the process outcome, using an industrial Chemical Vapor Deposition (CVD) process as an example. The initial objective involves merging subject matter expertise and clustering techniques exclusively on the process output, here, coating thickness measurements at various positions in the reactor. This approach identifies groups of production runs that share similar qualitative characteristics, such as film mean thickness and standard deviation. In particular, the differences of the outcomes represented by the different clusters can be attributed to differences in specific inputs, indicating that these inputs are critical for the production outcome. Leveraging this insight, we subsequently implement supervised classification and regression methods using the identified critical process inputs. The proposed methodology proves to be valuable in scenarios with a multitude of inputs and insufficient data for the direct application of deep learning techniques, providing meaningful insights into the underlying processes.

Machine Learning for the identification of phase-transitions in interacting agent-based systems

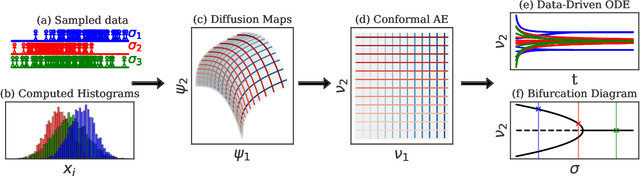
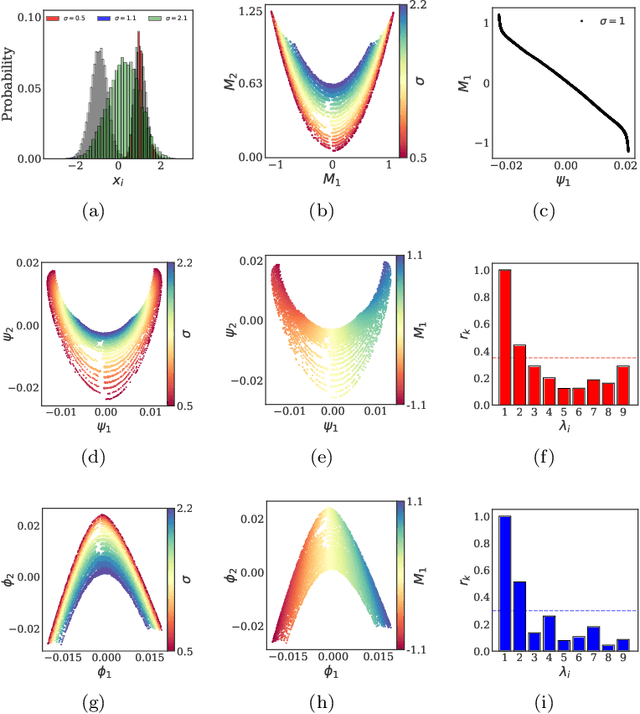
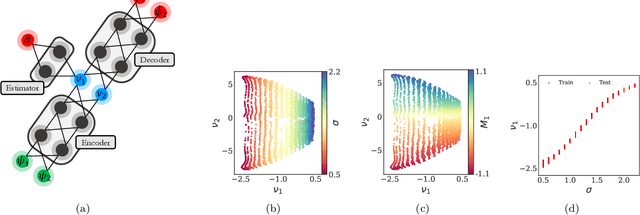
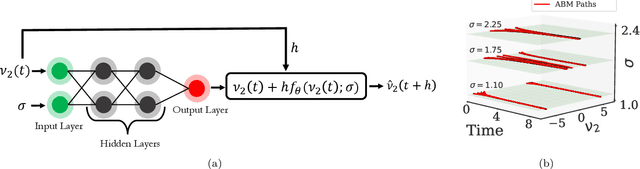
Deriving closed-form, analytical expressions for reduced-order models, and judiciously choosing the closures leading to them, has long been the strategy of choice for studying phase- and noise-induced transitions for agent-based models (ABMs). In this paper, we propose a data-driven framework that pinpoints phase transitions for an ABM in its mean-field limit, using a smaller number of variables than traditional closed-form models. To this end, we use the manifold learning algorithm Diffusion Maps to identify a parsimonious set of data-driven latent variables, and show that they are in one-to-one correspondence with the expected theoretical order parameter of the ABM. We then utilize a deep learning framework to obtain a conformal reparametrization of the data-driven coordinates that facilitates, in our example, the identification of a single parameter-dependent ODE in these coordinates. We identify this ODE through a residual neural network inspired by a numerical integration scheme (forward Euler). We then use the identified ODE -- enabled through an odd symmetry transformation -- to construct the bifurcation diagram exhibiting the phase transition.

Grassmannian diffusion maps based surrogate modeling via geometric harmonics

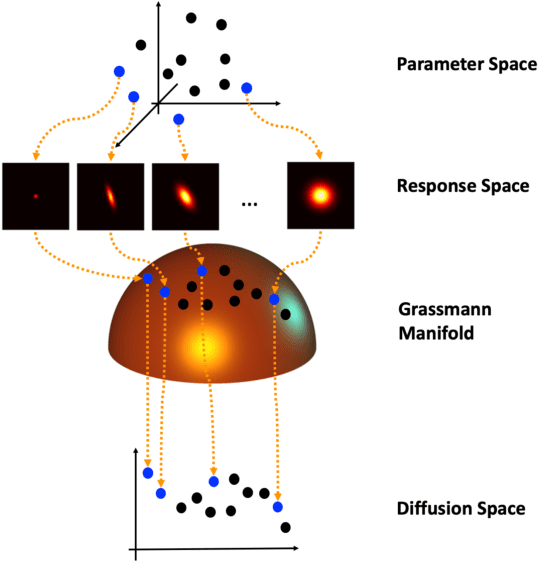
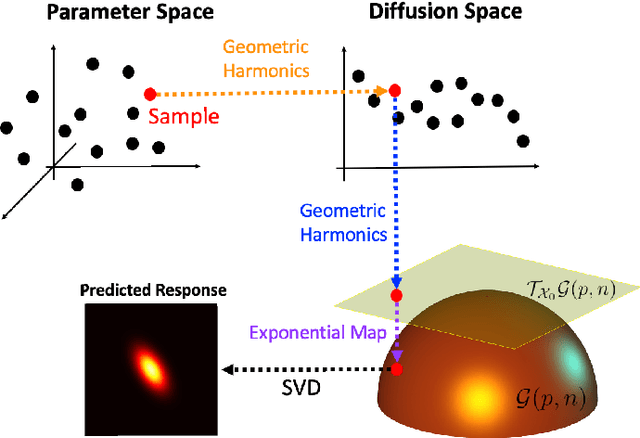
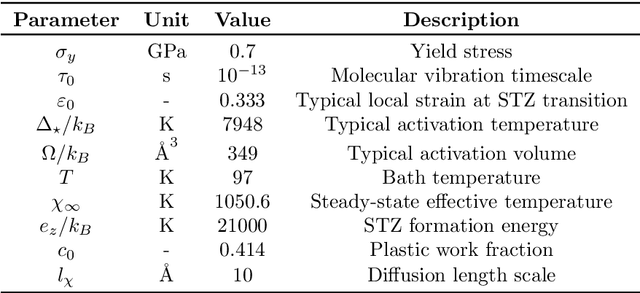
In this paper, a novel surrogate model based on the Grassmannian diffusion maps (GDMaps) and utilizing geometric harmonics is developed for predicting the response of engineering systems and complex physical phenomena. The method utilizes the GDMaps to obtain a low-dimensional representation of the underlying behavior of physical/mathematical systems with respect to uncertainties in the input parameters. Using this representation, geometric harmonics, an out-of-sample function extension technique, is employed to create a global map from the space of input parameters to a Grassmannian diffusion manifold. Geometric harmonics is also employed to locally map points on the diffusion manifold onto the tangent space of a Grassmann manifold. The exponential map is then used to project the points in the tangent space onto the Grassmann manifold, where reconstruction of the full solution is performed. The performance of the proposed surrogate modeling is verified with three examples. The first problem is a toy example used to illustrate the development of the technique. In the second example, errors associated with the various mappings employed in the technique are assessed by studying response predictions of the electric potential of a dielectric cylinder in a homogeneous electric field. The last example applies the method for uncertainty prediction in the strain field evolution in a model amorphous material using the shear transformation zone (STZ) theory of plasticity. In all examples, accurate predictions are obtained, showing that the present technique is a strong candidate for the application of uncertainty quantification in large-scale models.

Manifold learning-based polynomial chaos expansions for high-dimensional surrogate models

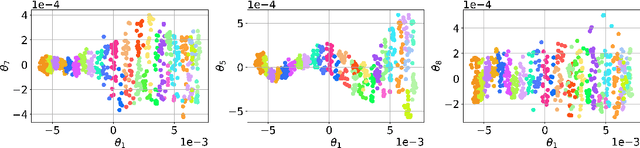
In this work we introduce a manifold learning-based method for uncertainty quantification (UQ) in systems describing complex spatiotemporal processes. Our first objective is to identify the embedding of a set of high-dimensional data representing quantities of interest of the computational or analytical model. For this purpose, we employ Grassmannian diffusion maps, a two-step nonlinear dimension reduction technique which allows us to reduce the dimensionality of the data and identify meaningful geometric descriptions in a parsimonious and inexpensive manner. Polynomial chaos expansion is then used to construct a mapping between the stochastic input parameters and the diffusion coordinates of the reduced space. An adaptive clustering technique is proposed to identify an optimal number of clusters of points in the latent space. The similarity of points allows us to construct a number of geometric harmonic emulators which are finally utilized as a set of inexpensive pre-trained models to perform an inverse map of realizations of latent features to the ambient space and thus perform accurate out-of-sample predictions. Thus, the proposed method acts as an encoder-decoder system which is able to automatically handle very high-dimensional data while simultaneously operating successfully in the small-data regime. The method is demonstrated on two benchmark problems and on a system of advection-diffusion-reaction equations which model a first-order chemical reaction between two species. In all test cases, the proposed method is able to achieve highly accurate approximations which ultimately lead to the significant acceleration of UQ tasks.