Grassmannian diffusion maps based surrogate modeling via geometric harmonics

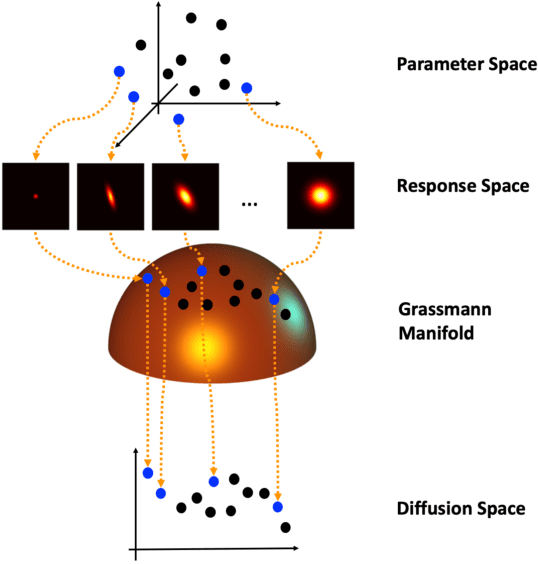
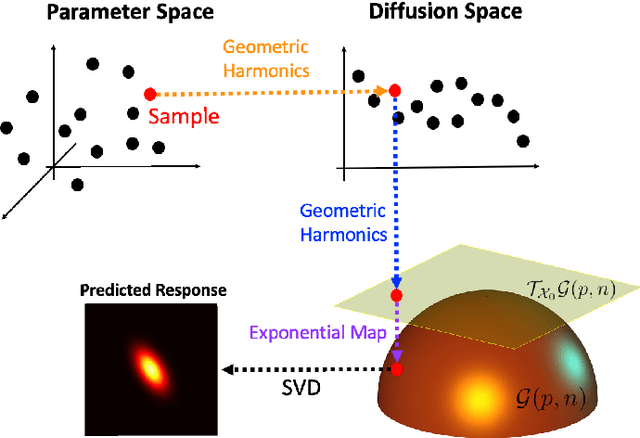
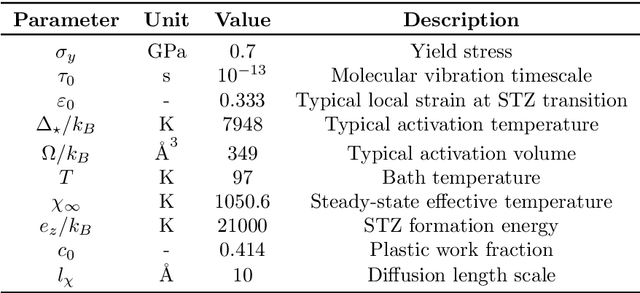
In this paper, a novel surrogate model based on the Grassmannian diffusion maps (GDMaps) and utilizing geometric harmonics is developed for predicting the response of engineering systems and complex physical phenomena. The method utilizes the GDMaps to obtain a low-dimensional representation of the underlying behavior of physical/mathematical systems with respect to uncertainties in the input parameters. Using this representation, geometric harmonics, an out-of-sample function extension technique, is employed to create a global map from the space of input parameters to a Grassmannian diffusion manifold. Geometric harmonics is also employed to locally map points on the diffusion manifold onto the tangent space of a Grassmann manifold. The exponential map is then used to project the points in the tangent space onto the Grassmann manifold, where reconstruction of the full solution is performed. The performance of the proposed surrogate modeling is verified with three examples. The first problem is a toy example used to illustrate the development of the technique. In the second example, errors associated with the various mappings employed in the technique are assessed by studying response predictions of the electric potential of a dielectric cylinder in a homogeneous electric field. The last example applies the method for uncertainty prediction in the strain field evolution in a model amorphous material using the shear transformation zone (STZ) theory of plasticity. In all examples, accurate predictions are obtained, showing that the present technique is a strong candidate for the application of uncertainty quantification in large-scale models.

Manifold learning-based polynomial chaos expansions for high-dimensional surrogate models

In this work we introduce a manifold learning-based method for uncertainty quantification (UQ) in systems describing complex spatiotemporal processes. Our first objective is to identify the embedding of a set of high-dimensional data representing quantities of interest of the computational or analytical model. For this purpose, we employ Grassmannian diffusion maps, a two-step nonlinear dimension reduction technique which allows us to reduce the dimensionality of the data and identify meaningful geometric descriptions in a parsimonious and inexpensive manner. Polynomial chaos expansion is then used to construct a mapping between the stochastic input parameters and the diffusion coordinates of the reduced space. An adaptive clustering technique is proposed to identify an optimal number of clusters of points in the latent space. The similarity of points allows us to construct a number of geometric harmonic emulators which are finally utilized as a set of inexpensive pre-trained models to perform an inverse map of realizations of latent features to the ambient space and thus perform accurate out-of-sample predictions. Thus, the proposed method acts as an encoder-decoder system which is able to automatically handle very high-dimensional data while simultaneously operating successfully in the small-data regime. The method is demonstrated on two benchmark problems and on a system of advection-diffusion-reaction equations which model a first-order chemical reaction between two species. In all test cases, the proposed method is able to achieve highly accurate approximations which ultimately lead to the significant acceleration of UQ tasks.