A survey of unsupervised learning methods for high-dimensional uncertainty quantification in black-box-type problems
Paper and Code
Feb 09, 2022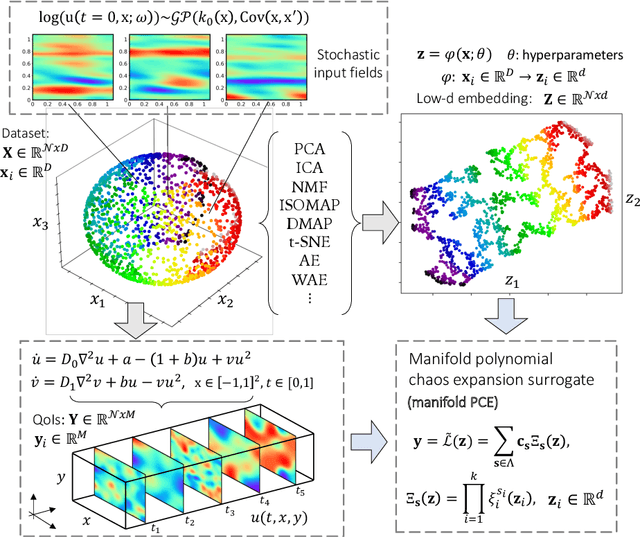
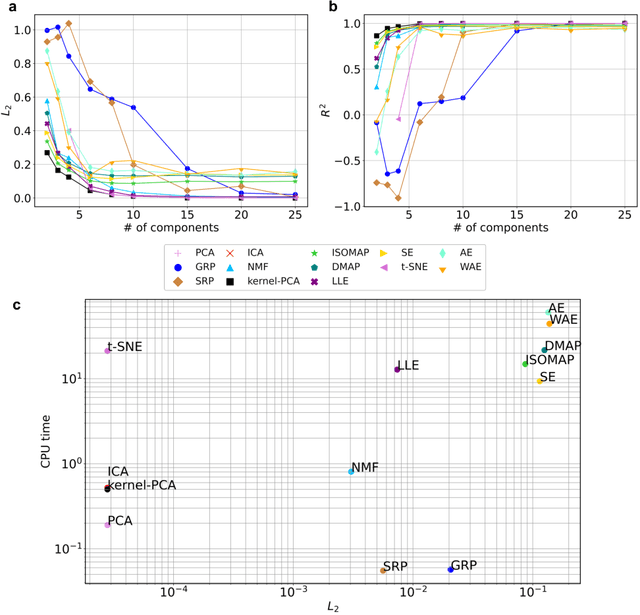
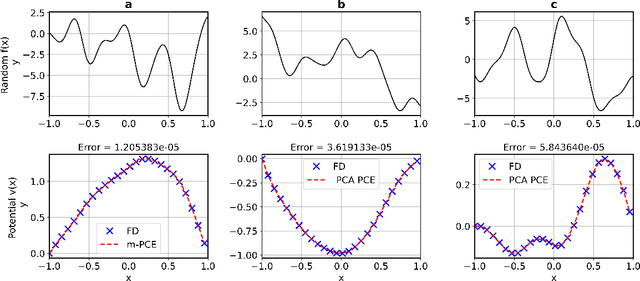
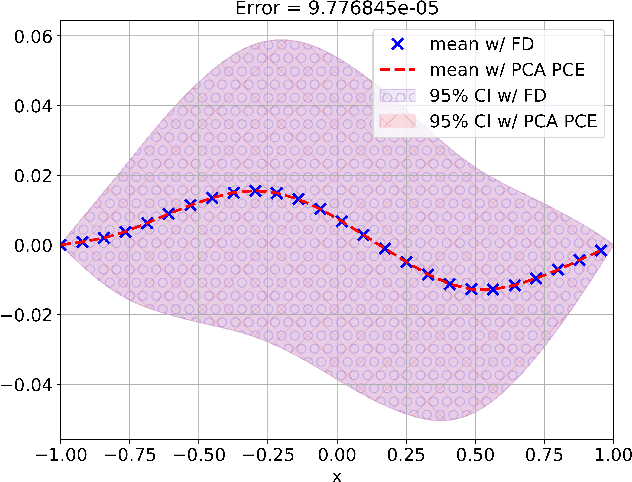
Constructing surrogate models for uncertainty quantification (UQ) on complex partial differential equations (PDEs) having inherently high-dimensional $\mathcal{O}(10^{\ge 2})$ stochastic inputs (e.g., forcing terms, boundary conditions, initial conditions) poses tremendous challenges. The curse of dimensionality can be addressed with suitable unsupervised learning techniques used as a pre-processing tool to encode inputs onto lower-dimensional subspaces while retaining its structural information and meaningful properties. In this work, we review and investigate thirteen dimension reduction methods including linear and nonlinear, spectral, blind source separation, convex and non-convex methods and utilize the resulting embeddings to construct a mapping to quantities of interest via polynomial chaos expansions (PCE). We refer to the general proposed approach as manifold PCE (m-PCE), where manifold corresponds to the latent space resulting from any of the studied dimension reduction methods. To investigate the capabilities and limitations of these methods we conduct numerical tests for three physics-based systems (treated as black-boxes) having high-dimensional stochastic inputs of varying complexity modeled as both Gaussian and non-Gaussian random fields to investigate the effect of the intrinsic dimensionality of input data. We demonstrate both the advantages and limitations of the unsupervised learning methods and we conclude that a suitable m-PCE model provides a cost-effective approach compared to alternative algorithms proposed in the literature, including recently proposed expensive deep neural network-based surrogates and can be readily applied for high-dimensional UQ in stochastic PDEs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge