PINN-FEM: A Hybrid Approach for Enforcing Dirichlet Boundary Conditions in Physics-Informed Neural Networks

Physics-Informed Neural Networks (PINNs) solve partial differential equations (PDEs) by embedding governing equations and boundary/initial conditions into the loss function. However, enforcing Dirichlet boundary conditions accurately remains challenging, often leading to soft enforcement that compromises convergence and reliability in complex domains. We propose a hybrid approach, PINN-FEM, which combines PINNs with finite element methods (FEM) to impose strong Dirichlet boundary conditions via domain decomposition. This method incorporates FEM-based representations near the boundary, ensuring exact enforcement without compromising convergence. Through six experiments of increasing complexity, PINN-FEM outperforms standard PINN models, showcasing superior accuracy and robustness. While distance functions and similar techniques have been proposed for boundary condition enforcement, they lack generality for real-world applications. PINN-FEM bridges this gap by leveraging FEM near boundaries, making it well-suited for industrial and scientific problems.

A Multi-Fidelity Graph U-Net Model for Accelerated Physics Simulations

Physics-based deep learning frameworks have shown to be effective in accurately modeling the dynamics of complex physical systems with generalization capability across problem inputs. Data-driven networks like GNN, Neural Operators have proved to be very effective in generalizing the model across unseen domain and resolutions. But one of the most critical issues in these data-based models is the computational cost of generating training datasets. Complex phenomena can only be captured accurately using deep networks with large training datasets. Furthermore, numerical error of training samples is propagated in the model errors, thus requiring the need for accurate data, i.e. FEM solutions on high-resolution meshes. Multi-fidelity methods offer a potential solution to reduce the training data requirements. To this end, we propose a novel GNN architecture, Multi-Fidelity U-Net, that utilizes the advantages of the multi-fidelity methods for enhancing the performance of the GNN model. The proposed architecture utilizes the capability of GNNs to manage complex geometries across different fidelity levels, while enabling flow of information between these levels for improved prediction accuracy for high-fidelity graphs. We show that the proposed approach performs significantly better in accuracy and data requirement and only requires training of a single network compared to other benchmark multi-fidelity approaches like transfer learning. We also present Multi-Fidelity U-Net Lite, a faster version of the proposed architecture, with 35% faster training, with 2 to 5% reduction in accuracy. We carry out extensive validation to show that the proposed models surpass traditional single-fidelity GNN models in their performance, thus providing feasible alternative for addressing computational and accuracy requirements where traditional high-fidelity simulations can be time-consuming.

GNN-based physics solver for time-independent PDEs

Physics-based deep learning frameworks have shown to be effective in accurately modeling the dynamics of complex physical systems with generalization capability across problem inputs. However, time-independent problems pose the challenge of requiring long-range exchange of information across the computational domain for obtaining accurate predictions. In the context of graph neural networks (GNNs), this calls for deeper networks, which, in turn, may compromise or slow down the training process. In this work, we present two GNN architectures to overcome this challenge - the Edge Augmented GNN and the Multi-GNN. We show that both these networks perform significantly better (by a factor of 1.5 to 2) than baseline methods when applied to time-independent solid mechanics problems. Furthermore, the proposed architectures generalize well to unseen domains, boundary conditions, and materials. Here, the treatment of variable domains is facilitated by a novel coordinate transformation that enables rotation and translation invariance. By broadening the range of problems that neural operators based on graph neural networks can tackle, this paper provides the groundwork for their application to complex scientific and industrial settings.

Robust Topology Optimization Using Variational Autoencoders

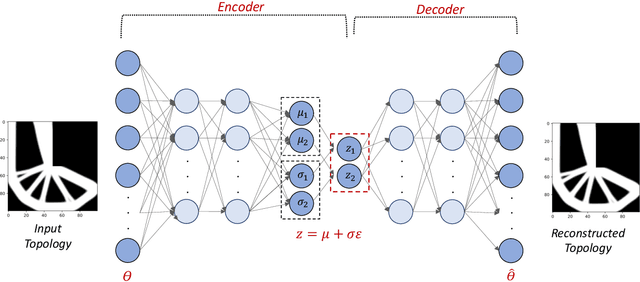
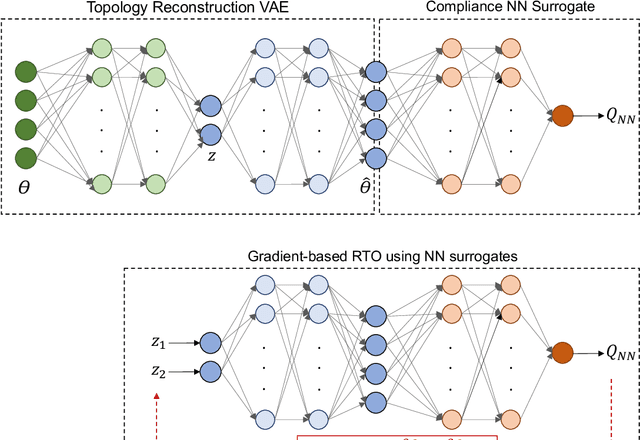
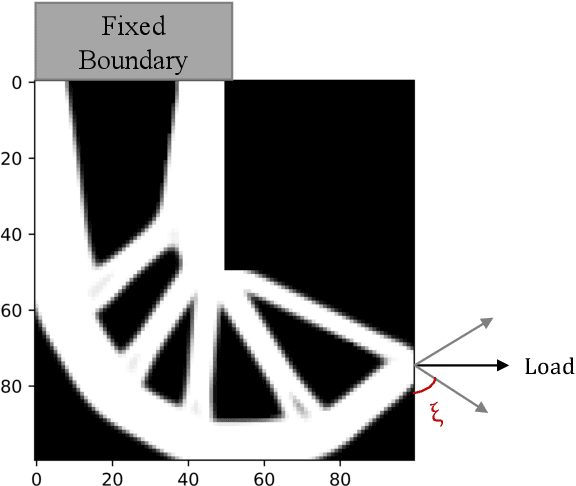
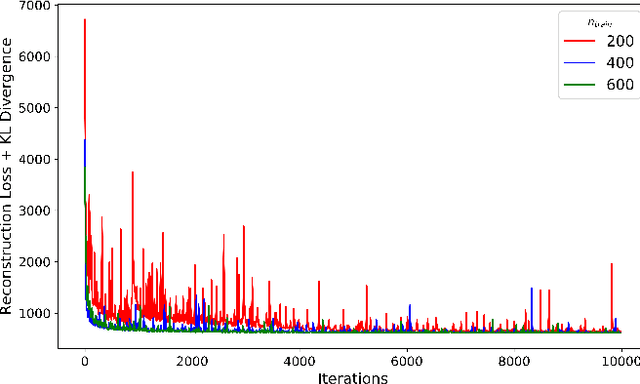
Topology Optimization is the process of finding the optimal arrangement of materials within a design domain by minimizing a cost function, subject to some performance constraints. Robust topology optimization (RTO) also incorporates the effect of input uncertainties and produces a design with the best average performance of the structure while reducing the response sensitivity to input uncertainties. It is computationally expensive to carry out RTO using finite element and Monte Carlo sampling. In this work, we use neural network surrogates to enable a faster solution approach via surrogate-based optimization and build a Variational Autoencoder (VAE) to transform the the high dimensional design space into a low dimensional one. Furthermore, finite element solvers will be replaced by a neural network surrogate. Also, to further facilitate the design exploration, we limit our search to a subspace, which consists of designs that are solutions to deterministic topology optimization problems under different realizations of input uncertainties. With these neural network approximations, a gradient-based optimization approach is formed to minimize the predicted objective function over the low dimensional design subspace. We demonstrate the effectiveness of the proposed approach on two compliance minimization problems and show that VAE performs well on learning the features of the design from minimal training data, and that converting the design space into a low dimensional latent space makes the problem computationally efficient. The resulting gradient-based optimization algorithm produces optimal designs with lower robust compliances than those observed in the training set.

Efficient training of physics-informed neural networks via importance sampling

Physics-Informed Neural Networks (PINNs) are a class of deep neural networks that are trained, using automatic differentiation, to compute the response of systems governed by partial differential equations (PDEs). The training of PINNs is simulation-free, and does not require any training dataset to be obtained from numerical PDE solvers. Instead, it only requires the physical problem description, including the governing laws of physics, domain geometry, initial/boundary conditions, and the material properties. This training usually involves solving a non-convex optimization problem using variants of the stochastic gradient descent method, with the gradient of the loss function approximated on a batch of collocation points, selected randomly in each iteration according to a uniform distribution. Despite the success of PINNs in accurately solving a wide variety of PDEs, the method still requires improvements in terms of computational efficiency. To this end, in this paper, we study the performance of an importance sampling approach for efficient training of PINNs. Using numerical examples together with theoretical evidences, we show that in each training iteration, sampling the collocation points according to a distribution proportional to the loss function will improve the convergence behavior of the PINNs training. Additionally, we show that providing a piecewise constant approximation to the loss function for faster importance sampling can further improve the training efficiency. This importance sampling approach is straightforward and easy to implement in the existing PINN codes, and also does not introduce any new hyperparameter to calibrate. The numerical examples include elasticity, diffusion and plane stress problems, through which we numerically verify the accuracy and efficiency of the importance sampling approach compared to the predominant uniform sampling approach.