Geometry-Informed Neural Operator Transformer

Machine-learning-based surrogate models offer significant computational efficiency and faster simulations compared to traditional numerical methods, especially for problems requiring repeated evaluations of partial differential equations. This work introduces the Geometry-Informed Neural Operator Transformer (GINOT), which integrates the transformer architecture with the neural operator framework to enable forward predictions for arbitrary geometries. GINOT encodes the surface points cloud of a geometry using a sampling and grouping mechanism combined with an attention mechanism, ensuring invariance to point order and padding while maintaining robustness to variations in point density. The geometry information is seamlessly integrated with query points in the solution decoder through the attention mechanism. The performance of GINOT is validated on multiple challenging datasets, showcasing its high accuracy and strong generalization capabilities for complex and arbitrary 2D and 3D geometries.

Multi-Class Traffic Assignment using Multi-View Heterogeneous Graph Attention Networks

Solving traffic assignment problem for large networks is computationally challenging when conventional optimization-based methods are used. In our research, we develop an innovative surrogate model for a traffic assignment when multi-class vehicles are involved. We do so by employing heterogeneous graph neural networks which use a multiple-view graph attention mechanism tailored to different vehicle classes, along with additional links connecting origin-destination pairs. We also integrate the node-based flow conservation law into the loss function. As a result, our model adheres to flow conservation while delivering highly accurate predictions for link flows and utilization ratios. Through numerical experiments conducted on urban transportation networks, we demonstrate that our model surpasses traditional neural network approaches in convergence speed and predictive accuracy in both user equilibrium and system optimal versions of traffic assignment.

PINN-FEM: A Hybrid Approach for Enforcing Dirichlet Boundary Conditions in Physics-Informed Neural Networks

Physics-Informed Neural Networks (PINNs) solve partial differential equations (PDEs) by embedding governing equations and boundary/initial conditions into the loss function. However, enforcing Dirichlet boundary conditions accurately remains challenging, often leading to soft enforcement that compromises convergence and reliability in complex domains. We propose a hybrid approach, PINN-FEM, which combines PINNs with finite element methods (FEM) to impose strong Dirichlet boundary conditions via domain decomposition. This method incorporates FEM-based representations near the boundary, ensuring exact enforcement without compromising convergence. Through six experiments of increasing complexity, PINN-FEM outperforms standard PINN models, showcasing superior accuracy and robustness. While distance functions and similar techniques have been proposed for boundary condition enforcement, they lack generality for real-world applications. PINN-FEM bridges this gap by leveraging FEM near boundaries, making it well-suited for industrial and scientific problems.

A Multi-Fidelity Graph U-Net Model for Accelerated Physics Simulations

Physics-based deep learning frameworks have shown to be effective in accurately modeling the dynamics of complex physical systems with generalization capability across problem inputs. Data-driven networks like GNN, Neural Operators have proved to be very effective in generalizing the model across unseen domain and resolutions. But one of the most critical issues in these data-based models is the computational cost of generating training datasets. Complex phenomena can only be captured accurately using deep networks with large training datasets. Furthermore, numerical error of training samples is propagated in the model errors, thus requiring the need for accurate data, i.e. FEM solutions on high-resolution meshes. Multi-fidelity methods offer a potential solution to reduce the training data requirements. To this end, we propose a novel GNN architecture, Multi-Fidelity U-Net, that utilizes the advantages of the multi-fidelity methods for enhancing the performance of the GNN model. The proposed architecture utilizes the capability of GNNs to manage complex geometries across different fidelity levels, while enabling flow of information between these levels for improved prediction accuracy for high-fidelity graphs. We show that the proposed approach performs significantly better in accuracy and data requirement and only requires training of a single network compared to other benchmark multi-fidelity approaches like transfer learning. We also present Multi-Fidelity U-Net Lite, a faster version of the proposed architecture, with 35% faster training, with 2 to 5% reduction in accuracy. We carry out extensive validation to show that the proposed models surpass traditional single-fidelity GNN models in their performance, thus providing feasible alternative for addressing computational and accuracy requirements where traditional high-fidelity simulations can be time-consuming.

Supply Chain Network Extraction and Entity Classification Leveraging Large Language Models

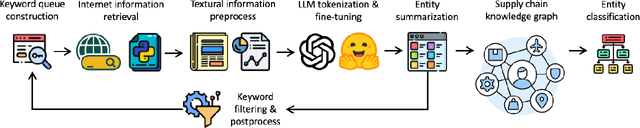
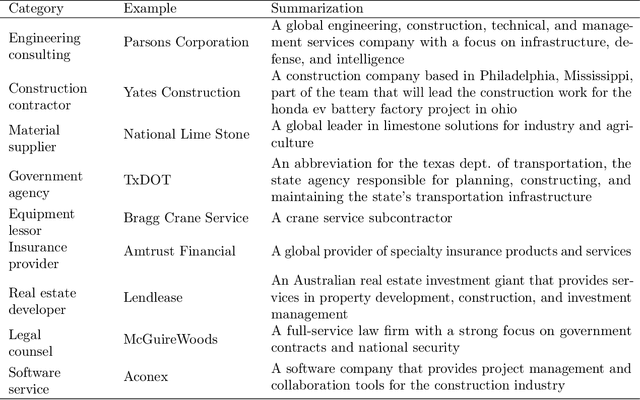
Supply chain networks are critical to the operational efficiency of industries, yet their increasing complexity presents significant challenges in mapping relationships and identifying the roles of various entities. Traditional methods for constructing supply chain networks rely heavily on structured datasets and manual data collection, limiting their scope and efficiency. In contrast, recent advancements in Natural Language Processing (NLP) and large language models (LLMs) offer new opportunities for discovering and analyzing supply chain networks using unstructured text data. This paper proposes a novel approach that leverages LLMs to extract and process raw textual information from publicly available sources to construct a comprehensive supply chain graph. We focus on the civil engineering sector as a case study, demonstrating how LLMs can uncover hidden relationships among companies, projects, and other entities. Additionally, we fine-tune an LLM to classify entities within the supply chain graph, providing detailed insights into their roles and relationships. The results show that domain-specific fine-tuning improves classification accuracy, highlighting the potential of LLMs for industry-specific supply chain analysis. Our contributions include the development of a supply chain graph for the civil engineering sector, as well as a fine-tuned LLM model that enhances entity classification and understanding of supply chain networks.

Heterogeneous Graph Sequence Neural Networks for Dynamic Traffic Assignment

Traffic assignment and traffic flow prediction provide critical insights for urban planning, traffic management, and the development of intelligent transportation systems. An efficient model for calculating traffic flows over the entire transportation network could provide a more detailed and realistic understanding of traffic dynamics. However, existing traffic prediction approaches, such as those utilizing graph neural networks, are typically limited to locations where sensors are deployed and cannot predict traffic flows beyond sensor locations. To alleviate this limitation, inspired by fundamental relationship that exists between link flows and the origin-destination (OD) travel demands, we proposed the Heterogeneous Spatio-Temporal Graph Sequence Network (HSTGSN). HSTGSN exploits dependency between origin and destination nodes, even when it is long-range, and learns implicit vehicle route choices under different origin-destination demands. This model is based on a heterogeneous graph which consists of road links, OD links (virtual links connecting origins and destinations) and a spatio-temporal graph encoder-decoder that captures the spatio-temporal relationship between OD demands and flow distribution. We will show how the graph encoder-decoder is able to recover the incomplete information in the OD demand, by using node embedding from the graph decoder to predict the temporal changes in flow distribution. Using extensive experimental studies on real-world networks with complete/incomplete OD demands, we demonstrate that our method can not only capture the implicit spatio-temporal relationship between link traffic flows and OD demands but also achieve accurate prediction performance and generalization capability.

Physics-Informed Geometry-Aware Neural Operator

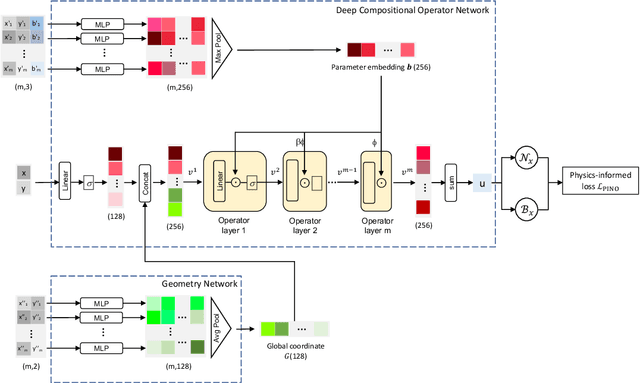
Engineering design problems often involve solving parametric Partial Differential Equations (PDEs) under variable PDE parameters and domain geometry. Recently, neural operators have shown promise in learning PDE operators and quickly predicting the PDE solutions. However, training these neural operators typically requires large datasets, the acquisition of which can be prohibitively expensive. To overcome this, physics-informed training offers an alternative way of building neural operators, eliminating the high computational costs associated with Finite Element generation of training data. Nevertheless, current physics-informed neural operators struggle with limitations, either in handling varying domain geometries or varying PDE parameters. In this research, we introduce a novel method, the Physics-Informed Geometry-Aware Neural Operator (PI-GANO), designed to simultaneously generalize across both PDE parameters and domain geometries. We adopt a geometry encoder to capture the domain geometry features, and design a novel pipeline to integrate this component within the existing DCON architecture. Numerical results demonstrate the accuracy and efficiency of the proposed method.

Physics-informed Mesh-independent Deep Compositional Operator Network

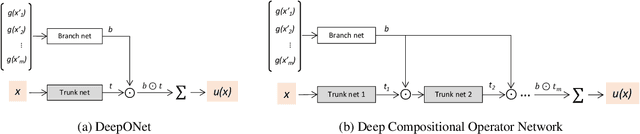
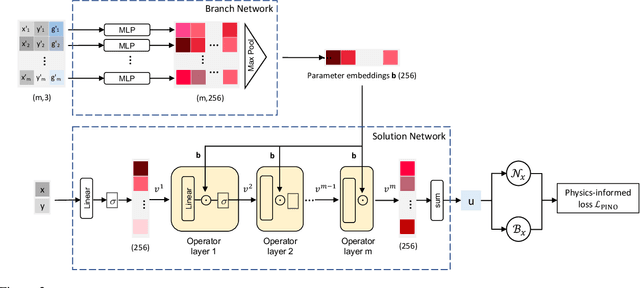
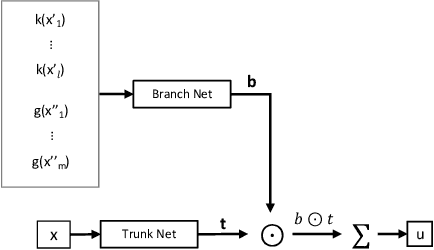
Solving parametric Partial Differential Equations (PDEs) for a broad range of parameters is a critical challenge in scientific computing. To this end, neural operators, which learn mappings from parameters to solutions, have been successfully used. However, the training of neural operators typically demands large training datasets, the acquisition of which can be prohibitively expensive. To address this challenge, physics-informed training can offer a cost-effective strategy. However, current physics-informed neural operators face limitations, either in handling irregular domain shapes or in generalization to various discretizations of PDE parameters with variable mesh sizes. In this research, we introduce a novel physics-informed model architecture which can generalize to parameter discretizations of variable size and irregular domain shapes. Particularly, inspired by deep operator neural networks, our model involves a discretization-independent learning of parameter embedding repeatedly, and this parameter embedding is integrated with the response embeddings through multiple compositional layers, for more expressivity. Numerical results demonstrate the accuracy and efficiency of the proposed method.

Heterogeneous Graph Neural Networks for Data-driven Traffic Assignment

The traffic assignment problem is one of the significant components of traffic flow analysis for which various solution approaches have been proposed. However, deploying these approaches for large-scale networks poses significant challenges. In this paper, we leverage the power of heterogeneous graph neural networks to propose a novel data-driven approach for traffic assignment and traffic flow learning. The proposed model is capable of capturing spatial traffic patterns across different links, yielding highly accurate results. We present numerical experiments on urban transportation networks and show that the proposed heterogeneous graph neural network model outperforms other conventional neural network models in terms of convergence rate, training loss, and prediction accuracy. Notably, the proposed heterogeneous graph neural network model can also be generalized to different network topologies. This approach offers a promising solution for complex traffic flow analysis and prediction, enhancing our understanding and management of a wide range of transportation systems.

Attention-based Spatial-Temporal Graph Neural ODE for Traffic Prediction

Traffic forecasting is an important issue in intelligent traffic systems (ITS). Graph neural networks (GNNs) are effective deep learning models to capture the complex spatio-temporal dependency of traffic data, achieving ideal prediction performance. In this paper, we propose attention-based graph neural ODE (ASTGODE) that explicitly learns the dynamics of the traffic system, which makes the prediction of our machine learning model more explainable. Our model aggregates traffic patterns of different periods and has satisfactory performance on two real-world traffic data sets. The results show that our model achieves the highest accuracy of the root mean square error metric among all the existing GNN models in our experiments.