Univariate Conditional Variational Autoencoder for Morphogenic Patterns Design in Frontal Polymerization-Based Manufacturing

Rapid reaction-thermal diffusion during frontal polymerization (FP) with variations in initial and boundary conditions destabilizes the planar mode of front propagation, leading to spatially varying complex hierarchical patterns in polymeric materials. Although modern reaction-diffusion models can predict the patterns resulting from unstable FP, the inverse design of patterns, which aims to retrieve process conditions that produce a desired pattern, remains an open challenge due to the nonunique and nonintuitive mapping between process conditions and patterns. In this work, we propose a novel probabilistic generative model named univariate conditional variational autoencoder (UcVAE) for the inverse design of hierarchical patterns in FP-based manufacturing. Unlike the cVAE, which encodes both the design space and the design target, the UcVAE encodes only the design space. In the encoder of the UcVAE, the number of training parameters is significantly reduced compared to the cVAE, resulting in a shorter training time while maintaining comparable performance. Given desired pattern images, the trained UcVAE can generate multiple process condition solutions that produce high-fidelity hierarchical patterns.

Virtual Sensing for Real-Time Degradation Monitoring of Nuclear Systems: Leveraging DeepONet for Enhanced Sensing Coverage for Digital Twin-Enabling Technology

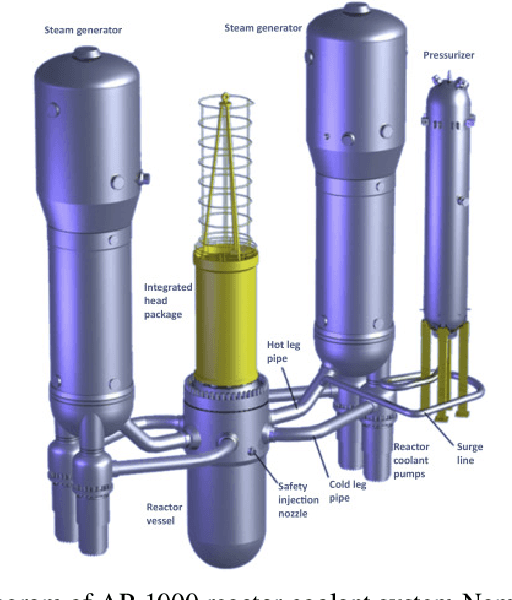
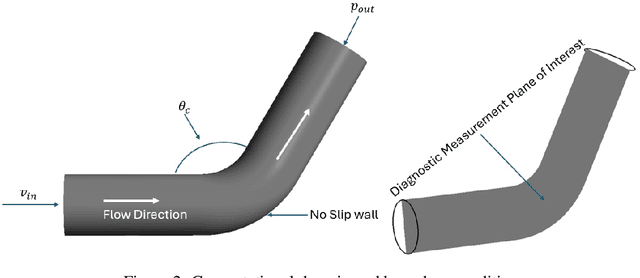
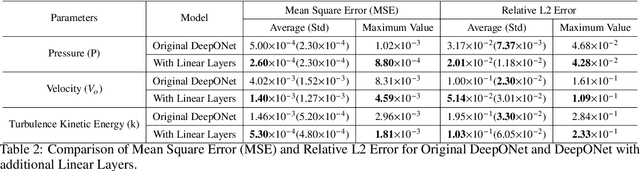
Effective real-time monitoring technique is crucial for detecting material degradation and maintaining the structural integrity of nuclear systems to ensure both safety and operational efficiency. Traditional physical sensor systems face limitations such as installation challenges, high costs, and difficulties in measuring critical parameters in hard-to-reach or harsh environments, often resulting in incomplete data coverage. Machine learning-driven virtual sensors offer a promising solution by enhancing physical sensor capabilities to monitor critical degradation indicators like pressure, velocity, and turbulence. However, conventional machine learning models struggle with real-time monitoring due to the high-dimensional nature of reactor data and the need for frequent retraining. This paper explores the use of Deep Operator Networks (DeepONet) within a digital twin (DT) framework to predict key thermal-hydraulic parameters in the hot leg of an AP-1000 Pressurized Water Reactor (PWR). In this study, DeepONet is trained with different operational conditions, which relaxes the requirement of continuous retraining, making it suitable for online and real-time prediction components for DT. Our results show that DeepONet achieves accurate predictions with low mean squared error and relative L2 error and can make predictions on unknown data 160,000 times faster than traditional finite element (FE) simulations. This speed and accuracy make DeepONet a powerful tool for tracking conditions that contribute to material degradation in real-time, enhancing reactor safety and longevity.

Nonlinear Inverse Design of Mechanical Multi-Material Metamaterials Enabled by Video Denoising Diffusion and Structure Identifier

Metamaterials, synthetic materials with customized properties, have emerged as a promising field due to advancements in additive manufacturing. These materials derive unique mechanical properties from their internal lattice structures, which are often composed of multiple materials that repeat geometric patterns. While traditional inverse design approaches have shown potential, they struggle to map nonlinear material behavior to multiple possible structural configurations. This paper presents a novel framework leveraging video diffusion models, a type of generative artificial Intelligence (AI), for inverse multi-material design based on nonlinear stress-strain responses. Our approach consists of two key components: (1) a fields generator using a video diffusion model to create solution fields based on target nonlinear stress-strain responses, and (2) a structure identifier employing two UNet models to determine the corresponding multi-material 2D design. By incorporating multiple materials, plasticity, and large deformation, our innovative design method allows for enhanced control over the highly nonlinear mechanical behavior of metamaterials commonly seen in real-world applications. It offers a promising solution for generating next-generation metamaterials with finely tuned mechanical characteristics.

A deep learning energy method for hyperelasticity and viscoelasticity

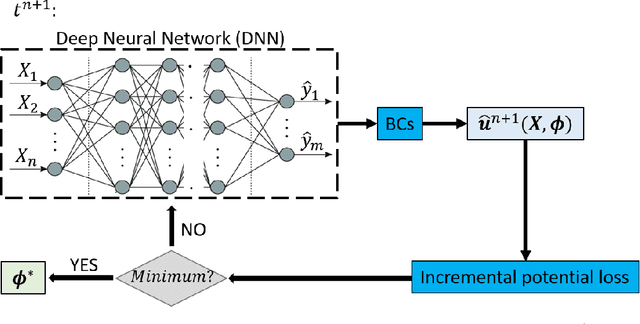
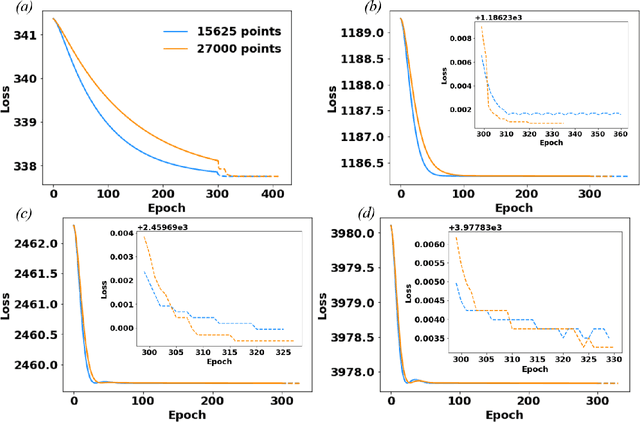
The potential energy formulation and deep learning are merged to solve partial differential equations governing the deformation in hyperelastic and viscoelastic materials. The presented deep energy method (DEM) is self-contained and meshfree. It can accurately capture the three-dimensional (3D) mechanical response without requiring any time-consuming training data generation by classical numerical methods such as the finite element method. Once the model is appropriately trained, the response can be attained almost instantly at any point in the physical domain, given its spatial coordinates. Therefore, the deep energy method is potentially a promising standalone method for solving partial differential equations describing the mechanical deformation of materials or structural systems and other physical phenomena.

Deep learning collocation method for solid mechanics: Linear elasticity, hyperelasticity, and plasticity as examples

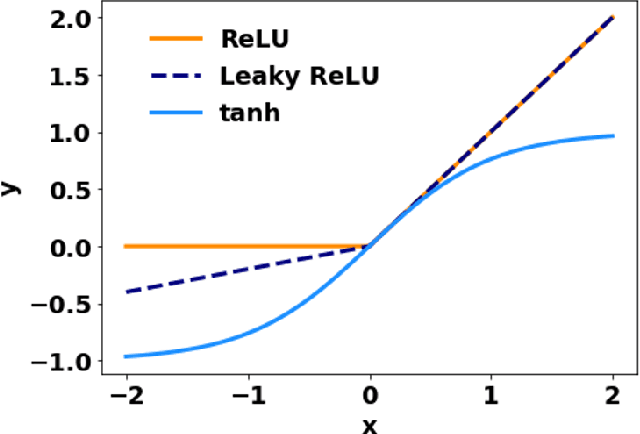
Deep learning and the collocation method are merged and used to solve partial differential equations describing structures' deformation. We have considered different types of materials: linear elasticity, hyperelasticity (neo-Hookean) with large deformation, and von Mises plasticity with isotropic and kinematic hardening. The performance of this deep collocation method (DCM) depends on the architecture of the neural network and the corresponding hyperparameters. The presented DCM is meshfree and avoids any spatial discretization, which is usually needed for the finite element method (FEM). We show that the DCM can capture the response qualitatively and quantitatively, without the need for any data generation using other numerical methods such as the FEM. Data generation usually is the main bottleneck in most data-driven models. The deep learning model is trained to learn the model's parameters yielding accurate approximate solutions. Once the model is properly trained, solutions can be obtained almost instantly at any point in the domain, given its spatial coordinates. Therefore, the deep collocation method is potentially a promising standalone technique to solve partial differential equations involved in the deformation of materials and structural systems as well as other physical phenomena.

Convergence of Artificial Intelligence and High Performance Computing on NSF-supported Cyberinfrastructure

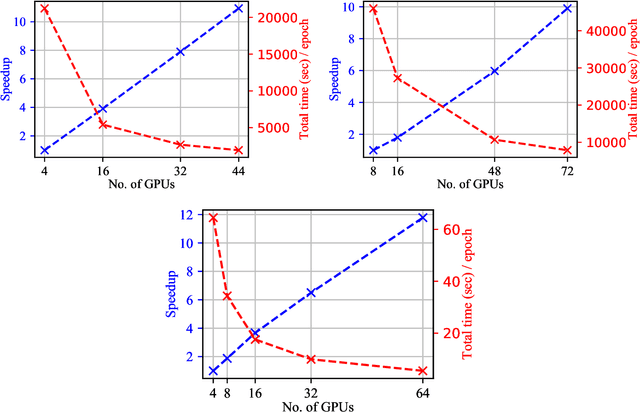
Significant investments to upgrade or construct large-scale scientific facilities demand commensurate investments in R&D to design algorithms and computing approaches to enable scientific and engineering breakthroughs in the big data era. The remarkable success of Artificial Intelligence (AI) algorithms to turn big-data challenges in industry and technology into transformational digital solutions that drive a multi-billion dollar industry, which play an ever increasing role shaping human social patterns, has promoted AI as the most sought after signal processing tool in big-data research. As AI continues to evolve into a computing tool endowed with statistical and mathematical rigor, and which encodes domain expertise to inform and inspire AI architectures and optimization algorithms, it has become apparent that single-GPU solutions for training, validation, and testing are no longer sufficient. This realization has been driving the confluence of AI and high performance computing (HPC) to reduce time-to-insight and to produce robust, reliable, trustworthy, and computationally efficient AI solutions. In this white paper, we present a summary of recent developments in this field, and discuss avenues to accelerate and streamline the use of HPC platforms to design accelerated AI algorithms.

Machine learning accelerated topology optimization of nonlinear structures

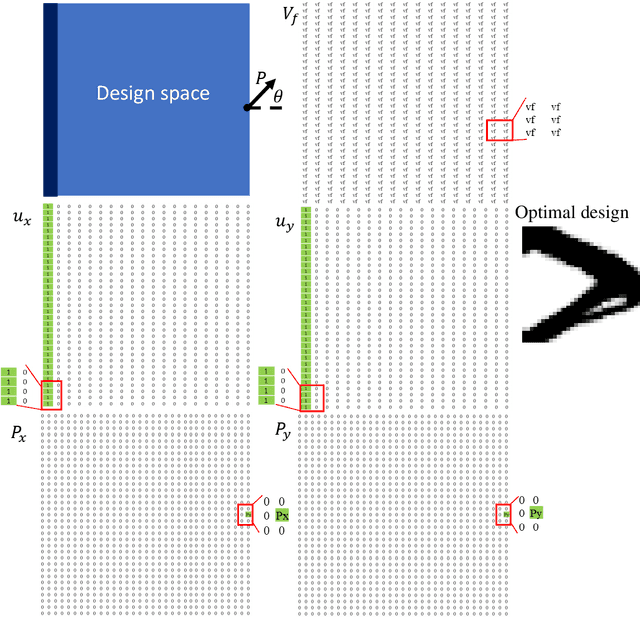
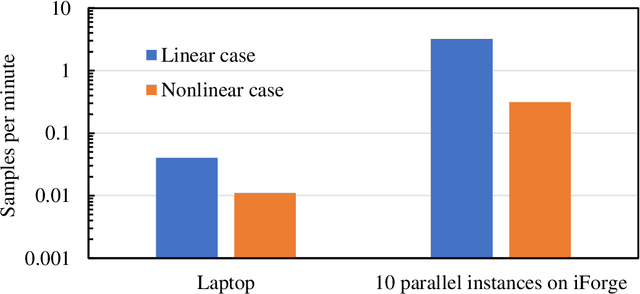
The field of optimal design of linear elastic structures has seen many exciting successes that resulted in new architected materials and designs. With the availability of cloud computing, including high-performance computing, machine learning, and simulation, searching for optimal nonlinear structures is now within reach. In this study, we develop two convolutional neural network models to predict optimized designs for a given set of boundary conditions, loads, and volume constraints. The first convolutional neural network model is for the case of materials with a linear elastic response while the second developed model is for hyperelastic response where material and geometric nonlinearities are involved. For the nonlinear elastic case, the neo-Hookean model is utilized. For this purpose, we generate datasets, composed of the optimized designs paired with the corresponding boundary conditions, loads, and constraints, using topology optimization framework to train and validate both models. The developed models are capable of accurately predicting the optimized designs without requiring an iterative scheme and with negligible computational time. The suggested pipeline can be generalized to other nonlinear mechanics scenarios and design domains.