Machine learning accelerated topology optimization of nonlinear structures

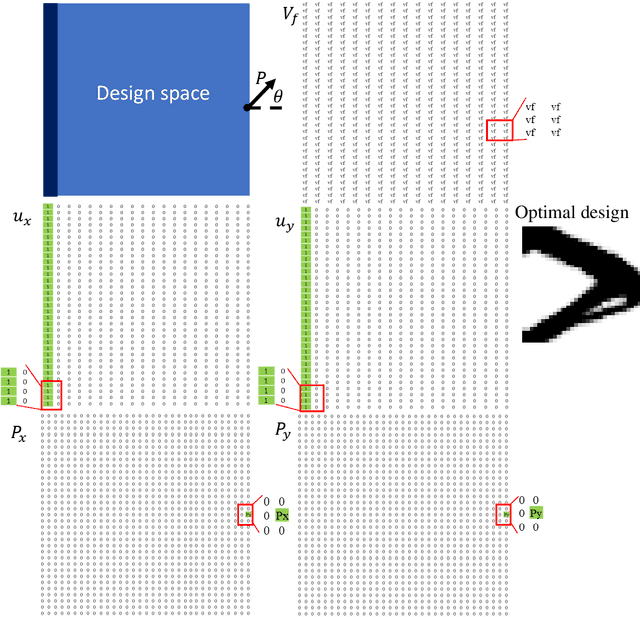
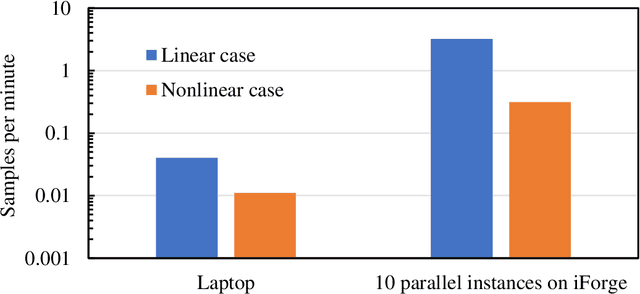
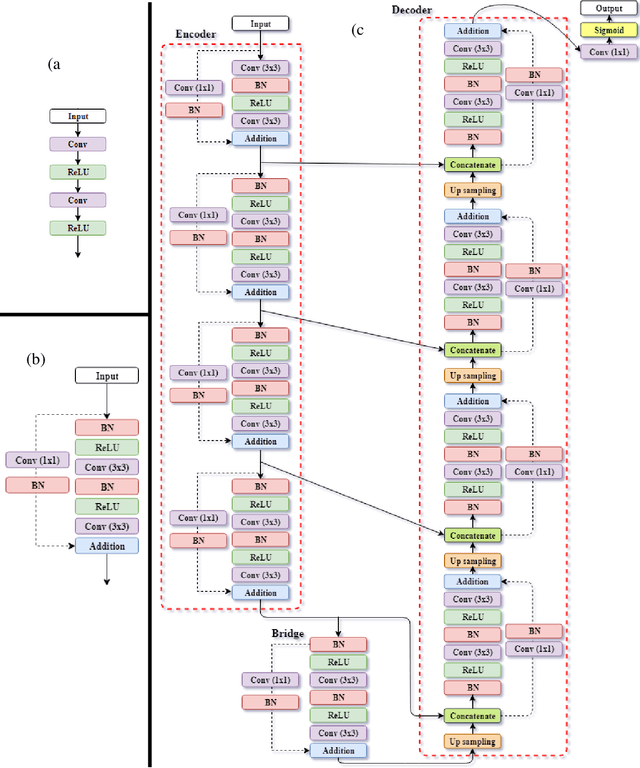
The field of optimal design of linear elastic structures has seen many exciting successes that resulted in new architected materials and designs. With the availability of cloud computing, including high-performance computing, machine learning, and simulation, searching for optimal nonlinear structures is now within reach. In this study, we develop two convolutional neural network models to predict optimized designs for a given set of boundary conditions, loads, and volume constraints. The first convolutional neural network model is for the case of materials with a linear elastic response while the second developed model is for hyperelastic response where material and geometric nonlinearities are involved. For the nonlinear elastic case, the neo-Hookean model is utilized. For this purpose, we generate datasets, composed of the optimized designs paired with the corresponding boundary conditions, loads, and constraints, using topology optimization framework to train and validate both models. The developed models are capable of accurately predicting the optimized designs without requiring an iterative scheme and with negligible computational time. The suggested pipeline can be generalized to other nonlinear mechanics scenarios and design domains.