A deep learning energy method for hyperelasticity and viscoelasticity

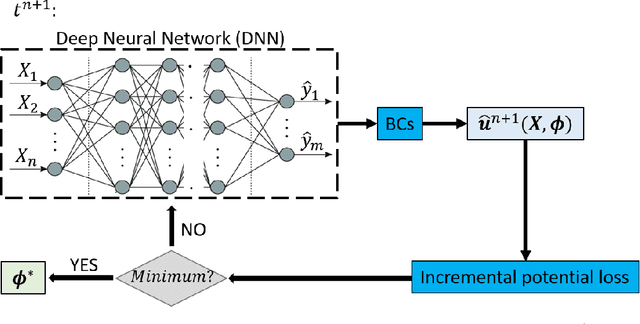
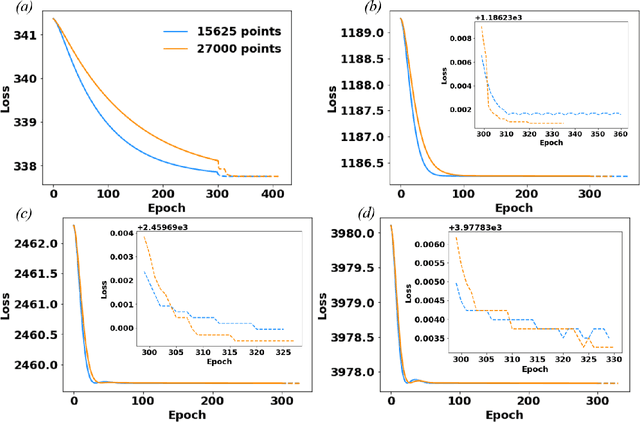
The potential energy formulation and deep learning are merged to solve partial differential equations governing the deformation in hyperelastic and viscoelastic materials. The presented deep energy method (DEM) is self-contained and meshfree. It can accurately capture the three-dimensional (3D) mechanical response without requiring any time-consuming training data generation by classical numerical methods such as the finite element method. Once the model is appropriately trained, the response can be attained almost instantly at any point in the physical domain, given its spatial coordinates. Therefore, the deep energy method is potentially a promising standalone method for solving partial differential equations describing the mechanical deformation of materials or structural systems and other physical phenomena.

Machine learning accelerated topology optimization of nonlinear structures

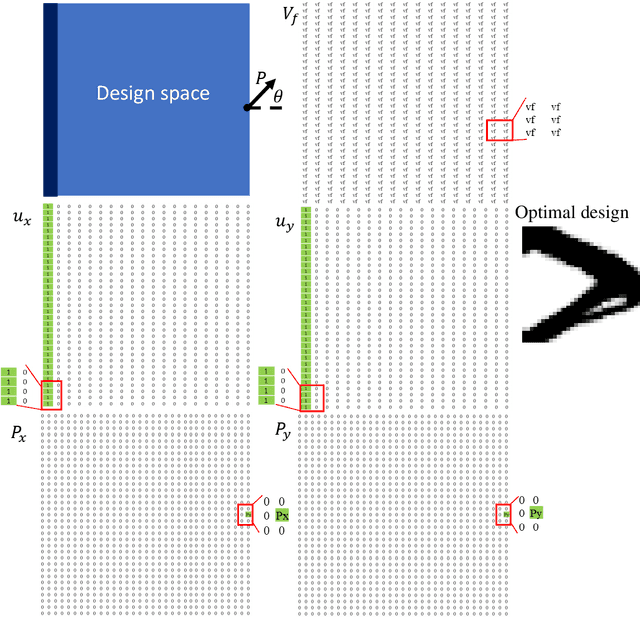
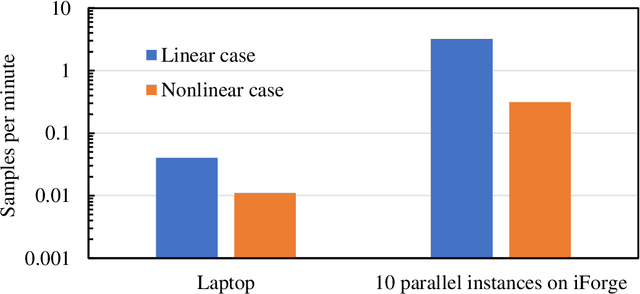
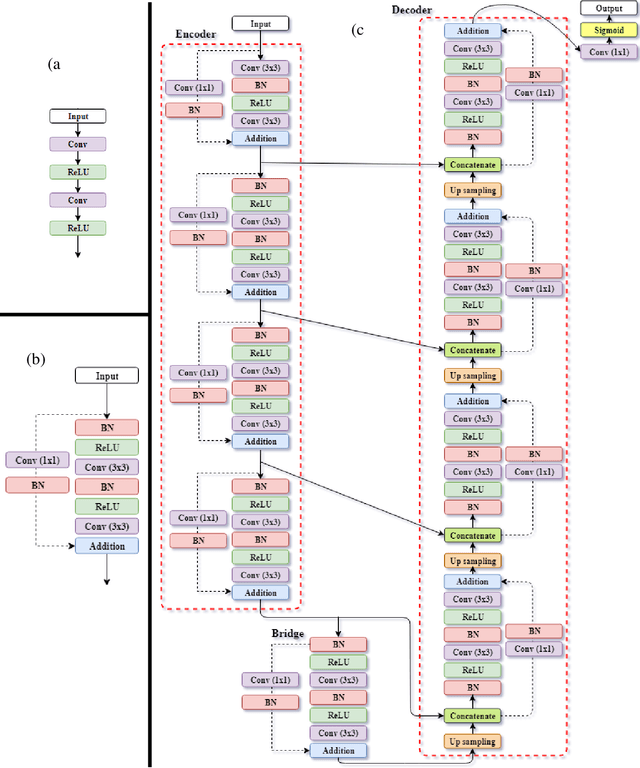
The field of optimal design of linear elastic structures has seen many exciting successes that resulted in new architected materials and designs. With the availability of cloud computing, including high-performance computing, machine learning, and simulation, searching for optimal nonlinear structures is now within reach. In this study, we develop two convolutional neural network models to predict optimized designs for a given set of boundary conditions, loads, and volume constraints. The first convolutional neural network model is for the case of materials with a linear elastic response while the second developed model is for hyperelastic response where material and geometric nonlinearities are involved. For the nonlinear elastic case, the neo-Hookean model is utilized. For this purpose, we generate datasets, composed of the optimized designs paired with the corresponding boundary conditions, loads, and constraints, using topology optimization framework to train and validate both models. The developed models are capable of accurately predicting the optimized designs without requiring an iterative scheme and with negligible computational time. The suggested pipeline can be generalized to other nonlinear mechanics scenarios and design domains.

Prediction and optimization of mechanical properties of composites using convolutional neural networks

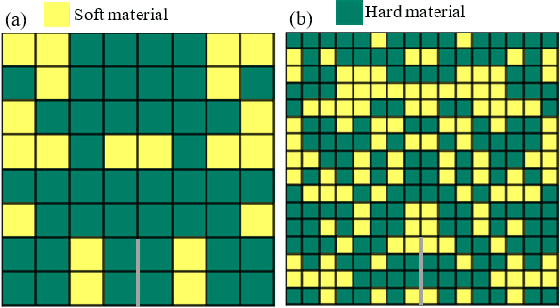
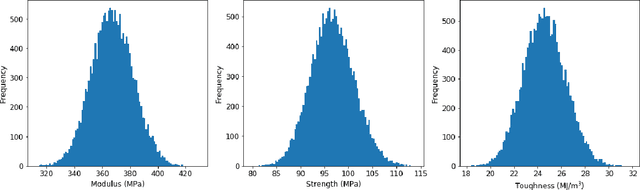
In this paper, we develop a convolutional neural network model to predict the mechanical properties of a two-dimensional checkerboard composite quantitatively. The checkerboard composite possesses two phases, one phase is soft and ductile while the other is stiff and brittle. The ground-truth data used in the training process are obtained from finite element analyses under the assumption of plane stress. Monte Carlo simulations and central limit theorem are used to find the size of the dataset needed. Once the training process is completed, the developed model is validated using data unseen during training. The developed neural network model captures the stiffness, strength, and toughness of checkerboard composites with high accuracy. Also, we integrate the developed model with a genetic algorithm (GA) optimizer to identify the optimal microstructural designs. The genetic algorithm optimizer adopted here has several operators, selection, crossover, mutation, and elitism. The optimizer converges to configurations with highly enhanced properties. For the case of the modulus and starting from randomly-initialized generation, the GA optimizer converges to the global maximum which involves no soft elements. Also, the GA optimizers, when used to maximize strength and toughness, tend towards having soft elements in the region next to the crack tip.