Safe and Reliable Training of Learning-Based Aerospace Controllers

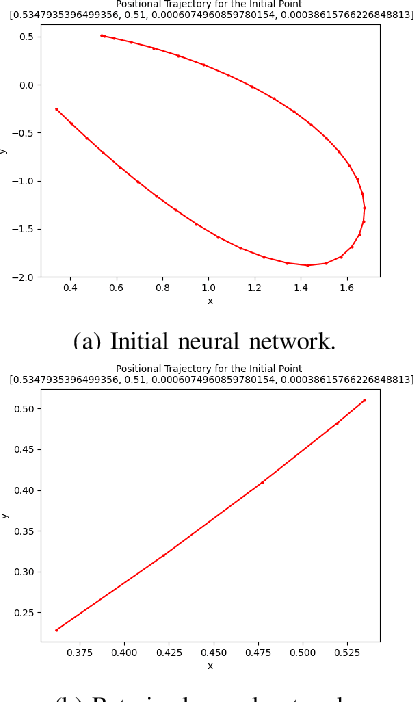
In recent years, deep reinforcement learning (DRL) approaches have generated highly successful controllers for a myriad of complex domains. However, the opaque nature of these models limits their applicability in aerospace systems and safety-critical domains, in which a single mistake can have dire consequences. In this paper, we present novel advancements in both the training and verification of DRL controllers, which can help ensure their safe behavior. We showcase a design-for-verification approach utilizing k-induction and demonstrate its use in verifying liveness properties. In addition, we also give a brief overview of neural Lyapunov Barrier certificates and summarize their capabilities on a case study. Finally, we describe several other novel reachability-based approaches which, despite failing to provide guarantees of interest, could be effective for verification of other DRL systems, and could be of further interest to the community.

Prediction and optimization of mechanical properties of composites using convolutional neural networks

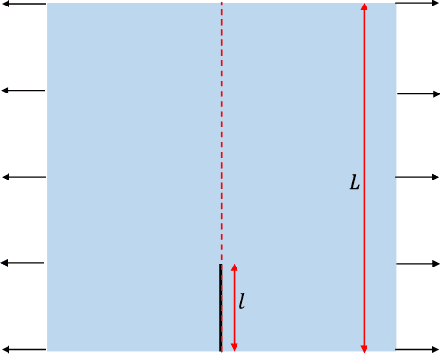
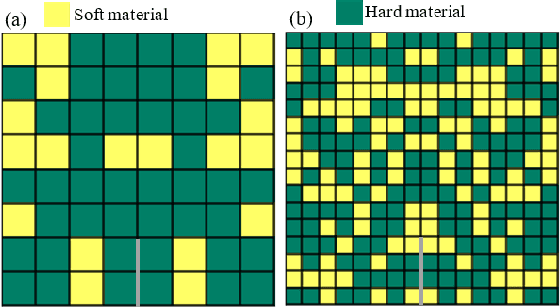
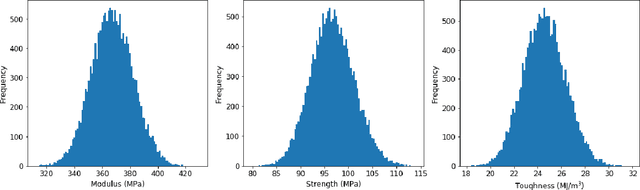
In this paper, we develop a convolutional neural network model to predict the mechanical properties of a two-dimensional checkerboard composite quantitatively. The checkerboard composite possesses two phases, one phase is soft and ductile while the other is stiff and brittle. The ground-truth data used in the training process are obtained from finite element analyses under the assumption of plane stress. Monte Carlo simulations and central limit theorem are used to find the size of the dataset needed. Once the training process is completed, the developed model is validated using data unseen during training. The developed neural network model captures the stiffness, strength, and toughness of checkerboard composites with high accuracy. Also, we integrate the developed model with a genetic algorithm (GA) optimizer to identify the optimal microstructural designs. The genetic algorithm optimizer adopted here has several operators, selection, crossover, mutation, and elitism. The optimizer converges to configurations with highly enhanced properties. For the case of the modulus and starting from randomly-initialized generation, the GA optimizer converges to the global maximum which involves no soft elements. Also, the GA optimizers, when used to maximize strength and toughness, tend towards having soft elements in the region next to the crack tip.