The 6th International Verification of Neural Networks Competition (VNN-COMP 2025): Summary and Results

This report summarizes the 6th International Verification of Neural Networks Competition (VNN-COMP 2025), held as a part of the 8th International Symposium on AI Verification (SAIV), that was collocated with the 37th International Conference on Computer-Aided Verification (CAV). VNN-COMP is held annually to facilitate the fair and objective comparison of state-of-the-art neural network verification tools, encourage the standardization of tool interfaces, and bring together the neural network verification community. To this end, standardized formats for networks (ONNX) and specification (VNN-LIB) were defined, tools were evaluated on equal-cost hardware (using an automatic evaluation pipeline based on AWS instances), and tool parameters were chosen by the participants before the final test sets were made public. In the 2025 iteration, 8 teams participated on a diverse set of 16 regular and 9 extended benchmarks. This report summarizes the rules, benchmarks, participating tools, results, and lessons learned from this iteration of this competition.

Proof Minimization in Neural Network Verification

The widespread adoption of deep neural networks (DNNs) requires efficient techniques for verifying their safety. DNN verifiers are complex tools, which might contain bugs that could compromise their soundness and undermine the reliability of the verification process. This concern can be mitigated using proofs: artifacts that are checkable by an external and reliable proof checker, and which attest to the correctness of the verification process. However, such proofs tend to be extremely large, limiting their use in many scenarios. In this work, we address this problem by minimizing proofs of unsatisfiability produced by DNN verifiers. We present algorithms that remove facts which were learned during the verification process, but which are unnecessary for the proof itself. Conceptually, our method analyzes the dependencies among facts used to deduce UNSAT, and removes facts that did not contribute. We then further minimize the proof by eliminating remaining unnecessary dependencies, using two alternative procedures. We implemented our algorithms on top of a proof producing DNN verifier, and evaluated them across several benchmarks. Our results show that our best-performing algorithm reduces proof size by 37%-82% and proof checking time by 30%-88%, while introducing a runtime overhead of 7%-20% to the verification process itself.

The Tool Decathlon: Benchmarking Language Agents for Diverse, Realistic, and Long-Horizon Task Execution

Real-world language agents must handle complex, multi-step workflows across diverse Apps. For instance, an agent may manage emails by coordinating with calendars and file systems, or monitor a production database to detect anomalies and generate reports following an operating manual. However, existing language agent benchmarks often focus on narrow domains or simplified tasks that lack the diversity, realism, and long-horizon complexity required to evaluate agents' real-world performance. To address this gap, we introduce the Tool Decathlon (dubbed as Toolathlon), a benchmark for language agents offering diverse Apps and tools, realistic environment setup, and reliable execution-based evaluation. Toolathlon spans 32 software applications and 604 tools, ranging from everyday platforms such as Google Calendar and Notion to professional ones like WooCommerce, Kubernetes, and BigQuery. Most of the tools are based on a high-quality set of Model Context Protocol (MCP) servers that we may have revised or implemented ourselves. Unlike prior works, which primarily ensure functional realism but offer limited environment state diversity, we provide realistic initial environment states from real software, such as Canvas courses with dozens of students or real financial spreadsheets. This benchmark includes 108 manually sourced or crafted tasks in total, requiring interacting with multiple Apps over around 20 turns on average to complete. Each task is strictly verifiable through dedicated evaluation scripts. Comprehensive evaluation of SOTA models highlights their significant shortcomings: the best-performing model, Claude-4.5-Sonnet, achieves only a 38.6% success rate with 20.2 tool calling turns on average, while the top open-weights model DeepSeek-V3.2-Exp reaches 20.1%. We expect Toolathlon to drive the development of more capable language agents for real-world, long-horizon task execution.

Model-Task Alignment Drives Distinct RL Outcomes

Recent advances in applying reinforcement learning (RL) to large language models (LLMs) have led to substantial progress. In particular, a series of remarkable yet often counterintuitive phenomena have been reported in LLMs, exhibiting patterns not typically observed in traditional RL settings. For example, notable claims include that a single training example can match the performance achieved with an entire dataset, that the reward signal does not need to be very accurate, and that training solely with negative samples can match or even surpass sophisticated reward-based methods. However, the precise conditions under which these observations hold - and, critically, when they fail - remain unclear. In this work, we identify a key factor that differentiates RL observations: whether the pretrained model already exhibits strong Model-Task Alignment, as measured by pass@k accuracy on the evaluated task. Through a systematic and comprehensive examination of a series of counterintuitive claims, supported by rigorous experimental validation across different model architectures and task domains, our findings show that while standard RL training remains consistently robust across settings, many of these counterintuitive results arise only when the model and task already exhibit strong model-task alignment. In contrast, these techniques fail to drive substantial learning in more challenging regimes, where standard RL methods remain effective.

Abstraction-Based Proof Production in Formal Verification of Neural Networks

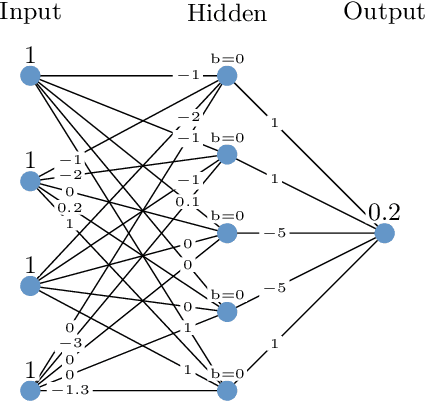
Modern verification tools for deep neural networks (DNNs) increasingly rely on abstraction to scale to realistic architectures. In parallel, proof production is becoming a critical requirement for increasing the reliability of DNN verification results. However, current proofproducing verifiers do not support abstraction-based reasoning, creating a gap between scalability and provable guarantees. We address this gap by introducing a novel framework for proof-producing abstraction-based DNN verification. Our approach modularly separates the verification task into two components: (i) proving the correctness of an abstract network, and (ii) proving the soundness of the abstraction with respect to the original DNN. The former can be handled by existing proof-producing verifiers, whereas we propose the first method for generating formal proofs for the latter. This preliminary work aims to enable scalable and trustworthy verification by supporting common abstraction techniques within a formal proof framework.

Proof-Driven Clause Learning in Neural Network Verification

The widespread adoption of deep neural networks (DNNs) requires efficient techniques for safety verification. Existing methods struggle to scale to real-world DNNs, and tremendous efforts are being put into improving their scalability. In this work, we propose an approach for improving the scalability of DNN verifiers using Conflict-Driven Clause Learning (CDCL) -- an approach that has proven highly successful in SAT and SMT solving. We present a novel algorithm for deriving conflict clauses using UNSAT proofs, and propose several optimizations for expediting it. Our approach allows a modular integration of SAT solvers and DNN verifiers, and we implement it on top of an interface designed for this purpose. The evaluation of our implementation over several benchmarks suggests a 2X--3X improvement over a similar approach, with specific cases outperforming the state of the art.

Neural Network Verification is a Programming Language Challenge

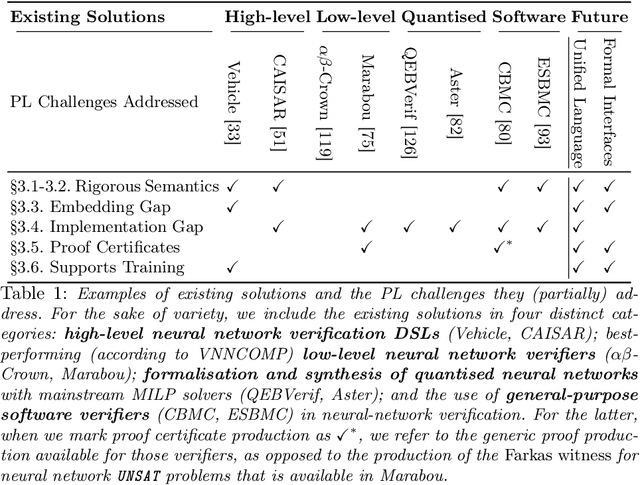
Neural network verification is a new and rapidly developing field of research. So far, the main priority has been establishing efficient verification algorithms and tools, while proper support from the programming language perspective has been considered secondary or unimportant. Yet, there is mounting evidence that insights from the programming language community may make a difference in the future development of this domain. In this paper, we formulate neural network verification challenges as programming language challenges and suggest possible future solutions.

The Fifth International Verification of Neural Networks Competition (VNN-COMP 2024): Summary and Results

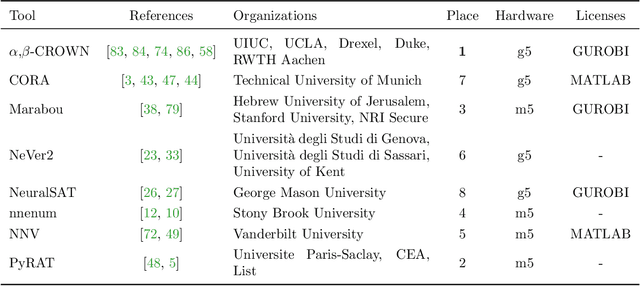
This report summarizes the 5th International Verification of Neural Networks Competition (VNN-COMP 2024), held as a part of the 7th International Symposium on AI Verification (SAIV), that was collocated with the 36th International Conference on Computer-Aided Verification (CAV). VNN-COMP is held annually to facilitate the fair and objective comparison of state-of-the-art neural network verification tools, encourage the standardization of tool interfaces, and bring together the neural network verification community. To this end, standardized formats for networks (ONNX) and specification (VNN-LIB) were defined, tools were evaluated on equal-cost hardware (using an automatic evaluation pipeline based on AWS instances), and tool parameters were chosen by the participants before the final test sets were made public. In the 2024 iteration, 8 teams participated on a diverse set of 12 regular and 8 extended benchmarks. This report summarizes the rules, benchmarks, participating tools, results, and lessons learned from this iteration of this competition.

USM: Unbiased Survey Modeling for Limiting Negative User Experiences in Recommendation Systems

Negative feedback signals are crucial to guardrail content recommendations and improve user experience. When these signals are effectively integrated into recommendation systems, they play a vital role in preventing the promotion of harmful or undesirable content, thereby contributing to a healthier online environment. However, the challenges associated with negative signals are noteworthy. Due to the limited visibility of options for users to express negative feedback, these signals are often sparse compared to positive signals. This imbalance can lead to a skewed understanding of user preferences, resulting in recommendations that prioritize short-term engagement over long-term satisfaction. Moreover, an over-reliance on positive signals can create a filter bubble, where users are continuously exposed to content that aligns with their immediate preferences but may not be beneficial in the long run. This scenario can ultimately lead to user attrition as audiences become disillusioned with the quality of the content provided. Additionally, existing user signals frequently fail to meet specific customized requirements, such as understanding the underlying reasons for a user's likes or dislikes regarding a video. This lack of granularity hinders our ability to tailor content recommendations effectively, as we cannot identify the particular attributes of content that resonate with individual users.

Better Verified Explanations with Applications to Incorrectness and Out-of-Distribution Detection

Building on VeriX (Verified eXplainability, arXiv:2212.01051), a system for producing optimal verified explanations for machine learning model outputs, we present VeriX+, which significantly improves both the size and the generation time of verified explanations. We introduce a bound propagation-based sensitivity technique to improve the size, and a binary search-based traversal with confidence ranking for improving time -- the two techniques are orthogonal and can be used independently or together. We also show how to adapt the QuickXplain (Junker 2004) algorithm to our setting to provide a trade-off between size and time. Experimental evaluations on standard benchmarks demonstrate significant improvements on both metrics, e.g., a size reduction of 38% on the GTSRB dataset and a time reduction of 90% on MNIST. We also explore applications of our verified explanations and show that explanation size is a useful proxy for both incorrectness detection and out-of-distribution detection.