Neural Network Verification for Gliding Drone Control: A Case Study

As machine learning is increasingly deployed in autonomous systems, verification of neural network controllers is becoming an active research domain. Existing tools and annual verification competitions suggest that soon this technology will become effective for real-world applications. Our application comes from the emerging field of microflyers that are passively transported by the wind, which may have various uses in weather or pollution monitoring. Specifically, we investigate centimetre-scale bio-inspired gliding drones that resemble Alsomitra macrocarpa diaspores. In this paper, we propose a new case study on verifying Alsomitra-inspired drones with neural network controllers, with the aim of adhering closely to a target trajectory. We show that our system differs substantially from existing VNN and ARCH competition benchmarks, and show that a combination of tools holds promise for verifying such systems in the future, if certain shortcomings can be overcome. We propose a novel method for robust training of regression networks, and investigate formalisations of this case study in Vehicle and CORA. Our verification results suggest that the investigated training methods do improve performance and robustness of neural network controllers in this application, but are limited in scope and usefulness. This is due to systematic limitations of both Vehicle and CORA, and the complexity of our system reducing the scale of reachability, which we investigate in detail. If these limitations can be overcome, it will enable engineers to develop safe and robust technologies that improve people's lives and reduce our impact on the environment.

A Generalised Framework for Property-Driven Machine Learning

Neural networks have been shown to frequently fail to satisfy critical safety and correctness properties after training, highlighting the pressing need for training methods that incorporate such properties directly. While adversarial training can be used to improve robustness to small perturbations within $\epsilon$-cubes, domains other than computer vision -- such as control systems and natural language processing -- may require more flexible input region specifications via generalised hyper-rectangles. Meanwhile, differentiable logics offer a way to encode arbitrary logical constraints as additional loss terms that guide the learning process towards satisfying these constraints. In this paper, we investigate how these two complementary approaches can be unified within a single framework for property-driven machine learning. We show that well-known properties from the literature are subcases of this general approach, and we demonstrate its practical effectiveness on a case study involving a neural network controller for a drone system. Our framework is publicly available at https://github.com/tflinkow/property-driven-ml.

Proof-Carrying Neuro-Symbolic Code

This invited paper introduces the concept of "proof-carrying neuro-symbolic code" and explains its meaning and value, from both the "neural" and the "symbolic" perspectives. The talk outlines the first successes and challenges that this new area of research faces.

Neural Network Verification is a Programming Language Challenge

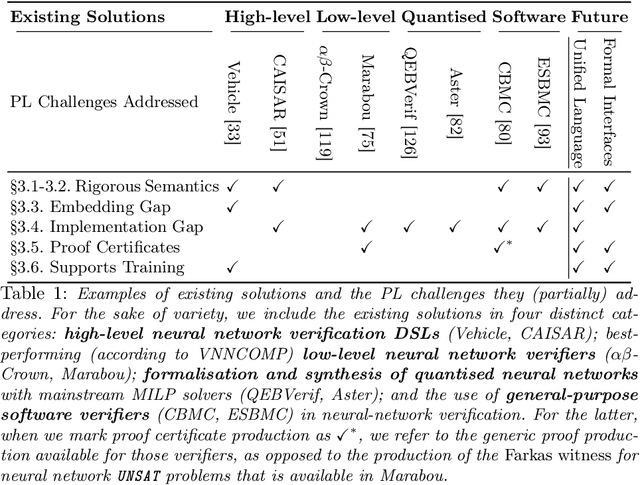
Neural network verification is a new and rapidly developing field of research. So far, the main priority has been establishing efficient verification algorithms and tools, while proper support from the programming language perspective has been considered secondary or unimportant. Yet, there is mounting evidence that insights from the programming language community may make a difference in the future development of this domain. In this paper, we formulate neural network verification challenges as programming language challenges and suggest possible future solutions.

A Neurosymbolic Framework for Bias Correction in CNNs

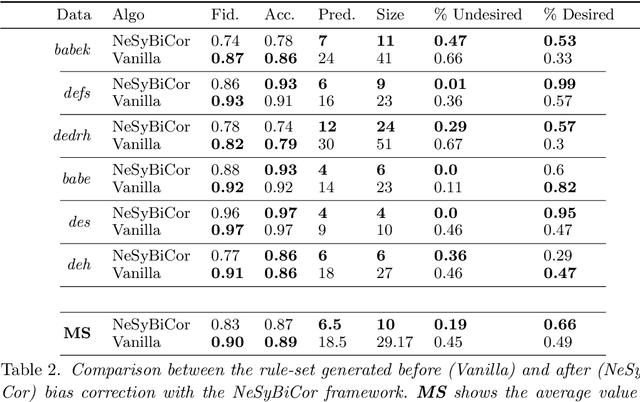
Recent efforts in interpreting Convolutional Neural Networks (CNNs) focus on translating the activation of CNN filters into stratified Answer Set Programming (ASP) rule-sets. The CNN filters are known to capture high-level image concepts, thus the predicates in the rule-set are mapped to the concept that their corresponding filter represents. Hence, the rule-set effectively exemplifies the decision-making process of the CNN in terms of the concepts that it learns for any image classification task. These rule-sets help expose and understand the biases in CNNs, although correcting the biases effectively remains a challenge. We introduce a neurosymbolic framework called NeSyBiCor for bias correction in a trained CNN. Given symbolic concepts that the CNN is biased towards, expressed as ASP constraints, we convert the undesirable and desirable concepts to their corresponding vector representations. Then, the CNN is retrained using our novel semantic similarity loss that pushes the filters away from the representations of concepts that are undesirable while pushing them closer to the concepts that are desirable. The final ASP rule-set obtained after retraining, satisfies the constraints to a high degree, thus showing the revision in the knowledge of the CNN for the image classification task. We demonstrate that our NeSyBiCor framework successfully corrects the biases of CNNs trained with subsets of classes from the Places dataset while sacrificing minimal accuracy and improving interpretability, by greatly decreasing the size of the final bias-corrected rule-set w.r.t. the initial rule-set.

A Certified Proof Checker for Deep Neural Network Verification

Recent advances in the verification of deep neural networks (DNNs) have opened the way for broader usage of DNN verification technology in many application areas, including safety-critical ones. DNN verifiers are themselves complex programs that have been shown to be susceptible to errors and imprecisions; this in turn has raised the question of trust in DNN verifiers. One prominent attempt to address this issue is enhancing DNN verifiers with the capability of producing proofs of their results that are subject to independent algorithmic certification (proof checking). Formulations of proof production and proof checking already exist on top of the state-of-the-art Marabou DNN verifier. The native implementation of the proof checking algorithm for Marabou was done in C++ and itself raised the question of trust in the code (e.g., in the precision of floating point calculations or guarantees for implementation soundness). Here, we present an alternative implementation of the Marabou proof checking algorithm in Imandra -- an industrial functional programming language and prover -- that allows us to obtain an implementation with formal guarantees, including proofs of mathematical results underlying the algorithm, such as the use of the Farkas lemma.

NLP Verification: Towards a General Methodology for Certifying Robustness

Deep neural networks have exhibited substantial success in the field of Natural Language Processing (NLP) and ensuring their safety and reliability is crucial: there are safety critical contexts where such models must be robust to variability or attack, and give guarantees over their output. Unlike Computer Vision, NLP lacks a unified verification methodology and, despite recent advancements in literature, they are often light on the pragmatical issues of NLP verification. In this paper, we make an attempt to distil and evaluate general components of an NLP verification pipeline, that emerges from the progress in the field to date. Our contributions are two-fold. Firstly, we give a general characterisation of verifiable subspaces that result from embedding sentences into continuous spaces. We identify, and give an effective method to deal with, the technical challenge of semantic generalisability of verified subspaces; and propose it as a standard metric in the NLP verification pipelines (alongside with the standard metrics of model accuracy and model verifiability). Secondly, we propose a general methodology to analyse the effect of the embedding gap, a problem that refers to the discrepancy between verification of geometric subpspaces on the one hand, and semantic meaning of sentences which the geometric subspaces are supposed to represent, on the other hand. In extreme cases, poor choices in embedding of sentences may invalidate verification results. We propose a number of practical NLP methods that can help to identify the effects of the embedding gap; and in particular we propose the metric of falsifiability of semantic subpspaces as another fundamental metric to be reported as part of the NLP verification pipeline. We believe that together these general principles pave the way towards a more consolidated and effective development of this new domain.

Marabou 2.0: A Versatile Formal Analyzer of Neural Networks

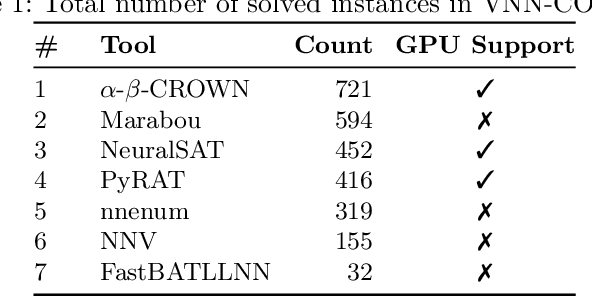
This paper serves as a comprehensive system description of version 2.0 of the Marabou framework for formal analysis of neural networks. We discuss the tool's architectural design and highlight the major features and components introduced since its initial release.

Vehicle: Bridging the Embedding Gap in the Verification of Neuro-Symbolic Programs

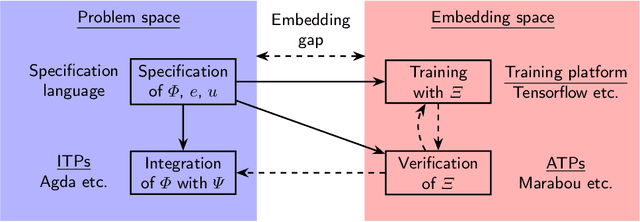
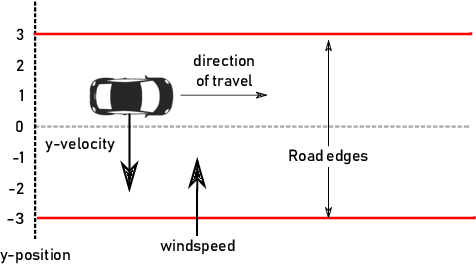
Neuro-symbolic programs -- programs containing both machine learning components and traditional symbolic code -- are becoming increasingly widespread. However, we believe that there is still a lack of a general methodology for verifying these programs whose correctness depends on the behaviour of the machine learning components. In this paper, we identify the ``embedding gap'' -- the lack of techniques for linking semantically-meaningful ``problem-space'' properties to equivalent ``embedding-space'' properties -- as one of the key issues, and describe Vehicle, a tool designed to facilitate the end-to-end verification of neural-symbolic programs in a modular fashion. Vehicle provides a convenient language for specifying ``problem-space'' properties of neural networks and declaring their relationship to the ``embedding-space", and a powerful compiler that automates interpretation of these properties in the language of a chosen machine-learning training environment, neural network verifier, and interactive theorem prover. We demonstrate Vehicle's utility by using it to formally verify the safety of a simple autonomous car equipped with a neural network controller.

Towards a Certified Proof Checker for Deep Neural Network Verification

Recent developments in deep neural networks (DNNs) have led to their adoption in safety-critical systems, which in turn has heightened the need for guaranteeing their safety. These safety properties of DNNs can be proven using tools developed by the verification community. However, these tools are themselves prone to implementation bugs and numerical stability problems, which make their reliability questionable. To overcome this, some verifiers produce proofs of their results which can be checked by a trusted checker. In this work, we present a novel implementation of a proof checker for DNN verification. It improves on existing implementations by offering numerical stability and greater verifiability. To achieve this, we leverage two key capabilities of Imandra, an industrial theorem prover: its support of infinite precision real arithmetic and its formal verification infrastructure. So far, we have implemented a proof checker in Imandra, specified its correctness properties and started to verify the checker's compliance with them. Our ongoing work focuses on completing the formal verification of the checker and further optimizing its performance.