Vehicle: Bridging the Embedding Gap in the Verification of Neuro-Symbolic Programs

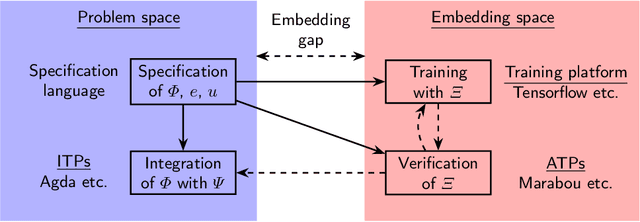
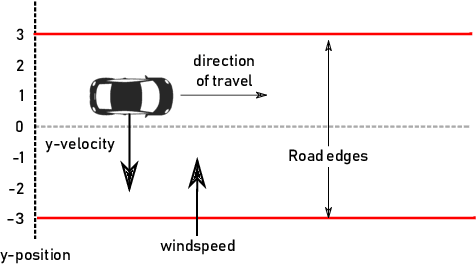
Neuro-symbolic programs -- programs containing both machine learning components and traditional symbolic code -- are becoming increasingly widespread. However, we believe that there is still a lack of a general methodology for verifying these programs whose correctness depends on the behaviour of the machine learning components. In this paper, we identify the ``embedding gap'' -- the lack of techniques for linking semantically-meaningful ``problem-space'' properties to equivalent ``embedding-space'' properties -- as one of the key issues, and describe Vehicle, a tool designed to facilitate the end-to-end verification of neural-symbolic programs in a modular fashion. Vehicle provides a convenient language for specifying ``problem-space'' properties of neural networks and declaring their relationship to the ``embedding-space", and a powerful compiler that automates interpretation of these properties in the language of a chosen machine-learning training environment, neural network verifier, and interactive theorem prover. We demonstrate Vehicle's utility by using it to formally verify the safety of a simple autonomous car equipped with a neural network controller.

Differentiable Logics for Neural Network Training and Verification

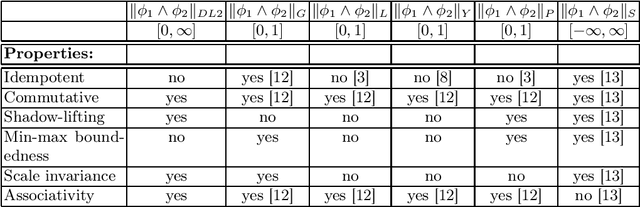
The rising popularity of neural networks (NNs) in recent years and their increasing prevalence in real-world applications have drawn attention to the importance of their verification. While verification is known to be computationally difficult theoretically, many techniques have been proposed for solving it in practice. It has been observed in the literature that by default neural networks rarely satisfy logical constraints that we want to verify. A good course of action is to train the given NN to satisfy said constraint prior to verifying them. This idea is sometimes referred to as continuous verification, referring to the loop between training and verification. Usually training with constraints is implemented by specifying a translation for a given formal logic language into loss functions. These loss functions are then used to train neural networks. Because for training purposes these functions need to be differentiable, these translations are called differentiable logics (DL). This raises several research questions. What kind of differentiable logics are possible? What difference does a specific choice of DL make in the context of continuous verification? What are the desirable criteria for a DL viewed from the point of view of the resulting loss function? In this extended abstract we will discuss and answer these questions.